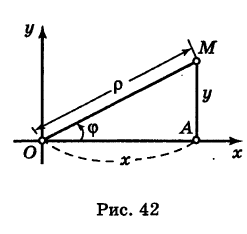
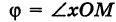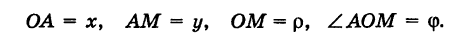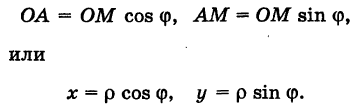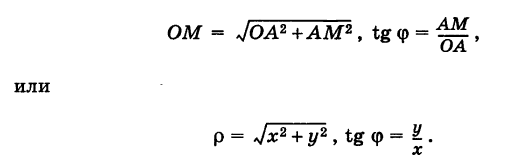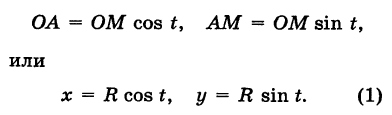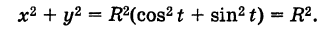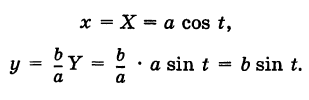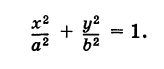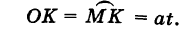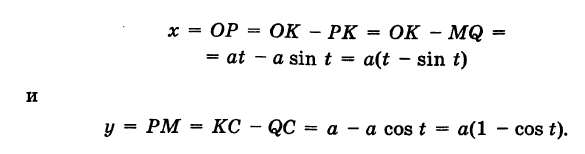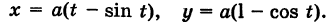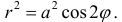Что такое полярная система координат

Полярная система координат: основные понятия и примеры

Полярная система координат: основные понятия и обозначения

Если уж речь зашла о полярной системе координат, то вообразите себя полярниками, стоящими на Северном полюсе. Или на Южном (это не так важно). Пусть в точке полюса находится начало линейки. В точку полюса также положим начало карандаша, а весь карандаш полностью прилегает к линейке. Теперь повернём карандаш так, чтобы его начало оставалось там же, на полюсе, а между ним и линейкой образовался некоторый угол поворота. Конец карандаша оказался в некоторой точке, назовём её M. Вот мы и получили полярные координаты точки M: длина карандаша и угол, на который был повёрнут карандаш. А теперь об этом же в более строгих и точных определениях.

Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Связь полярных координат с декартововыми координатами

Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда

Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

.

Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка M, и, кроме того, воспользоваться тем, что тангенс угла φ равен .

Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.

Задачи о точках в полярной системе координат

Пример 1. В полярной системе координат на плоскости даны точки

Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.

Пример 2. В полярной системе координат на плоскости даны точки

Найти полярные координаты точек, симметричных этим точкам относительно полюса.

Пример 3. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки

Найти декартовы координаты этих точек.

Решение. Используем формулы перехода от полярных координат к декартовым:

Получаем следующие декартовы координаты данных точек:

Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки

Найти полярные координаты этих точек.

Источник

Полярная система координат (полярные координаты)

— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат <связанную с данной прямоугольной).

Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

Пример 2.9. В полярной системе координат :

а) изобразить координатные линии ;

Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии и — полупрямые (рис.2.30,а).

2. Расстояние между двумя точками и (длина отрезка ) вычисляется по формуле

что следует из теоремы косинусов (рис.2.31).

Она положительна, если (при этом ориентация пары радиус- векторов и правая), и отрицательна, если \varphi_2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEcAAAASBAMAAAD73d5oAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAwPxBoV0BgTEhELHR4JFxAbyQhgAAASJJREFUKM9jYCAdsEYRoyqmCqvwUgYGa1E4jy3mJczQCQzLRRZAOY8ZWBUPTUCoCvSEMGYzcJ0VcoCwOQUY1jZwFyAZbegBppwZ+Bw41CBC/AFALjuyIgZrCZCJxxgmMjBAFTFO4NrAwGLAwIlQNAWkiNkB6BCgNcYgZzE2sAYw9CSYX0cYJJwAVsQmwMAdsO7LDSCHbxt3A8dlhpniMIdDncSlwbGB7SHDbwZHEOdskalTAAMDTFEM1HMMnxyda6UYPjEUgThLlJRAeqGK4MHEwHpJ6T6I9gHzvNsY4IpYkQK8yQrkNg4NMEefAaEIGXwCqWFY2ADWrIxD0UGw+yVYQRS7Gg5FYBv4gq3B8QKONzvdSnRFBmA7lRQJJx22NKDLACxqN6Lf3w5xAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> (ориентация пары радиус-векторов и левая).

Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:

а) скалярное произведение ;

в) внешнее произведение ;

г) площадь треугольника ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

д) По формулам (2.17) находим прямоугольные координаты точек и :

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

так как точка лежит в четверти.

б) При инверсии относительно окружности радиуса полярные координаты образа выражаются через полярные координаты прообраза следующими формулами:

Поэтому, учитывая пункт «а», находим (для ):

Источник

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

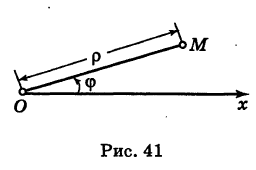
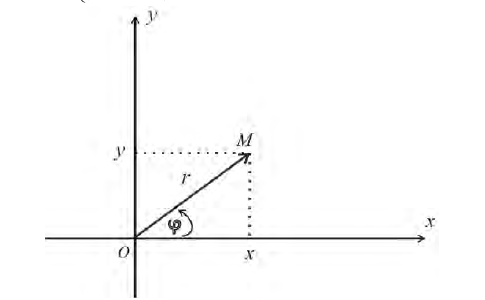
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

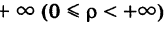
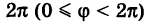
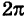
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

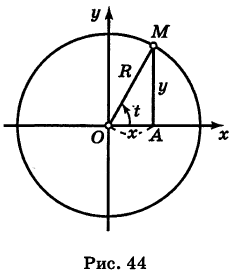
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

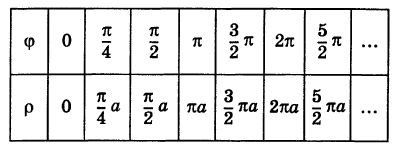
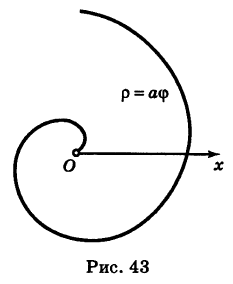
Рассмотрим кривую 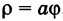, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 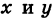, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М 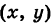— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

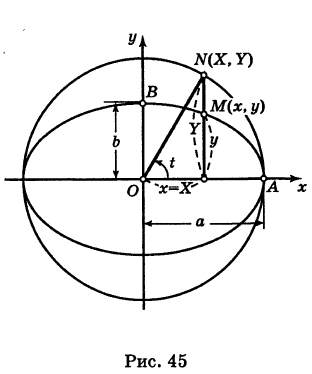
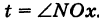
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

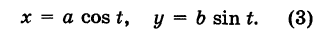
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

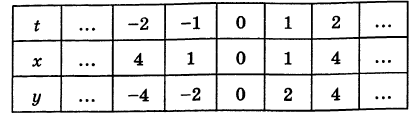
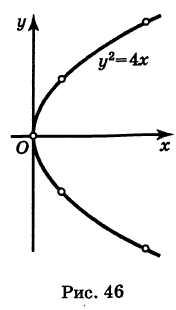
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 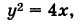т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

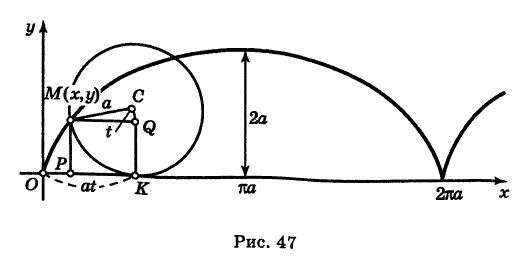
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

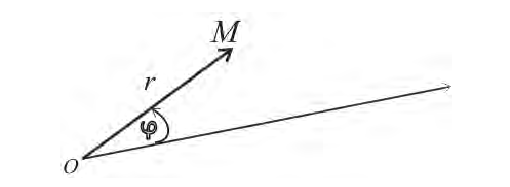
Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
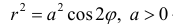
Решение.

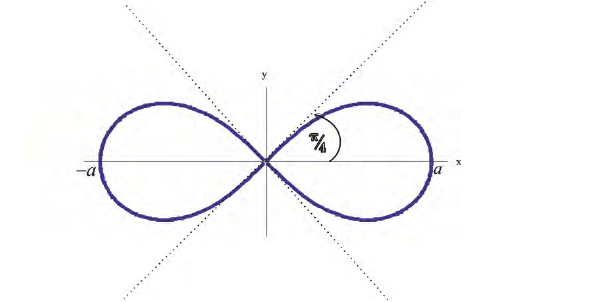
Рис.3. Лемниската

Пример 2.

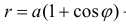
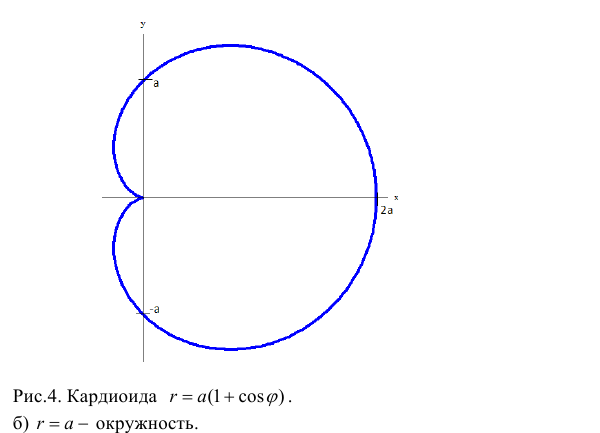
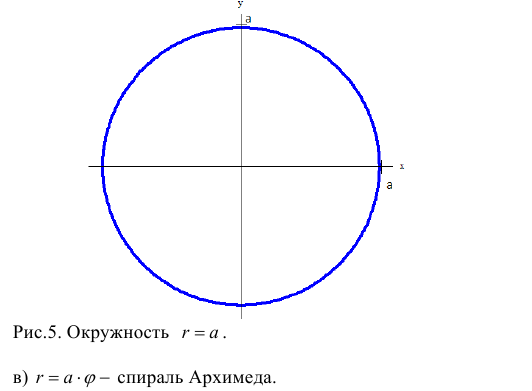
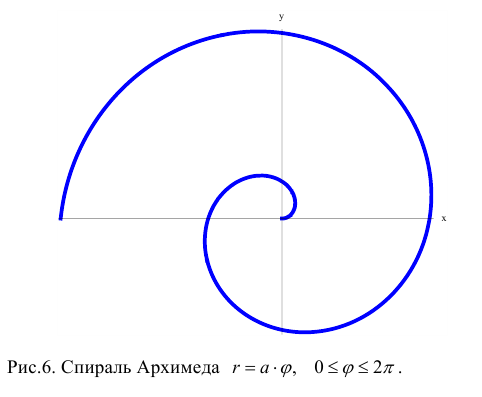
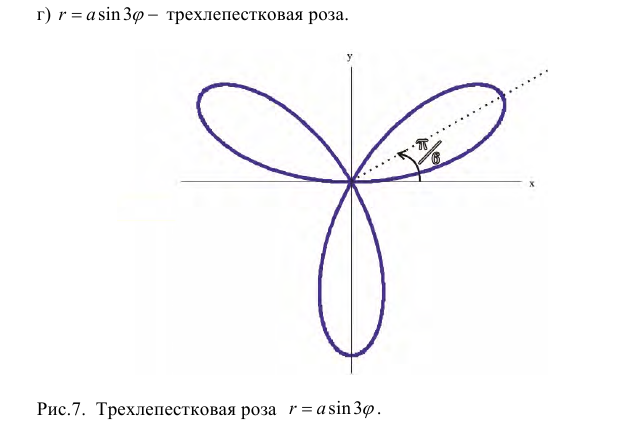
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

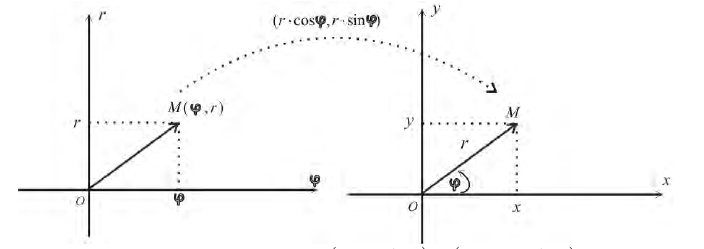
При этом, если r > 0, то векторы 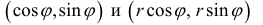сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Грегуар де Сент-Винсент и Бонавентура Кавальери независимо представил эти концепции в середине 17 века, хотя сам термин полярные координаты был приписан Грегорио Фонтана в 18 веке. Первоначальной мотивацией к введению полярной системы было изучение круговой и орбитальное движение.

Полярные координаты наиболее подходят в любом контексте, где рассматриваемое явление по своей природе привязано к направлению и длине от центральной точки на плоскости, например спирали. Плоские физические системы с телами, движущимися вокруг центральной точки, или явлениями, происходящими из центральной точки, часто проще и интуитивно моделировать с использованием полярных координат.

Полярная система координат расширяется до трех измерений двумя способами: цилиндрический и сферический системы координат.

Содержание

История

Понятия угла и радиуса использовались еще древними народами первого тысячелетия. до н.э. В Греческий астроном и астролог Гиппарх (190–120 гг. До н.э.) создал таблицу аккорд функции, задающие длину хорды для каждого угла, и есть ссылки на его использование полярных координат при установлении положения звезд. [2] В На спиралях, Архимед описывает Архимедова спираль, функция, радиус которой зависит от угла. Однако греческая работа не охватывала полную систему координат.

Существуют различные версии введения полярных координат как части формальной системы координат. Полная история предмета описана в Гарвард профессор Джулиан Лоуэлл Кулиджс Происхождение полярных координат. [5] Грегуар де Сент-Винсент и Бонавентура Кавальери независимо ввел эти понятия в середине семнадцатого века. Сент-Винсент писал о них в частном порядке в 1625 году и опубликовал свою работу в 1647 году, а Кавальери опубликовал свою работу в 1635 году с исправленной версией, появившейся в 1653 году. Кавальери сначала использовал полярные координаты для решения проблемы, относящейся к области в пределах Архимедова спираль. Блез Паскаль впоследствии использовали полярные координаты для расчета длины параболические дуги.

В Метод флюсий (написано в 1671 году, опубликовано в 1736 году), сэр Исаак Ньютон исследовал преобразования между полярными координатами, которые он назвал «Седьмой манер; для спиралей», и девятью другими системами координат. [6] В журнале Acta Eruditorum (1691), Джейкоб Бернулли использовали систему с точкой на линии, называемую столб и полярная ось соответственно. Координаты задавались расстоянием от полюса и углом от полюса. полярная ось. Работа Бернулли распространилась на поиск радиус кривизны кривых, выраженных в этих координатах.

Фактический срок полярные координаты был приписан Грегорио Фонтана и использовался итальянскими писателями 18 века. Термин появился в английский в Джордж Пикокперевод 1816 года Лакруас Дифференциальное и интегральное исчисление. [7] [8] Алексис Клеро был первым, кто придумал полярные координаты в трех измерениях, и Леонард Эйлер был первым, кто их действительно разработал. [5]

Конвенции

Углы в полярных обозначениях обычно выражаются либо градусы или же радианы (2 π рад, равный 360 °). Градусы традиционно используются в навигация, геодезия, и многие прикладные дисциплины, а радианы чаще встречаются в математике и математике. физика. [9]

Угол φ определяется, чтобы начать с 0 ° от справочное направление, и увеличиваться для вращений в любом против часовой стрелки (против часовой стрелки) или же по часовой стрелке (cw) ориентация. Так, например, в математике, контрольное направление обычно рисуется как луч от полюса по горизонтали вправо, а полярный угол увеличивается до положительных углов при вращении против часовой стрелки, тогда как в навигации (несущий, Заголовок) направление 0 ° направлено вертикально вверх, и угол увеличивается при вращении по часовой стрелке. Полярные углы уменьшаются в сторону отрицательных значений для вращений в противоположных направлениях.

Уникальность полярных координат

Преобразование между полярными и декартовыми координатами

Полярные координаты р и φ можно преобразовать в Декартовы координаты Икс и у используя тригонометрические функции синус и косинус:

куда atan2 это обычная вариация на арктангенс функция определяется как

Если р сначала рассчитывается, как указано выше, затем эта формула для φ можно сказать немного проще, используя стандарт арккозин функция:

Значение φ выше это основная стоимость функции комплексного числа аргумент применительно к Икс + иу. Угол в диапазоне [0, 2 π ) можно получить добавлением 2 π к значению, если оно отрицательное (другими словами, когда у отрицательный).

Полярное уравнение кривой

Уравнение, определяющее алгебраическая кривая выраженный в полярных координатах, известен как полярное уравнение. Во многих случаях такое уравнение можно просто задать, задав р как функция из φ. Полученная кривая будет состоять из точек вида (р(φ), φ) и может рассматриваться как график полярной функции р. Обратите внимание, что, в отличие от декартовых координат, независимая переменная φ это второй вход в заказанную пару.

Из-за круговой природы полярной системы координат многие кривые могут быть описаны довольно простым полярным уравнением, тогда как их декартова форма намного сложнее. К наиболее известным из этих кривых относятся полярная роза, Архимедова спираль, лемниската, Limaçon, и кардиоидный.

Для круга, линии и полярной розы ниже подразумевается, что нет ограничений на область и диапазон кривой.

Это можно упростить различными способами для соответствия более конкретным случаям, таким как уравнение

для круга с центром на полюсе и радиусом а. [14]

решение со знаком минус перед квадратным корнем дает ту же кривую.

Линия

Радиальный линии (проходящие через полюс) представлены уравнением

Полярная роза

А полярная роза представляет собой математическую кривую, которая выглядит как цветок с лепестками и может быть выражена простым полярным уравнением,

для любой постоянной γ₀ (в том числе 0). Если k является целым числом, эти уравнения дадут kлепестковая роза, если k является странный, или 2kлепестковая роза, если k даже. Если k является рациональным, но не целым числом, может образоваться роза, но с перекрывающимися лепестками. Обратите внимание, что эти уравнения никогда не определяют розу с 2, 6, 10, 14 и т. Д. Лепестками. В Переменная а непосредственно представляет длину или амплитуду лепестков розы, а k относится к их пространственной частоте. Постоянная γ₀ можно рассматривать как фазовый угол.

Архимедова спираль

В Архимедова спираль это спираль, которая была открыта Архимед, которое также можно выразить в виде простого полярного уравнения. Он представлен уравнением

Конические секции

А коническая секция с одним фокусом на полюсе, а другой где-то на луче 0 ° (так что большая ось лежит вдоль полярной оси) определяется выражением:

р = ℓ 1 − е потому что ⁡ φ >>

Пересечение двух полярных кривых

Сложные числа

Каждый комплексное число можно представить в виде точки на комплексная плоскость, и поэтому может быть выражено указанием либо декартовых координат точки (называемых прямоугольной или декартовой формой), либо полярных координат точки (называемых полярной формой). Комплексное число z можно представить в прямоугольной форме как

куда я это мнимая единица, или, альтернативно, может быть записан в полярной форме (через приведенные формулы преобразования над) в качестве

куда е является Число Эйлера, которые эквивалентны, как показано Формула Эйлера. [15] (Обратите внимание, что эта формула, как и все те, которые включают экспоненты углов, предполагает, что угол φ выражается в радианы.) Для преобразования между прямоугольной и полярной формами комплексного числа приведенные формулы преобразования над может быть использован.

Для операций умножение, разделение, и возведение в степень Для комплексных чисел, как правило, гораздо проще работать с комплексными числами, выраженными в полярной форме, а не в прямоугольной. Из законов возведения в степень:

Исчисление

Исчисление может применяться к уравнениям, выраженным в полярных координатах. [16] [17]

Угловая координата φ В этом разделе выражается в радианах, что обычно используется при расчетах.

Дифференциальное исчисление

Следовательно, имеем следующие формулы:

Используя обратное преобразование координат, можно вывести аналогичное взаимное соотношение между производными. Учитывая функцию ты(р,φ), следует, что

Следовательно, мы имеем следующие формулы:

Чтобы найти декартовский наклон касательной к полярной кривой р(φ) в любой заданной точке, кривая сначала выражается как система параметрические уравнения.

Дифференцировать оба уравнения относительно φ дает

Разделив второе уравнение на первое, мы получим декартов наклон касательной к кривой в точке (р(φ), φ) :

Для других полезных формул, включая расходимость, градиент и лапласиан в полярных координатах, см. криволинейные координаты.

Интегральное исчисление (длина дуги)

Интегральное исчисление (площадь)

Следовательно, общая площадь всех секторов равна

Обобщение

С помощью Декартовы координаты, бесконечно малый элемент площади можно вычислить как dA = dx dy. В правило замены для кратных интегралов заявляет, что при использовании других координат Якобиан Необходимо учитывать определитель формулы преобразования координат:

Следовательно, элемент площади в полярных координатах можно записать как

Теперь функцию, заданную в полярных координатах, можно проинтегрировать следующим образом:

Здесь, р это та же область, что и выше, а именно область, ограниченная кривой р(ϕ) и лучи φ = а и φ = б. Формула для площади р упомянутое выше можно получить, взяв ж тождественно равно 1.

Более удивительное применение этого результата дает Гауссов интеграл, здесь обозначено K:

Векторное исчисление

Определим единичные векторы

в плоскости движения, перпендикулярной радиальному направлению, где k ^ >>> — единичный вектор, нормальный к плоскости движения.

Центробежные и кориолисовы термины

Период, термин р φ ˙ 2 > ^ <2>> иногда называют центростремительное ускорение, а срок 2 р ˙ φ ˙ > <точка >> как Кориолисовое ускорение. Например, см. Шанкар. [18]

Примечание: эти члены, которые появляются, когда ускорение выражается в полярных координатах, являются математическим следствием дифференцирования; они появляются всякий раз, когда используются полярные координаты. В динамике планарных частиц эти ускорения появляются при настройке Ньютона. второй закон движения во вращающейся системе отсчета. Здесь эти дополнительные термины часто называют фиктивные силы; фиктивны, потому что они просто результат изменения системы координат. Это не значит, что их не существует, скорее они существуют только во вращающейся рамке.

Совместно вращающаяся рама

где над точками обозначены временные дифференциации, а F это чистая реальная сила (в отличие от фиктивных сил). С точки зрения компонентов это векторное уравнение принимает следующий вид:

которые можно сравнить с уравнениями для инерциальной системы отсчета:

Для общего движения частицы (в отличие от простого кругового движения) центробежные силы и силы Кориолиса в системе отсчета частицы обычно называют мгновенными. соприкасающийся круг его движения, а не к фиксированному центру полярных координат. Подробнее см. центростремительная сила.

Дифференциальная геометрия

В современной терминологии дифференциальная геометрия, полярные координаты обеспечивают карты координат для дифференцируемое многообразие ℝ 2 <(0,0)>, плоскость минус начало координат. В этих координатах евклидова метрический тензор дан кем-то

Расширения в 3D

Полярная система координат расширена до трех измерений с двумя разными системами координат: цилиндрический и сферическая система координат.

Приложения

Положение и навигация

Полярные координаты часто используются в навигация в качестве пункта назначения или направления движения можно указать угол и расстояние до рассматриваемого объекта. Например, самолет используйте для навигации слегка измененную версию полярных координат. В этой системе, обычно используемой для любого вида навигации, луч 0 ° обычно называется курсом 360, а углы продолжаются в по часовой стрелке направление, а не против часовой стрелки, как в математической системе. Заголовок 360 соответствует магнитный север, а заголовки 90, 180 и 270 соответствуют магнитному востоку, югу и западу соответственно. [20] Таким образом, самолет, летящий в 5 морских милях на восток, будет лететь на 5 единиц по курсу 90 (читать ноль-девять-ноль к управления воздушным движением). [21]

Моделирование

Отображение систем радиальная симметрия обеспечивают естественные настройки для полярной системы координат, при этом центральная точка действует как полюс. Ярким примером такого использования является уравнение потока грунтовых вод применительно к радиально-симметричным скважинам. Системы с радиальная сила также хорошие кандидаты для использования полярной системы координат. Эти системы включают гравитационные поля, которые подчиняются закон обратных квадратов, а также системы с точечные источники, Такие как радиоантенны.

Радиально-асимметричные системы также можно моделировать с помощью полярных координат. Например, микрофонс образец пикапа иллюстрирует его пропорциональную реакцию на входящий звук с заданного направления, и эти шаблоны могут быть представлены в виде полярных кривых. Кривая для стандартного кардиоидного микрофона, наиболее распространенного однонаправленного микрофона, может быть представлена ​​как р = 0,5 + 0,5 дюйма (ϕ) на целевой проектной частоте. [22] На более низких частотах картина смещается в сторону всенаправленности.

Источник