Что такое попарно пересекающиеся прямые определение
Научная электронная библиотека
Пиралова О. Ф., Ведякин Ф. Ф.,
3.4. Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
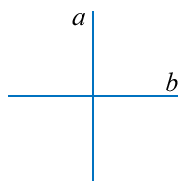
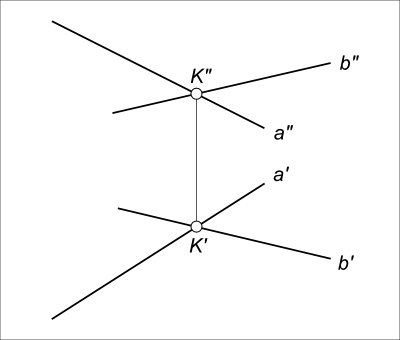
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
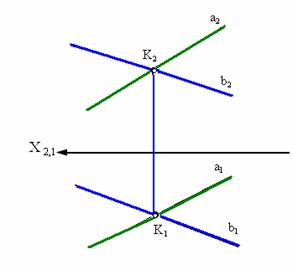
Рис. 3.4. Пересекающиеся прямые
2. Параллельные прямые
На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).
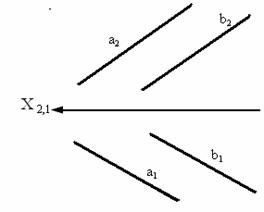
Рис. 3.5. Изображение параллельных прямых
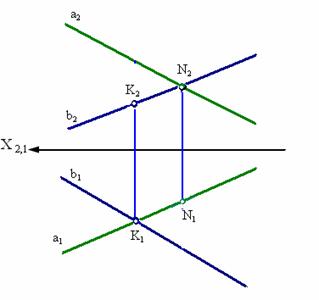
Пересекающиеся прямые
Пересекающиеся прямые — это в евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений.
Содержание:
Понятие пересекающихся прямых
Определение. Если две прямые имеют только одну общую точку, то такие прямые называют пересекающимися.
На рисунке 2.291 прямые 
Можно доказать такую теорему.
Теорема 1. Через две пересекающиеся прямые можно провести плоскость, и только одну.
Несколько прямых могут пересекаться не в одной точке, а, например, попарно. На рисунке 2.292 изображено пересечение трех прямых, каждые две из которых пересекаются только в одной точке. При этом образуется треугольник и вся эта фигура всегда лежит в одной плоскости.
Четыре прямые, каждые две из которых имеют только одну общую точку, образуют четырехугольник (рис. 2.293).
На рисунках 2.294, 2.295 изображены куб и тетраэдр, у которых продолжены их ребра. Мы видим, что в каждой вершине куба и тетраэдра пересекаются три прямые.
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые?
Сразу говорю, что задачу решать НЕ НАДО. Оставьте это мне. Я просто хочу разобраться, что означает «попарное пересекающиеся прямые».
У меня есть такая интерпретация: Имеется в виду, что все прямые «собраны» в пары. И каждая такая «сладкая парочка» пересекается другой такой же парой или «одиночной» прямой. Правда в этом конкретном случае «одиночек» нет, ибо количество прямых четное.
Я правильно все понимаю, или моя интерпретация неверна? Если неверна, то что тогда имеется в виду?
задан 23 Май ’13 13:26
I_Robot
183 ● 4 ● 17 ● 38
92% принятых
Здесь имеется в виду, что какие бы две прямые из четырёх мы ни взяли, они будут пересекаться.
«они будут пересекаться.» Может быть, более точным будет сказать «они ДОЛЖНЫ пересекаться»?
Кстати, преобразуйте пожалуйста свой комментарий в ответ, дабы я мог закрыть вопрос.
3 ответа
Можно сказать «они пересекаются», «они должны пересекаться», «они будут пересекаться». Это всё одна и та же мысль. Суть в том, что любые две прямые из четырёх имеют точку пересечения. Фактически, это означает, что среди прямых нет параллельных (хотя в принципе такие прямые могли бы быть в какой-то другой ситуации, и тогда ответ был бы другим). Слово «попарно» вообще очень часто используется в математике. Например, «даны три попарно различных числа». Это значит, что первое число не равно второму, а также не равно третьему, а второе число не равно третьему.
отвечен 23 Май ’13 13:57
Если речь идет об одной паре прямых, то в одной точке, а ежели о двух парах и более, то рассматриваютя разные варианты расположения уже самих пересекающихся пар прямых.
отвечен 13 Сен ’15 13:02
Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?
отвечен 22 Сен ’17 19:18
Здравствуйте
Пересекающиеся прямые
Если две прямые имеют общую точку, то говорят, что эти прямые пересекаются. Такие прямые называют пересекающимися прямыми:
Точка пересечения — это точка, общая для двух или более геометрических фигур.
Перпендикуляр и наклонная
При пересечении вертикальной и горизонтальной прямой линии образуется четыре прямых угла. Такие линии, относительно друг к другу, называются перпендикулярными линиями или просто перпендикулярами:
Даже если прямые не являются вертикальной и горизонтальной линиями, но при пересечении образуют четыре прямых угла, то они всё равно являются перпендикулярными:
Если прямая линия пересекает другую не под прямым углом, то такая линия называется наклонной к прямой, которую она пересекает. При этом образуется четыре угла: два из них будут острыми и два тупыми:
Образованные острые углы равны и относительно друг друга будут называться вертикальными углами. То же самое можно сказать и об образованных тупых углах — они равные и вертикальные.
Пересекающиеся прямые
Так как проекция прямой есть прямая, то проекцией пересекающихся прямых будут их пересекающиеся проекции:
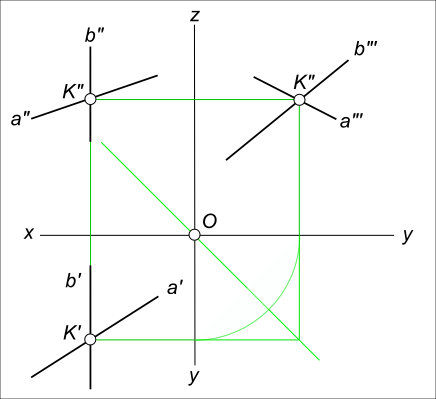
Чтобы определить на эпюре (комплексном чертеже), пересекаются ли данные прямые в пространстве, достаточно провести линию связи из одной точки пересечения проекций к другой. Если проекции точки пересечения прямых будут лежать на одной линии связи, то прямые пересекаются. Чтобы построить на эпюре (комплексном чертеже), пересекающиеся прямые в пространстве, достаточно провести линию связи из одной точки пересечения проекций прямых к другой. Проекцию точки пересечения прямых на другой плоскости проекций находим в пересечении линии проекционной связи, с проекцией одной из пересекающихся прямых, через нее проводим проекцию другой прямой. Если одна из прямых параллельна профильной плоскости проекций, то для определения положения точки пересечения прямых в пространстве необходимо построить третью (профильную) проекцию.
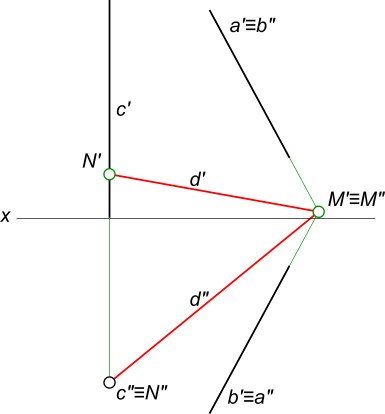
Построить проекции прямой d, пересекающей заданные прямые a, b и c
Продолжив проекции прямых a и b находим M` =a` ∩ b` и M»=a» ∩ b» проекции точки M, которые совпадают а поэтому находятся на одной линии проекционной связи и следовательно a и b пересекающиеся прямые. Через точку M пересечения прямых a, b и прямую c проводим прямую d(d`, d»): M=a ∩ b; N`= c` ∩ d` ^ N»= c» ∩ d»; N ∈ d ^ M ∈ d