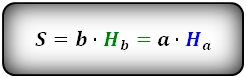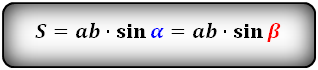Что такое попарно равны
Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
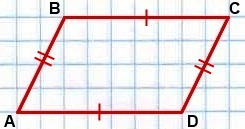
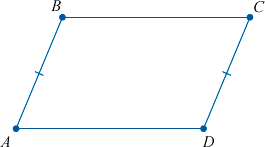
1. Противоположные стороны параллелограмма попарно равны
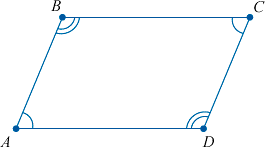
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
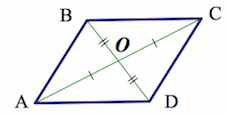
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали 
параллелограмма и стороны
связаны следующим соотношением: 
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник 
является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны: 
2. Противоположные углы попарно равны: 
3. Диагонали пересекаются и в точке пересечения делятся пополам
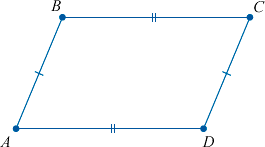
4. Противоположные стороны равны и параллельны: 
5. 
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
Формулы площади параллелограмма смотрите здесь.Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Значение слова «попарно»
ПОПА́РНО, нареч. По двое, парами. Лебеди прилетают почти всегда попарно. С. Аксаков, Записки ружейного охотника. [Солдаты] стояли попарно, в полной караульной форме. Катаев, Белеет парус одинокий.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ПОПА’РНО, нареч. По-двое, парами. Ученики шли п.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
попа́рно
1. по двое, парами ◆ Дамы входили большей частью попарно и становились вдоль стены. Апухтин, «Между жизнью и смертью», 1892 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова асбест (существительное):
Синонимы к слову «попарно»
Предложения со словом «попарно»
Цитаты из русской классики со словом «попарно»
Понятия, связанные со словом «попарно»
Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).
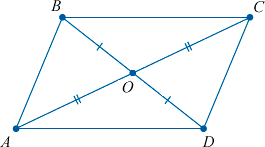
Если противоположные стороны четырехугольника попарно равны
Теорема (3-й признак параллелограмма).
Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
Дано: ABCD — четырехугольник,
Доказать: ABCD — параллелограмм.
1. Проведем диагональ AC.
2. Рассмотрим треугольники ABC и CDA (важно правильно назвать треугольники!)
3) сторона AC- общая
Следовательно, треугольники ABC и CDA равны (по трем сторонам).
3. Из равенства треугольников следует равенство соответствующих углов:
4. ∠CAB и∠ACD — внутренние накрест лежащие при прямых AB и CD и секущей AC.
Так как ∠CAB=∠ACD, то прямые параллельны: AB ∥ CD (по признаку параллельности прямых).
Аналогично, из равенства углов ∠ACB=∠CAD следует параллельность другой пары прямых: AD ∥ BC.
5. Доказали, что в четырехугольнике ABCD
Следовательно, ABCD — параллелограмм (по определению).
Что и требовалось доказать.
Можно не доказывать параллельность прямых AD и BC.
2) AB ∥ CD (по доказанному),
следует, что ABCD — параллелограмм (по 2-му признаку).
6 Comments
Спасибо, какой уже раз ваш сайт выручает.
Спасибо) Очень хороший сайт все по полочкам разложили)
В «Дано» опечатка: не AC=CD, а AB=BC
И я сам ошибся 🙂 AB=CD
Noob, спасибо! К сожалению, опечатки случаются.
Параллелограмм — это базовая геометрическая фигура с рядом важных свойств и признаков
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.
С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.
Определение параллелограмма
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.
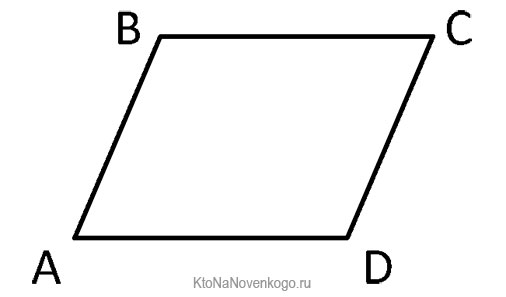
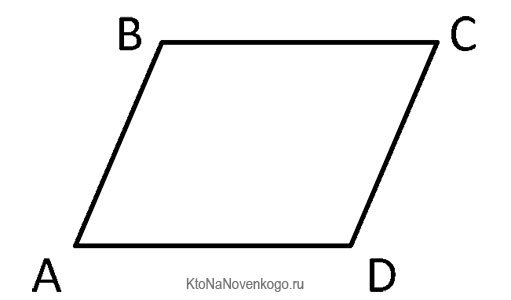
Выглядит эта фигура вот так:
Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.
Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.
Можно даже дать такие определения:
Происхождение термина «параллелограмм»
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.
Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».
Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.
Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.
Свойства и признаки параллелограмма
Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.
Возьмем в качестве примера еще раз нашу фигуру:
Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:
AD II BC и AD =BC. Или AB II CD и AB = CD
∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180
Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:
Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.
Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.
Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.
Как посчитать периметр параллелограмма
Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.
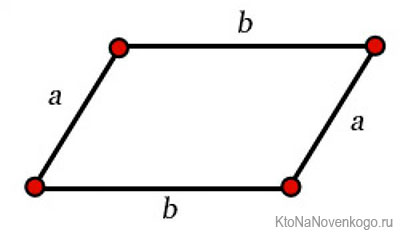
Снова возьмем для примера нашу фигуру:
Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:
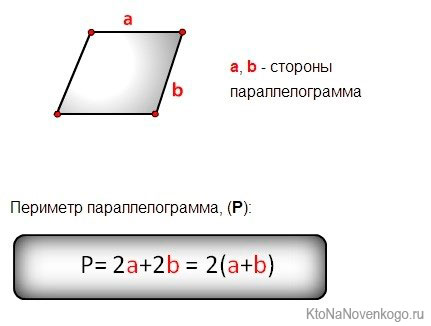
Чтобы рассчитать периметр, надо просто сложить все стороны:
Но эту же формулу можно переиначить и по-другому:
Это и есть формула периметра параллелограмма, которая записана во всех учебниках.
Как рассчитать площадь параллелограмма
С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.
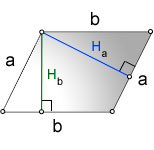
Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.
Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Сталкивалась с этим словом только в школе, на уроках геометрии, больше нигде 🙂
Что такое параллелограмм: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – параллелограмма.
Определение параллелограмма
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.
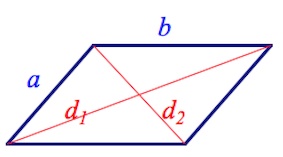
Обычно параллелограмм записывается путем перечисления четырех его вершин, например, ABCD. А пары параллельных сторон, чаще всего, обозначаются маленькими латинскими буквами, в нашем случае – a и b.
Частные случаи параллелограмма: квадрат, ромб и прямоугольник.
Свойства параллелограмма
Свойство 1
Противолежащие (или противоположные) стороны параллелограмма равны.
Свойство 2
Противолежащие углы параллелограмма равны.
Свойство 3
Сумма углов параллелограмма, прилежащих к одной стороне, равняется 180°.
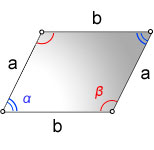
Для рисунка выше: α + β = 180°.
Свойство 4
Любая из двух диагоналей параллелограмма делит его на два равных треугольника.
Свойство 5
Диагонали параллелограмма в точке пересечения делятся пополам.
Свойство 6
Точка пересечения диагоналей параллелограмма (также называется центром симметрии) одновременно является точкой пересечения его средних линий.
Средняя линия четырехугольника – это отрезок, который соединяет середины его противоположных сторон.
В данном случае средние лини – это отрезки FM и EN.
Свойство 7
Угол между двумя высотами в параллелограмме равен его острому углу.
Свойство 8
Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны (т.е. расположены под углом 90° друг к другу).
Свойство 9
Биссектрисы двух противолежащих углов параллелограмма параллельны.
Углы ABC и ADC противолежащие. Их биссектрисы параллельны, т.е. BR || DP.
Свойство 10: тождество параллелограмма
Сумма квадратов диагоналей параллелограмма равняется удвоенной сумме квадратов его смежных сторон.
Признаки параллелограмма
Четырехугольник ABCD без самопересечений является параллелограммом, если для него справедливо одно из утверждений ниже: