Что такое попарные прямые

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

3.4. Взаимное положение прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.

Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).

.

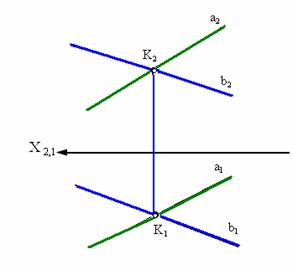
Рис. 3.4. Пересекающиеся прямые

2. Параллельные прямые

На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

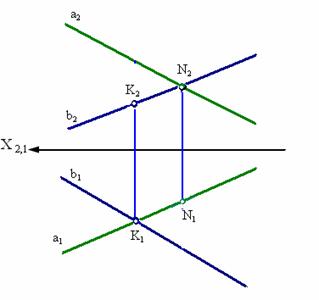
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.

На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

.

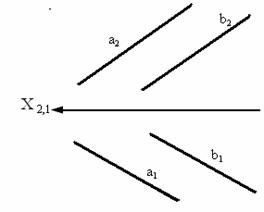
Рис. 3.5. Изображение параллельных прямых

.

Источник

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Пересекающиеся прямые

Пересекающиеся прямые — это в евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений.

Содержание:

Понятие пересекающихся прямых

Определение. Если две прямые имеют только одну общую точку, то такие прямые называют пересекающимися.

На рисунке 2.291 прямые пересекаются в точке О.

Можно доказать такую теорему.

Теорема 1. Через две пересекающиеся прямые можно провести плоскость, и только одну.

Несколько прямых могут пересекаться не в одной точке, а, например, попарно. На рисунке 2.292 изображено пересечение трех прямых, каждые две из которых пересекаются только в одной точке. При этом образуется треугольник и вся эта фигура всегда лежит в одной плоскости.

Четыре прямые, каждые две из которых имеют только одну общую точку, образуют четырехугольник (рис. 2.293).

На рисунках 2.294, 2.295 изображены куб и тетраэдр, у которых продолжены их ребра. Мы видим, что в каждой вершине куба и тетраэдра пересекаются три прямые.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Понятие скрещивающихся прямых

В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.

Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.

Существует теорема, представляющая собой признак скрещивающихся прямых.

Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.

Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;

2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;

3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.

Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:

Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.

Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.

Сонаправленные лучи

В планиметрии существует понятие сонаправленных лучей. Пусть на плос-ти есть два луча О₁А и О₂В. Проведем прямую О₁О₂. Она, как и всякая прямая, разделит плос-ть на две полуплоскости. Для того, чтобы лучи О₁А и О₂В считались сонаправленными, необходимо выполнение двух условий:

1) они должны оказаться в одной полуплоскости;

2) они должны быть параллельными.

Здесь мы рассмотрели случай, когда лучи О₁А и О₂В находятся на разных прямых. Возможен частный случай, когда они располагаются на одной прямой. В таком случае для сонаправленности лучей достаточно, чтобы один из них полностью лежал на другом:

Рассмотрим теорему, касающуюся сонаправленных лучей, причем она верна не только в планиметрии, но и в стереометрии.

В доказательстве сразу рассмотрим случай углов, располагающихся в разных плос-тях. Пусть есть углы О₁ и О₂, стороны которых образуют попарно сонаправленные лучи. На одной паре лучей отметим точки А₁ и А₂ так, чтобы отрезки О₁А₁ и О₂А₂ были одинаковыми. На другой паре лучей аналогично отложим точки В₁ и В₂ так, чтобы одинаковыми были отрезки О₁В₁ и О₂В₂:

Заметим, что лучи О₁А₁ и О₂А₂ как сонаправленные должны располагаться в одной плос-ти, иначе они не будут параллельными. Тогда О₁А₁А₂О₂ – плоский четырехугольник. Отрезки О₁А₁ и О₂А₂ параллельны и одинаковы. Это значит, что О₁А₁А₂О₂ – параллелограмм. Аналогично легко убедиться, что параллелограммом является и четырехугольник О₁В₁В₂О₂. Это значит, что

Отсюда вытекает (по свойству транзитивности), что отрезки А₁А₂ и В₁В₂ также одинаковы и параллельны, а потому А₁А₂В₂В₁ – также параллелограмм. Значит, стороны А₁В₁ и А₂В₂ одинаковы. Получается, что у ∆О₁А₁В₁ и ∆О₂А₂В₂ одинаковы все стороны, поэтому ∆О₁А₁В₁ и ∆О₂А₂В₂ равны. Отсюда вытекает и равенство углов ∠А₁О₁В₁ и ∠А₂О₂В₂, ч. т. д.

Угол между прямыми

Напомним, какая величина считается углом между пересекающимися прямыми. При пересечении прямых образуется 4 угла. Зная один из них, легко вычислить и остальные углы. Понятно, что хотя бы один из углов будет не превышать 90°. Именно такой угол и принимается за угол между прямыми:

Теперь покажем, как определить угол между скрещивающимися прямыми. Пусть прямые m и n скрещиваются. Выберем в пространстве произвольную точку К. Через нее можно построить такие прямые m₁ и n₁, что m₁||m и n₁||n. Угол между m₁ и n₁ как раз и принимается за угол между скрещивающимися прямыми m и n:

Возникает вопрос – зависит ли величина измеренного таким образом угла от того, какая именно точка К выбрана? Оказывается, что не зависит, и это можно доказать. Выберем две произвольные точки К₁ и К₂. Через К₁ проведем прямые n₁ и m₁, а через К₂ проведем n₂ и m₂, которые будут соответственно параллельны исходным прямым m и n.

Так как n₁||n и n₂||n, то по свойству транзитивности параллельности и n₁||n₂. Аналогично и m₁||m₂. Получается, что стороны углов в точках К₁ и К₂ соответственно сонаправлены. Значит, они одинаковы, ч. т. д.

Задачи на скрещивающиеся прямые

Теоретический материал закончился, осталось научиться применять полученные знания. Перед просмотром решения постарайтесь самостоятельно решить каждую задачу.

Задание. Точка D находится вне плос-ти ∆АВС. Середины отрезков АD, BD и СD обозначены буквами M, N и P соответственно. Точка K располагается на отрезке BN (и не совпадает с концами этого отрезка). Определите, как относительно друг друга располагаются прямые:

Решение. Сначала важно построить правильный рисунок по описанию задачи:

Теперь можно рассмотреть по отдельности каждый пункт.

а) АВ и DN. Прямая DN совпадает с прямой BD. Она в свою очередь пересекается с АВ в точке В. Значит, в данном случае прямые пересекаются.

б) РК и ВС. Рассмотрим плос-ть треугольника ∆ВСD. Рассматриваемые прямые как раз находятся в ней. То есть они уже точно не скрещиваются. Могут ли они быть параллельны? Обратите внимание на отрезок NP. Это средняя линия в ∆ВСD, поэтому NP||ВС. Через Р может быть проведена лишь одна прямая, параллельная ВС (по аксиоме параллельности), и это NP. Значит, KP пересекает ВС.

в) MN и АВ. В ∆АВDMN является средней линией, поэтому MN||АВ.

г) МР и АС. МР – это средняя линия в ∆АСD, значит, МР||АС.

д) KN и АС. Прямая KN совпадает с прямой BD. Она пересекает плос-ть АСВ, но точка пересечения (это В) не находится на АС. Тогда по признаку скрещивающихся прямых можно утверждать, что KN и АС скрещиваются.

е) MD и ВС. MD пересекается с плос-тью АСВ в точке А. Тогда из признака скрещивающихся прямых вытекает, что MD и DC скрещиваются.

Задание. Через точку Р, не находящуюся на прямой m, проведены две различные прямые, не пересекающиеся с m. Верно ли, что хотя бы одна из них точно скрещивается с m?

Решение. Каждая из этих двух прямых с m не пересекается. Тогда они либо параллельны m, либо скрещиваются с ней. Но обе прямые параллельны m не могут быть параллельны m, ведь тогда через Р будет проведено сразу две прямые, параллельные m, что невозможно. Значит, хотя бы одна из прямых действительно скрещивается с m.

Задание. MК и РН – скрещивающиеся прямые.Скрещиваются ли прямые МН и КР?

Решение. Ясно, что точки М, К, Р, Н располагаются в различных плос-тях. В противном случае, если бы существовала плос-ть α, в которой находились бы М, К, Р и Н, то в α также находились бы прямые МК и РН, и тогда они уже по определению не были бы скрещивающимися.

Теперь рассмотрим плос-ть КРН. В ней находится прямая КР. А прямая МН ее пересекает в точке К. Тогда, по признаку скрещивающихся прямых, МН и КР скрещиваются.

Задание. Прямые m и n скрещиваются. M – точка на m, N – точка на n. Через m и N проведена плос-ть α, а через n и M – плос-ть β. Пересекаются ли плос-ти α и β, и если да, то по какой линии?

Посмотрим, есть ли у α и β общие точки. Плос-ть α проходит через n, то есть и через точку N тоже. Плос-ть β также проходит через N. Значит, N – общая точка. Аналогично можно показать, что и М – это общая точка. В итоге α и β пересекаются, причем на линии пересечения находятся точки M и N. Значит, именно прямая МN является границей этих двух плос-тей.

Задание. Известно, что MНКЕ – параллелограмм, а МНРТ – трапеция (РТ – её основание), причем они располагаются в разных областях. Каково расположение отрезков КЕ и РТ друг относительно друга.

Решение. Задачу можно решить и без рисунка. Если РТ – основание трапеции, то второе основание – это МН, и МН||РТ. В параллелограмме МНКЕ параллельны стороны МН и КЕ, ведь они противоположные. Тогда по свойству транзитивности параллельности из того факта, что МН||РТ и МН||КЕ, вытекает, что и РТ||КЕ.

Задание. Известно, что ОА и СD – скрещивающиеся прямые, а ОВ||CD. Чему равен угол между ОА и CD, если

Если CD||ОВ, то угол между CD и ОА совпадает с углом между ОВ и ОА. В задании а) он совпадет с ∠АОВ и составляет 40°. В случае б) угол не может составлять 135°, так как он не должен превышать 90°. Поэтому он равен

Наконец, в случае в) он составит 90°.

Ответ: а) 40°; б) 45°; в) 90°.

Задание. Дан куб, вершины которого обозначены так, как это показано на рисунке:

Найдите угол между прямыми:

Решение. Во всех трех случаях нам даны скрещивающиеся прямые. Для вычисления угла надо найти такие параллельные им прямые, которые будут пересекаться.

а) AD и GH. Заметим, что GH||СD, ведь это противоположные стороны квадрата СDHG, поэтому мы можем определить угол между AD и CD. Другими словами, мы просто заменяем в задаче GH на CD, так как эти отрезки параллельны. Так как отрезки AD и CD в свою очередь являются уже смежными сторонами в квадрате АВСD, то ∠ADC, который нам надо найти, составляет 90°.

б) BD и FG. Здесь уже уместно заменить FG на ВС. Это можно сделать, ведь FG||ВС (это стороны квадрата). Тогда нам необходимо вычислить ∠СВD. Он составляет 45°, ведь диагональ квадрата делит его угол пополам.

в) BD и AF. Здесь есть смысл AF заменить на GD. Но для этого надо сначала показать, что AF||DG.Рассмотрим отрезки AD и FG. Каждый из них параллелен ВС (по свойству квадратов ABCD и ВСGH). Значит, по свойству транзитивности AD||FG, то есть эти отрезки располагаются в одной плос-ти. Тогда AFGD – плоский четырехугольник.

Заметим, что отрезки AD и FG ещё и одинаковы, так каждый из них равен ВС (вообще в кубе все ребра одинаковы). Получается, что в четырехугольнике AFGD стороны AD и FG одинаковы и параллельны, а потому AFGD – параллелограмм, по одному из его признаков. Отсюда и вытекает, что AF||DG.

Мы поняли, искомый нами угол между прямыми равен∠BDG. Как его вычислить? Для этого надо рассмотреть ∆BDG. Можно заметить, что он равносторонний. Действительно, отрезки BG, GD и BD – это диагонали в равных квадратах ВСGH, СDHG, АВСD, поэтому и сами эти диагонали также одинаковы. В любом равностороннем треугольнике все углы составляют по 60°, поэтому и ∠BDG равен этому же значению, то есть 60°.

Ответ: а) 90°; б) 45°; в) 60°.

Задание (стереометрическая задача из ЕГЭ). Точки А, В, С и D в пространстве располагаются так, что расстояния между любыми двумя из этих точек одинаковы. Можно доказать (попробуйте сделать это самостоятельно), что такая ситуация возможна лишь в случае, когда точки не располагаются в одной плос-ти. М – середина ВС, а L – середина АВ. Найдите косинус угла между прямыми МD и CL.

Решение. Из условия вытекает, что ∆АВС, ∆ВСD, ∆ABD – равносторонние и притом равные друг другу. Проведем в ∆АВС отрезок такой отрезок MF, что MF||СL. Тогда нам необходимо вычислить ∠DMF (точнее, его косинус). Это можно сделать, используя теорему косинусов применительно к ∆MDF, но для этого сперва надо найти все стороны в этом треугольнике:

Для удобства обозначим длину отрезков АВ, ВС, АС, BD, AD и CD буквой R. Так как L– середина АВ, то CL– медиана в ∆АВС. Но в равностороннем треугольнике она одновременно будет и высотой. Тогда ∆АСL – прямоугольный. Запишем для него теорему Пифагора:

Аналогичным образом легко определить, что длина медианы DМ в ∆ВСD равна этому же значению:

Теперь исследуем ∆ВСL. Так как MF||CL и М – середина ВС, то MF оказывается средней линией в ∆ВСL. Значит, ее длина вдвое меньше, чем у СL:

Также из того факта, что МF – средняя линия, вытекает то, что F – середина LВ. Тогда можно вычислить FB:

Далее обратим внимание на ∆ВFD. ∠В в нем составляет 60°, ведь это одновременно и угол в равностороннем ∆АВD. Стороны FB и BD нам известны, а потому с помощью теоремы косинусов можно вычислить и FD:

Теперь можно составить и для ∆МDF уравнение на основе теореме косинуса, из которого удастся выяснить интересующий нас косинус ∠DMF:

В ходе сегодняшнего урока мы познакомились с новым понятием – скрещивающимися прямыми. Также мы узнали, как вычислять угол между ними. Подобные задачи могут встречаться и на ЕГЭ.

Источник