Что такое порядковая шкала

ШКАЛА, ПОРЯДКОВАЯ

Полезное

Смотреть что такое «ШКАЛА, ПОРЯДКОВАЯ» в других словарях:

ШКАЛА ПОРЯДКОВАЯ — англ. scale, ordinal; нем. Ordnungssfcala. Шкала, позволяющая устанавливать соотношение равенства, неравенства и последовательности между пунктами, при отсутствия точки отсчета и дистанции между ними. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии

ШКАЛА, ПОРЯДКОВАЯ — шкала, которая позволяет не только различать объекты, но и ранжировать их по степени проявления некоторого свойства, то есть измерят качественные признаки … Большой экономический словарь

шкала порядковая в социолингвистике — Шкала, дающая числовую оценку, указывающую на иерархию данных, порядок их следования … Словарь лингвистических терминов Т.В. Жеребило

Шкала порядковая в социолингвистике — Шкала, дающая числовую оценку, указывающую на иерархию данных, порядок их следования … Общее языкознание. Социолингвистика: Словарь-справочник

ШКАЛА ПОРЯДКОВАЯ (ОРДИНАЛЬНАЯ) — англ. scale, ordinal; нем. Ordnungssfcala. Шкала, позволяющая устанавливать соотношение равенства, неравенства и последовательности между пунктами, при отсутствия точки отсчета и дистанции между ними … Толковый словарь по социологии

ПОРЯДКОВАЯ ШКАЛА — См. шкала, порядковая … Толковый словарь по психологии

Порядковая Шкала — метрическая шкала, отображающая наряду с отношением эквивалентности еще и отношение порядка. Каждый элемент по выраженности шкалируемого признака сопоставляется с другими, но без использования единицы измерения; для такой шкалы возможно любое… … Психологический словарь

ШКАЛА СОЦИАЛЬНОЙ ДИСТАНЦИИ — (англ. Social Distance Scale) порядковая шкала, с помощью которой можно оценить уровень выраженности социальной установки в отношении представителей различных рас и национальностей. Фактически, аттитюд оценивается на основе уровня толерантности,… … Большая психологическая энциклопедия

Шкала личных предпочтений — [individual preference scale] (в моделях маркетинга) порядковая шкала, отражающая последовательность покупок различных марок товара в зависимости от предпочтений покупателя. Обычно включает четыре типа предпочтений: безраздельное предпочтение,… … Экономико-математический словарь

шкала — По ГОСТ 16263 70 [ГОСТ 21830 76] шкала Система чисел или иных элементов, принятых для оценки или измерения каких либо величин. Ш. в кибернетике и общей теории систем используются для оценки и выявления связей и отношений между элементами систем.… … Справочник технического переводчика

Источник

Управленческая теория измерений.

Шкалы и накладываемые ими ограничения

Управленческая теория измерений.

Шкалы и накладываемые ими ограничения

К. э. н., доцент кафедры финансового менеджмента, управленческого учёта и международных стандартов финансовой деятельности факультета ВШФМ РАНХиГС при Президенте РФ, руководитель консультационного бюро Института экономических стратегий, преподаватель школ бизнеса РАНХиГС, НИУ ВШЭ, МГУ, РСПП, ИНЭС и др.

Шкалы и их классификации

Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.

Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).

Шкалирование — это:

Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.

Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается.
Шкалы, как правило, объединяют в три основные группы:

Иногда все шкалы измерения делят на два класса:

Далее мы последовательно разберём все типы шкал.

Как считать очки в десятиборье?

Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.

Номинальные шкалы

Допустимые преобразования

Этим понятием математики строго описывают шкалы. Тип шкалы задаётся группой её допустимых преобразований.
Допустимые преобразования — это такие преобразования, которые не меняют соотношения между объектами измерения и, соответственно, выводы, сделанные по результатам измерений. Например, при измерении длины переход от аршинов к метрам не меняет соотношений между длинами рассматриваемых объектов: если первый объект длиннее второго в пять раз, то это будет установлено при измерении как в аршинах, так и в метрах. Обратите внимание, что при этом численное значение длины в аршинах отличается от длины в метрах — не меняется лишь результат сравнения длин двух объектов.
Аналогично денежные суммы можно сопоставлять как в рублях, так и в иностранной валюте. Особенность, связанная с изменяющимися курсами валют: результат сопоставления денежных сумм в разных валютах меняется во времени. С аршинами и метрами ситуация иная: их соотношение вечно. Вот вам и проблема курсовых разниц в экономике. О ней сейчас не место говорить, но запомните её.

Порядковые шкалы

Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними.
Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов.
Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен.
Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы.
Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:

Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.

Ранговые порядковые шкалы

Ранговые шкалы — это шкалы, где числа служат только для присвоения мест. Экспертов часто просят ранжировать (упорядочить) объекты экспертизы, то есть расположить их в порядке возрастания (или убывания) интенсивности исследуемой характеристики. Ранг — это номер объекта экспертизы в упорядоченном ряду значений характеристики у различных объектов. Формально ранги выражаются числами 1, 2, 3. Важно помнить, что измерения 1, 2, 3 и 6, 10, 50 означают одно и то же: первая альтернатива заняла первое место, вторая — второе место и т. д. В ранговых шкалах нет информации о величине различий между оцениваемыми объектами. Такие шкалы используются тогда, когда объект трудно описать несколькими характеристиками, которые потом оцениваются качественно (баллами, например) или количественно. В практике менеджмента рейтинги часто основаны на ранговых шкалах.

Ранговые измерения (процедуры ранжирования). Различают несколько основных типов алгоритмов ранжирования:

Простейший (и неверный) перевод результатов парных сравнений в ранги и в весовые коэффициенты

Заманчива идея получить весовые коэффициенты, то есть количественную меру, из порядковых измерений. Однако, как правило, такое действие некорректно — оно многозначно и потому единственный и корректный вывод для задач менеджмента невозможен. Вместе с тем оно популярно, особенно среди людей, плохо знающих математику.
Приведём пример наиболее простой и популярной модификации метода парных сравнений. Допустим, эксперт проводит оценку четырёх методов, которые связаны с решением кадровых вопросов в корпоративном проекте:
Z₁ — повышение квалификации в процессе выполнения проекта;
Z₂ — привлечение кадров со стороны;
Z₃ — подготовка кадров в своём корпоративном университете;
Z₄ — разовое повышение квалификации.

Zi/Zj	Z1	Z2	Z3	Z4
Z1	1	1	1
Z2	0	0	0
Z3	0	1	1
Z4	0	1	0

Составим матрицу бинарных предпочтений эксперта, где 1 означает, что один метод „предпочтительнее”, чем другой, с которым он сравнивается. Определим оценку каждого метода (складываем по строкам): C₁ = 3; C₂ = 0; C₃ = 2; C₄ = 1. Получаем порядок предпочтения методов: Z₁, Z₃, Z₄, Z₂. Пока всё это корректные действия. Затем наступает черед „творчества”.
Простейший (и неверный) перевод результатов парных сравнений в весовые коэффициенты. Если нужны „веса” указанных четырёх альтернатив, то можно нормировать числа <С>и получить „веса” делением каждого значения С на сумму всех С_i, равную шести: v₁ = 3/6 = 0,5; v₂ = 0; v₃ = 0,33; v₄ = 0,17. Проверка: сумма весов должна быть равна 1.
Однако анализ корректности метода даёт отрицательный результат. Дело в том, что объектам могут быть присвоены и другие веса (см. подобный пример ниже). Почему некорректно? Потому что в результате его применений вес v₁ оказывается в три раза больше, чем v₄, а этого эксперт, который проводил парное сравнение, не утверждал! Подделка очевидна, так как в результате обработки мы добавили весомую толику информации от себя к тому, что говорили эксперты.

Корректный перевод результатов парных сравнений в интервальную шкалу

При опросе экспертов в августе 2001 г. попарно сравнивалось качество бензина в четырех компаниях: «ТНК», «Лукойл», «Юкос» и «Татнефть». При сравнениях четырёх компаний получается 6 пар для сравнения:

Таблица 1. Сравнение компаний по качеству бензина

Пары	Частота выбора первого элемента пары	Частота выбора второго элемента пары
«ТНК» — «Лукойл»	π(1,2) = 0,508	π(2,1) = 0,492
«ТНК» — «Юкос»	π(1,3) = 0,331	π(3,1) = 0,669
«ТНК» — «Татнефть»	π(1,4) = 0,990	π(4,1) = 0,010
«Лукойл» — «Юкос»	π(2,3) = 0,338	π(3,2) = 0,662
«Лукойл» — «Татнефть»	π(2,4) = 0,990	π(4,2) = 0,010
«Юкос» — «Татнефть»	π(3,4) = 0,997	π(4,3) = 0,003

Балльные порядковые шкалы

Балльные шкалы используются очень часто, примеры мы уже приводили. Однако важно понимать, что каждому баллу необходимо присвоить качественную характеристику, в противном случае может пострадать корректность. Приведу пример: в конце 1990-х гг. я был назначен ответственным преподавателем (качество, контроль, апелляции) на устном экзамене по экономике для абитуриентов НИУ ВШЭ. Только что на ректорате ввели 10-балльную шкалу. Экспромт не удался — первый блин, как обычно, вышел комом. Моя работа заключалась, в том числе, и в „обеспечении справедливости”, то есть чтобы за примерно одни и те же ответы преподаватели в разных комиссиях ставили одинаковые баллы. Разброс в оценках оказался ужасающим — от 4 до 7 за похожие ответы. Буквально на следующий день ошибка в дефиниции шкалы была исправлена, а получившаяся шкала (см. таблица 2) успешно работает до сих пор (с небольшим изменением). Многие вузы взяли её на вооружение. Обращаю внимание читателей, что в соответствии со спецификой каждого предмета преподаватель конкретизирует шкалу.

Таблица 2. Пример 10-балльной шкалы для оценки успеваемости студентов.

Балл	Качественная характеристика
10	Пять с плюсом — исключительные знания (кое-что из ответа студента даже преподаватель не знал)
9	Отлично, твёрдая пятёрка
8	Пять с минусом
7	Четыре с плюсом
6	Четыре, твёрдая четвёрка
5	Четыре с минусом
4	Три с плюсом
3	Три, твёрдая оценка «удовлетворительно»
2	Три с минусом
1	Неудовлетворительно

Важный вопрос: какова идеальная размерность балльной шкалы? Ответ: сколько качеств, столько и баллов. Баллы обозначают упорядоченные качества, и каждому качеству присваивают свой балл. Обратное неверно: если взять за основу 10-балльную шкалу и каждому баллу попытаться „присвоить” определённое качество, то можно столкнуться с ситуацией, что качеств может оказаться не 10, а всего 7. Поэтому следует отталкиваться именно от количества качеств, которые вы можете выделить.

Балльные измерения. Балльные измерения формально просты, но коварны возможностью допустить необоснованные оценки и тем самым всё испортить. Существует два подхода к выставлению балльных оценок:

Перевод результатов балльных оценок в весовые коэффициенты. Если такой перевод делается одним экспертом — это операция сомнительная, но популярная. Во врезке приведён один из популярных методов — метод последовательных сравнений.

Перевод рангов в весовые коэффициенты одним экспертом. Метод последовательных сравнений

Количественные шкалы

Количественные шкалы отражают более высокий уровень измерений, учитывающий не только то, в каком отношении измеряемый объект находится с другими объектами, но и степень их различия. Примеры использования количественных шкал мы видим повсюду.
Допустимые преобразования. Количественные шкалы определены с точностью до преобразований, которые не меняют единицы измерения (линейных или иных функциональных преобразований).
Типы количественных шкал. Различают количественные шкалы:

Расположение шкал в этом списке не случайно. Первая (шкала интервалов) — самая слабая по информативности и самая сильная в плане надёжности оценок, последняя (абсолютная шкала) — наиболее информативная (измерения могут быть очень надёжными), но при этом допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу максимально затруднена — помните разницу между оценкой и измерением?
Шкала интервалов (интервальная шкала) точно определяет величину интервала между точками на шкале. Для проведения измерений необходимо задать интервал (2 точки). Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования вида: F(Х) = а · Х + b, где а > 0.

Шкала степенная. Шкала степеней (степенная) допускает степенное преобразование (F(Х) = АХВ). В области техники она вполне адекватна — у неё тоже две степени свободы, как у шкалы интервалов. В экономике она, напротив, является исключением, поэтому подробно рассматривать её не будем.

Шкала отношений. Из количественных шкал в науке и практике наиболее распространены шкалы отношений. В них есть естественное начало отсчёта — ноль (то есть отсутствие величины), но нет естественной единицы измерения.
Примеры использования шкалы отношений:

Шкала отношений допускает преобразования, изменяющие только масштаб, то есть преобразования подобия: F(Х) = аХ, где а > 0 (линейные возрастающие преобразования без свободного члена).
Примеры преобразования шкалы отношений:

Базовая точка в шкале отношений одна — «единица». Эта условная «единица» может быть, например, 100 (проценты) или 1 (доли). Таким образом, измерения в долях и процентах эквивалентны, что очевидно и без всякой теории.
Однако выводы, которые делаются по результатам процентных измерений, могут быть ошибочными (см. врезку). Возникают сопутствующие вопросы:

Корректность процентных измерений. Рейтинг Путина vs стоимость свинины

Вывод: по темпам роста (в научной терминологии «прироста») свинина побеждает Путина: 44% vs 68%.
Корректны ли эти измерения? Решите сами и объясните (что гораздо сложнее). Точно сформулировать, насколько такие сравнения корректны, удается лишь 10% слушателей программ МВА. Это ещё один довод в пользу изучения шкал. Хотя бы на уровне знакомства.

Степени свободы шкал

Для проведения измерений в шкалах отношений и разностей мы должны задавать одну точку. В шкале отношений она „играет роль единицы”, то есть соответствует переводу базового эмпирического элемента в единицу действительной оси. Для шкалы разностей это „нулевая точка”, то есть нужно задать отношение таким образом, чтобы „точка отсчёта” эмпирической системы превращалась в числовой ноль.
В этой связи математики различают шкалы по степеням свободы:

Иерархия шкал измерений

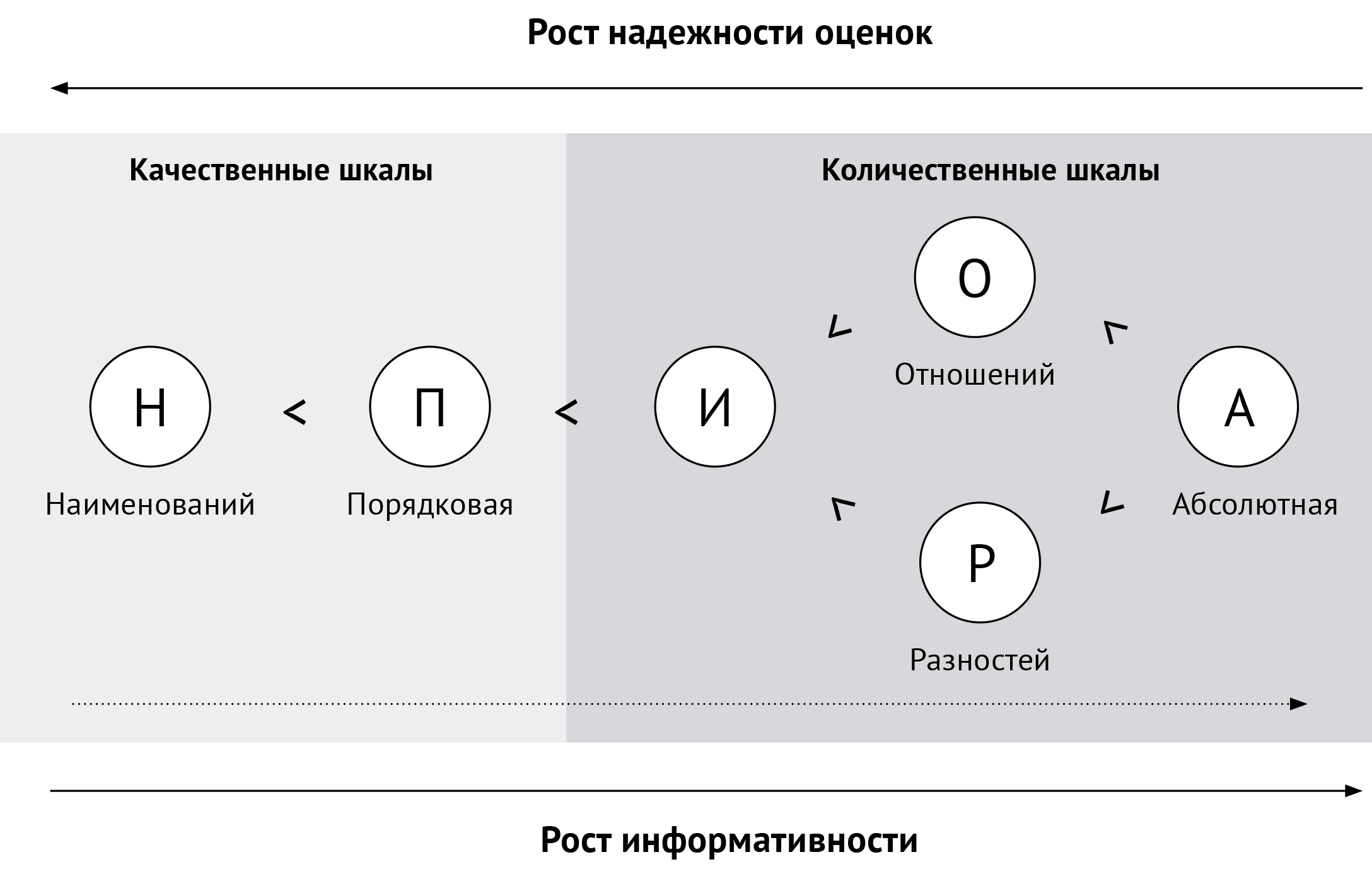
Напомним, что все шкалы делят на две большие группы: качественные и количественные. Наиболее распространённая классификация шкал — континуальная (рис. 3). В ней шкалы упорядочены по мере повышения их способности удовлетворять требованиям информативности и надёжности проведения оценок. Слева — самая слабая по информативности и самая надёжная, справа — наиболее информативная и наименее надёжная.

Рис. 3. Иерархия шкал измерений

В следующей части мы поговорим о том, как собственно выставлять оценки чему-либо. Хорошая обработка результатов измерений — это достоверная система оценок. А какими математическими свойствами она должна обладать? Есть ли научный ответ на этот вопрос?

Источник

Данные

Измерения

Многие инструменты Data Mining при импорте данных из других источников предлагают выбрать тип шкалы для каждой переменной и/или выбрать тип данных для входных и выходных переменных (символьные, числовые, дискретные и непрерывные). Пользователю такого инструмента необходимо владеть этими понятиями.

Переменные могут являться числовыми данными либо символьными.

Дискретные данные являются значениями признака, общее число которых конечно либо бесконечно, но может быть подсчитано при помощи натуральных чисел от одного до бесконечности.

Шкалы

Существует пять типов шкал измерений: номинальная, порядковая, интервальная, относительная и дихотомическая.

Номинальная шкала состоит из названий, категорий, имен для классификации и сортировки объектов или наблюдений по некоторому признаку.

Пример такой шкалы : профессии, город проживания, семейное положение.

Для этой шкалы применимы только такие операции: равно (=), не равно ( ).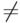

Шкала измерений дает возможность ранжировать значения переменных. Измерения же в порядковой шкале содержат информацию только о порядке следования величин, но не позволяют сказать «насколько одна величина больше другой», или «насколько она меньше другой».

Пример такой шкалы : место (1, 2, 3-е), которое команда получила на соревнованиях, номер студента в рейтинге успеваемости (1-й, 23-й, и т.д.), при этом неизвестно, насколько один студент успешней другого, известен лишь его номер в рейтинге.

Для этой шкалы применимы только такие операции: равно (=), не равно ( 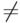), больше (>), меньше ( шкала позволяет находить разницу между двумя величинами, обладает свойствами номинальной и порядковой шкал, а также позволяет определить количественное изменение признака.

Для этой шкалы применимы только такие операции: равно (=), не равно ( 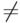), больше (>), меньше ( шкалы : вес новорожденного ребенка (4 кг и 3 кг). Первый в 1,33 раза тяжелее.

Цена на картофель в супермаркете выше в 1,2 раза, чем цена на базаре.

Относительные и интервальные шкалы являются числовыми.

Для этой шкалы применимы только такие операции: равно (=), не равно ( 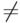), больше (>), меньше ( шкалы : пол (мужской и женский).

Таблица 2.2. Множество измерений свойств различных объектов

Номер объекта	Профессия (номинальная шкала)	Средний балл (интервальная шкала)	Образование (порядковая шкала)
1	слесарь	22	среднее
2	ученый	55	высшее
3	учитель	47	высшее

Таблица 2.3. Множество измерений свойств одной системы

Дата измерения	Облачность (номинальная шкала)	Температура в 8 часов утра (интервальная шкала)	Сила ветра (порядковая шкала)
1 сентября	облачно	22 С	Ветер сильный
2 сентября	пасмурно	17 С	Ветер слабый
3 сентября	ясно	23 С	Ветер очень сильный

Источник