Что такое порядок дифракции

Что такое дифракционная решетка: определение, длина и принцип действия

Одним из важных оптических приборов, нашедших свое применение при анализе спектров излучения и поглощения, является дифракционная решетка. В данной статье приведена информация, позволяющая понять, что такое дифракционная решетка, в чем заключается принцип ее работы и как самостоятельно можно рассчитать положение максимумов на дифракционной картине, которую она дает.

Дифракция и интерференция

В начале XIX столетия английский ученый Томас Юнг, изучая поведение монохроматического пучка света при его разделении пополам тонкой пластиной, получил дифракционную картину. Она представляла собой последовательность ярких и темных полос на экране. Используя представления о свете, как о волне, Юнг правильно объяснил результаты своих опытов. Картина, которую он наблюдал, возникала благодаря явлениям дифракции и интерференции.

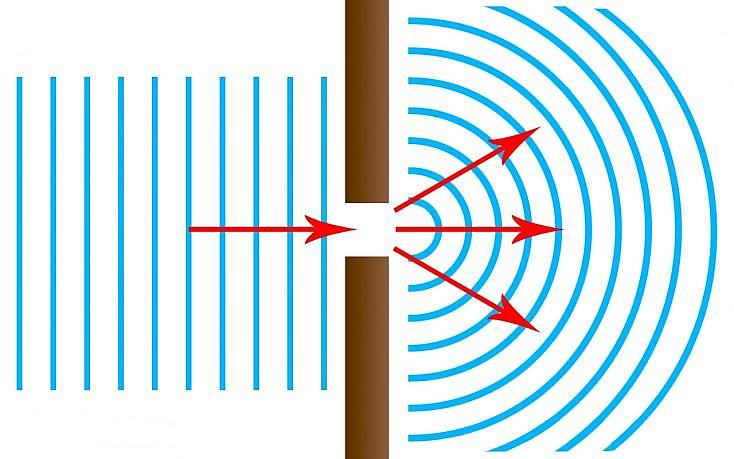
Под дифракцией понимают искривление прямолинейной траектории распространения волны, когда она попадает на непрозрачное препятствие. Дифракция может проявляться в результате огибания волной препятствия (такое возможно, если длина волны намного больше препятствия) либо в результате искривления траектории, когда размеры препятствия сравнимы с длиной волны. Примером для последнего случая является проникновение света в щели и небольшие круглые отверстия.

Вам будет интересно: Цвет и запах соли

Явление интерференции заключается в накладывании одних волн на другие. Результатом такого накладывания является искривление синусоидальной формы результирующей волны. Частными случаями интерференции являются либо максимальное усиления амплитуды, когда две волны приходят в рассматриваемую зону пространства в одной фазе, либо полное затухание волнового процесса, когда обе волны встречаются в данной зоне в противофазе.

Описанные явления позволяют понять, что такое дифракционная решетка и как она работает.

Дифракционная решетка

Уже само название говорит, что такое дифракционная решетка. Она представляет собой объект, который состоит из периодически чередующихся прозрачных и непрозрачных полос. Получить ее можно, если постепенно увеличивать число щелей, на которые падает волновой фронт. Это понятие в общем случае применимо для любой волны, однако использование оно нашло только для области видимого электромагнитного излучения, то есть для света.

Дифракционную решетку принято характеризовать тремя главными параметрами:

Прозрачные и отражающие решетки

Вам будет интересно: Период полураспада цезия-137. Биологические свойства цезия

Выше было описано, что такое дифракционная решетка. Теперь ответим на вопрос о том, что в действительности она собой представляет. Существуют два вида таких оптических объектов: прозрачные и отражающие.

Принцип работы решетки

Для примера рассмотрим прозрачный оптический прибор. Предположим, что на дифракционную решетку падает свет, имеющий плоский фронт. Это очень важный момент, поскольку приведенные ниже формулы учитывают, что волновой фронт является плоским и параллельным самой пластинке (дифракция Фраунгофера). Распределенные по периодическому закону штрихи вносят в этот фронт возмущение, в результате которого на выходе из пластинки создается ситуация, будто работают множество вторичных когерентных источников излучения (принцип Гюйгенса-Френеля). Эти источники приводят к появлению дифракции.

От каждого источника (щели между штрихами) распространяется волна, которая является когерентной всем остальным N-1 волнам. Теперь предположим, что на некотором расстоянии от пластинки помещается экран (расстояние должно быть достаточным, чтобы число Френеля было намного меньше единицы). Если смотреть на экран вдоль перпендикуляра, проведенного к центру пластинки, то в результате интерференционного наложения волн от этих N источников для некоторых углов θ будут наблюдаться яркие полосы, между которыми будет тень.

Поскольку условие интерференционных максимумов является функцией длины волны, то если падающий на пластинку свет был белым, на экране будут появляться разноцветные яркие полосы.

Основная формула

Как было сказано, падающий плоский фронт волны на дифракционную решетку отображается на экране в виде ярких полос, разделенных областью тени. Каждая яркая полоса называется максимумом. Если рассмотреть условие усиления волн, приходящих в рассматриваемую область в одинаковой фазе, то можно получить формулу максимумов дифракционной решетки. Она имеет следующий вид:

Зная период решетки d и длину волны λ, которая падает на нее, можно рассчитать положение всех максимумов. Отметим, что вычисленные по формуле выше максимумы называются главными. В действительности между ними существует целый набор более слабых максимумов, которые часто в эксперименте не наблюдаются.

Не стоит думать, что от ширины каждой щели на дифракционной пластинке картина на экране не зависит. Ширина щели не влияет на положение максимумов, однако она влияет на их интенсивность и ширину. Так, с уменьшением щели (с увеличением числа штрихов на пластинке) снижается интенсивность каждого максимума, а его ширина увеличивается.

Дифракционная решетка в спектроскопии

Разобравшись с вопросами о том, что такое дифракционная решетка и как находить максимумы, которые она дает на экране, любопытно проанализировать, что будет происходить с белым светом, если им облучить пластинку.

Выпишем снова формулу для главных максимумов:

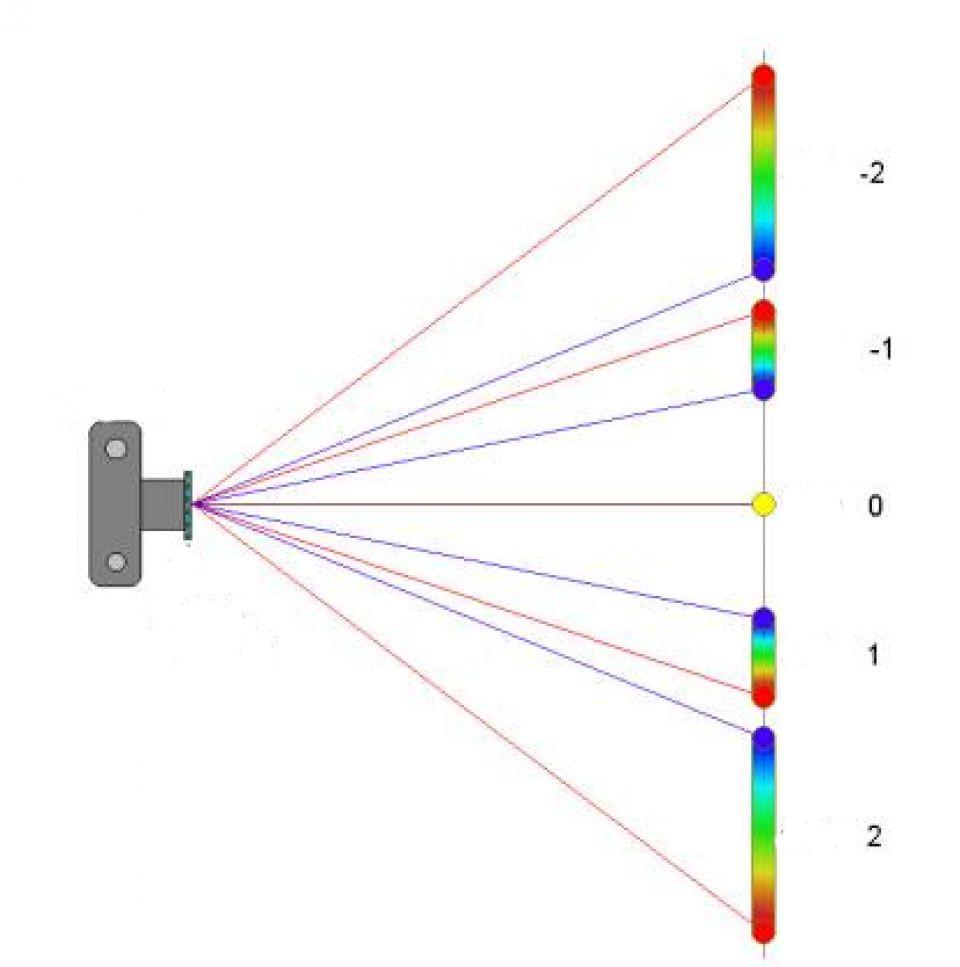
Если рассматривать конкретный порядок дифракции (например, m = 1), то видно, что чем больше λ, тем дальше от центрального максимума (m = 0) будет находиться соответствующая яркая линия. Это означает, что белый свет расщепляется на ряд цветов радуги, которые отображаются на экране. Причем, начиная от центра, сначала будут появляться фиолетовый и синий цвета, а затем будут идти желтый, зеленый и самый дальний максимум первого порядка будет соответствовать красному цвету.

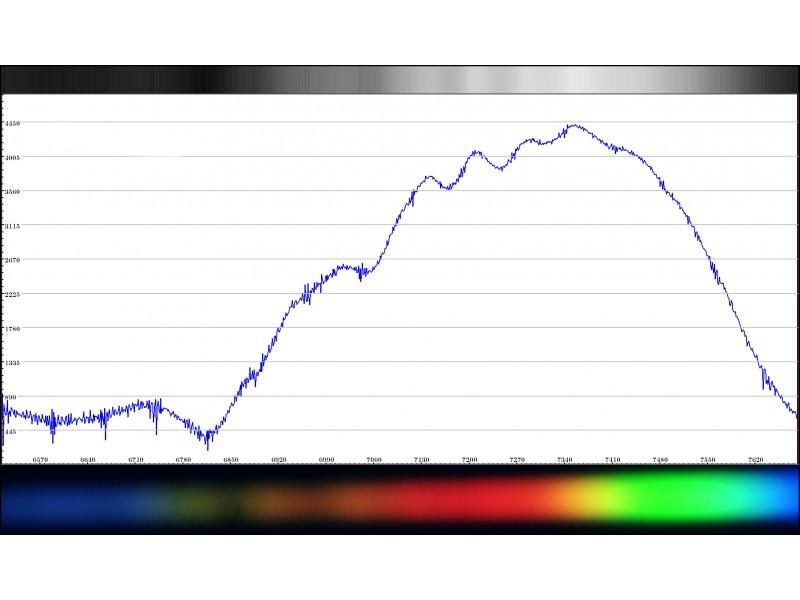
Свойство дифракционной решетки длины волн используется в спектроскопии. Когда необходимо узнать химический состав светящегося объекта, например, далекой звезды, то ее свет собирают зеркалами и направляют на пластинку. Измеряя углы θm, можно определить все длины волн спектра, а значит, и химические элементы, которые их излучают.

Ниже приводится видео, которое демонстрирует способность решеток с разным числом N расщеплять свет от лампы.

Понятие «угловая дисперсия»

Под этой величиной понимают изменения угла возникновения максимума на экране. Если изменить на небольшую величину длину монохроматического света, то получим:

Если левую и правую части равенства в формуле для главных максимумов продифференцировать по θm и λ соответственно, то можно получить выражение для дисперсии. Оно будет равно:

Дисперсию необходимо знать при определении разрешающей способности пластинки.

Что такое разрешающая способность?

Говоря простыми словами, это способность дифракционной решетки разделять две волны с близкими значениями λ на два отдельных максимума на экране. Согласно критерию лорда Рэлея, две линии можно различить, если угловая дистанция между ними окажется больше половины их угловой ширины. Полуширина линии определяется по формуле:

Различие между линиями в соответствии с критерием Рэлея возможно, если:

Подставляя формулу для дисперсии и полуширины, получаем конечное условие:

Разрешающая способность решетки повышается с увеличением числа щелей (штрихов) на ней и с ростом порядка дифракции.

Решение задачи

Применим полученные знания для решения простой задачи. Пусть на дифракционную решетку падает свет. Известно, что длина волны равна 450 нм, а период решетки составляет 3 мкм. Какой максимальный порядок дифракции можно наблюдать на кране?

Для ответа на вопрос следует подставить данные в уравнение решетки. Получаем:

Так как синус больше единицы быть не может, тогда получаем, что максимальный порядок дифракции для указанных условий задачи равен 6.

Источник

Дифракция света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: дифракция света, дифракционная решётка.

Пусть, например, плоская волна падает на экран с достаточно узкой щелью (рис. 1 ). На выходе из щели возникает расходящаяся волна, и эта расходимость усиливается с уменьшением ширины щели.

Рис. 1. Дифракция на щели

Вообще, дифракционные явления выражены тем отчётливей, чем мельче препятствие. Наиболее существенна дифракция в тех случаях, когда размер препятствия меньше или порядка длины волны. Именно такому условию должна удовлетворять ширина щели на рис. 1.

Так, на рис. 2 изображена дифракционная картина, полученная в результате прохождения лазерного луча сквозь небольшое отверстие диаметром 0,2мм.

Рис. 2. Дифракция лазерного луча на отверстии

Напоминает интерференцию, не правда ли? Это она и есть; данные кольца являются интерференционными максимумами и минимумами. Какие же волны тут интерферируют? Скоро мы разберёмся с этим вопросом, а заодно и выясним, почему вообще наблюдается дифракция.

Опыт Юнга.

Всякий эксперимент с интерференцией света содержит некоторый способ получения двух когерентных световых волн. В опыте с зеркалами Френеля, как вы помните, когерентными источниками являлись два изображения одного и того же источника, полученные в обоих зеркалах.

Но если Солнце является чрезмерно «большим», то нужно искусственно создать точечный первичный источник. С этой целью в опыте Юнга использовано маленькое предварительное отверстие (рис. 3 ).

Рис. 3. Схема опыта Юнга

Томас Юнг осуществил этот эксперимент, измерил ширину интерференционных полос, вывел формулу и с помощью этой формулы впервые вычислил длины волн видимого света. Вот почему этот опыт вошёл в число самых знаменитых в истории физики.

Принцип Гюйгенса–Френеля.

Напомним формулировку принципа Гюйгенса: каждая точка, вовлечённая в волновой процесс, является источником вторичных сферических волн; эти волны распространяются от данной точки, как из центра, во все стороны и накладываются друг на друга.

Но возникает естественный вопрос: а что значит «накладываются»?

В таком виде принцип Гюйгенса не давал ответа на вопрос, почему в процессе распространения волны не возникает волна, идущая в обратном направлении. Не объяснёнными оставались и дифракционные явления.

Модификация принципа Гюйгенса состоялась лишь спустя 137 лет. Огюстен Френель заменил вспомогательные геометрические сферы Гюйгенса на реальные волны и предположил, что эти волны интерферируют друг с другом.

Принцип Гюйгенса–Френеля. Каждая точка волновой поверхности служит источником вторичных сферических волн. Все эти вторичные волны являются когерентными ввиду общности их происхождения от первичного источника (и, стало быть, могут интерферировать друг с другом); волновой процесс в окружающем пространстве есть результат интерференции вторичных волн.

Идея Френеля наполнила принцип Гюйгенса физическим смыслом. Вторичные волны, интерферируя, усиливают друг друга на огибающей своих волновых поверхностей в направлении «вперёд», обеспечивая дальнейшее распространение волны. А в направлении «назад» происходит их интерференция с исходной волной, наблюдается взаимное гашение, и обратная волна не возникает.

В частности, свет распространяется там, где вторичные волны взаимно усиливаются. А в местах ослабления вторичных волн мы будем видеть тёмные участки пространства.

Принцип Гюйгенса–Френеля выражает важную физическую идею: волна, удалившись от своего источника, в дальнейшем «живёт своей жизнью» и уже никак от этого источника не зависит. Захватывая новые участки пространства, волна распространяется всё дальше и дальше вследствие интерференции вторичных волн, возбуждённых в различных точках пространства по мере прохождения волны.

Как принцип Гюйгенса–Френеля объясняет явление дифракции? Почему, например, происходит дифракция на отверстии? Дело в том, что из бесконечной плоской волновой поверхности падающей волны экранное отверстие вырезает лишь маленький светящийся диск, и последующее световое поле получается в результате интерференции волн вторичных источников, расположенных уже не на всей плоскости, а лишь на этом диске. Естественно, новые волновые поверхности теперь не будут плоскими; ход лучей искривляется, и волна начинает распространяться в разных направлениях, не совпадающих с первоначальным. Волна огибает края отверстия и проникает в область геометрической тени.

Дифракционная решётка.

Рис. 4. Дифракционная решётка

Дифракционная решётка изготавливается с помощью так называемой делительной машины, которая наносит штрихи на поверхность стекла или прозрачной плёнки. При этом штрихи оказываются непрозрачными промежутками, а нетронутые места служат щелями. Если, например, дифракционная решётка содержит 100 штрихов на миллиметр, то период такой решётки будет равен: d= 0,01 мм= 10 мкм.

Сперва мы посмотрим, как проходит сквозь решётку монохроматический свет, т. е. свет со строго определённой длиной волны. Отличным примером монохроматического света служит луч лазерной указки длина волны около 0,65 мкм).

На рис. 5 мы видим такой луч, падающий на одну из дифракционных решёток стандартного набора. Щели решётки расположены вертикально, и на экране за решёткой наблюдаются периодически расположенные вертикальные полосы.

Рис. 5. Дифракция лазерного луча на решётке

Теория дифракционной решётки весьма сложна и во всей своей полноте оказывается далеко за рамками школьной программы. Вам следует знать лишь самые элементарные вещи, связанные с одной-единственной формулой; эта формула описывает положения максимумов освещённости экрана за дифракционной решёткой.

Рис. 6. Дифракция на решётке

Интерференционные максимумы наблюдаются в тех случаях, когда разность хода равна целому числу длин волн:

Формула (1) позволяет найти углы, задающие направления на максимумы:

Этот угол задаёт направления на максимумы первого порядка. Их два, и расположены они симметрично относительно центрального максимума. Яркость в максимумах первого порядка несколько меньше, чем в центральном максимуме.

Аналогично, при имеем угол:

Он задаёт направления на максимумы второго порядка. Их тоже два, и они также расположены симметрично относительно центрального максимума. Яркость в максимумах второго порядка несколько меньше, чем в максимумах первого порядка.

Рис. 7. Максимумы первых двух порядков

Вообще, два симметричных максимума k-го порядка определяются углом:

С помощью дифракционной решётки можно измерить неизвестную длину волны. Направляем пучок света на решётку (период которой мы знаем), измеряем угол на максимум первого
порядка, пользуемся формулой (1) и получаем:

Дифракционная решётка как спектральный прибор.

Предположим, что на дифракционную решётку падает белый свет. Давайте вернёмся к формуле (2) и подумаем, какие выводы из неё можно сделать.

Положение центрального максимума ( ) не зависит от длины волны. В центре дифракционной картины сойдутся с нулевой разностью хода все монохроматические составляющие белого света. Поэтому в центральном максимуме мы увидим яркую белую полосу.

Рис. 8. Дифракция белого света на решётке

Спектральное разложение белого света, даваемое дифракционной решёткой, проще всего наблюдать, глядя на обычный компакт-диск (рис. 9 ). Оказывается, дорожки на поверхности диска образуют отражательную дифракционную решётку!

Источник

Дифракция света

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Рис. 1. Дифракция на щели

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке.

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Рис. 2. Дифракционная решётка (лучи)

Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

Тогда положения максимумов и минимумов дифракции:

Рис. 3. Дифракционная решётка (максимумы)

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Источник

Дифракционные решетки

Дифракционные решетки

Дифракционные решетки, пропускающие и отражательные, предназначены для пространственного деления электромагнитной волны в спектр. Когерентные пучки интерферируют, претерпевая дифракцию на периодической структуре. В пропускающих дифракционных решетках периодическая структура является множеством плотно расположенных узких щелей. При решении задачи о распределении интенсивности и записи ответа в виде функции, зависящей от длины волны и координаты на множестве щелей, получается общее выражение, которое справедливо для всех дифракционных решеток при θ_i = 0°:

(1)

Это выражение также называют уравнением дифракционной решетки. Оно означает, что дифракционная решетка с периодом a преломляет свет дискретно, прошедшие лучи составляют с нормалью угол дифракции θ_m в зависимости от значения mλ, m – номер главного максимума. При заданном порядке m различные длины волн излучения будут выходить из решетки под разными углами. Для белого света происходит разложение в непрерывный спектр, зависящий от угла.

Пропускающая решетка

Рисунок 1. Пропускающая решетка

Один из распространенных типов решеток – пропускающая решетка. Периодическая структура решеток создается путем вырезания или гравировки на прозрачной подложке параллельных штрихов. На такой поверхности свет может рассеиваться. Пример пропускающей решетки приведен на рис. 1.

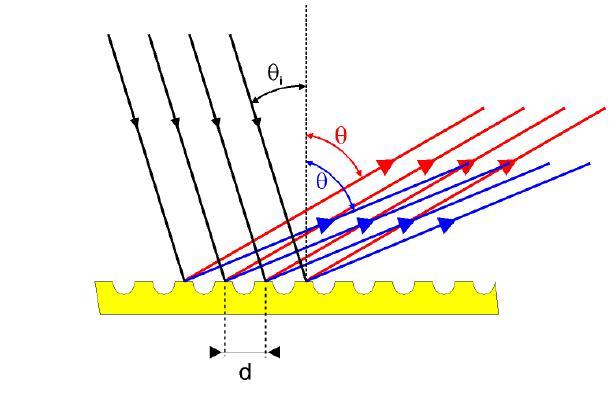
Пропускающая решетка, показанная на рис. 1, обладает периодической структурой благодаря узким штрихам с периодом a. Падающий свет попадает на решетку под углом θ_i, который отсчитывается от нормали к поверхности. Свет порядка m выходит из решетки под углом θ_m, который также определяется от нормали. Используя некоторые геометрические соотношения и общее выражение для дифракционной решетки (1), для пропускающей дифракционной решетки получим:

(2)

где углы θ_i и θ_m положительны, если падающий и дифрагированный свет оказываются на противоположных сторонах нормали к поверхности решетки, как показано на рис. 1. Если эти лучи находятся на той же стороне нормали решетки, то углы следует считать отрицательными.

Отражательная решетка

Рисунок 2. Отражательная решетка

Другой распространенный тип решеток – отражательная решетка. Отражательные решетки получают путем нанесения металлического покрытия на подложку и формирования параллельных штрихов на полученной поверхности. Также существует технология производства из эпоксидных и/или пластиковых оттисков от контрольного шаблона. Во всех случаях свет отражается от поверхности с нанесенными штрихами под разными углами, которые соответствуют разным порядкам и длинам волн. Пример отражательной решетки показан на рис. 2. Используя геометрическую схему, аналогичную приведенной выше, получается уравнение отражательной решетки:

(3)

где угол θ_i – положительный и угол θ_m – отрицательный, если падающий и дифрагированный свет оказываются на противоположных сторонах нормали к поверхности решетки, как показано на рис. 2. Если эти лучи находятся на одной стороне нормали решетки, то оба угла следует считать положительными.

Описанная проблема может быть решена с помощью особого рельефа, наносимого на поверхность вместе со штрихами. Дифракционные решетки такого типа называют рельефно-фазовыми. Их пример приведен на рис. 3.

Рельефно-фазовые (нарезные) решетки

Рисунок 3. Геометрия рельефно-фазовой решетки

Рисунок 4. Отражение нулевого порядка от рельефно-фазовой решетки

Рельефно-фазовые решетки (также известные как эшелетты) – особый вид отражательной или пропускающей дифракционной решетки, которые используют для достижения максимальной эффективности решетки в определенном порядке дифракции. Таким образом можно повысить мощность излучения при дифракции, минимизировав потери излучения других порядков (в частности нулевых). Благодаря своей конструкции, рельефно-фазовые решетки работают с определенной длиной волны, которую также называют длиной волны блеска.

Длина волны блеска – одна из основных характеристик рельефно-фазовых решеток. К таковым характеристикам также относятся другие два параметра, указанные на рис. 3: a – расстояние между гранями, γ – угол блеска (угол наклона грани штриха). Угол блеска может быть измерен от нормали к поверхности и от нормали к грани.

Геометрия концентрирующих решеток сходна с пропускающими и отражательными решетками. Углы падения θ_i и отражения θ_m максимумов порядка m отсчитываются от нормали к поверхности решетки. Существенное отличие заключается в том, что угол отражения зависит от угла блеска, но не от нормали поверхности решетки. Таким образом можно регулировать эффективность дифракции, изменяя только угол блеска дифракционной решетки.

Отражение нулевого порядка от рельефно-фазовой решетки показано на рис. 4. Падающий под углом θ_i луч отражается под углом θ_m при m = 0. Из уравнения (3) выводится единственное решение θ_i = – θ_m, что аналогично отражению от плоской поверхности.

Рисунок 5. Отражение света от грани рельефно-фазовой решетки

Рисунок 6. Нормальное падение света на рельефно-фазовую решетку

Отражение от рельефно-фазовой решетки отличается от отражения света в случае плоской поверхности за счет профиля штрихов, как видно из рис. 5. Зеркальное отражение от рельефно-фазовой решетки происходит из-за угла блеска. Этот угол считается отрицательным, если он находится на той же стороне нормали поверхности решетки, что и угол падения. Выполнив несколько простых геометрических преобразований, можно обнаружить следующее:

(4)

(5)

Схема Литтроу

Рельефно-фазовые решетки с конфигурацией Литтроу широко применяются в монохроматорах и спектрометрах из-за особенности периодической структуры. Пусть при падении света под углом θ_i эффективность решетки максимальна. По схеме Литтроу угол падения равен углу дифрагированных лучей, вышедших из решетки, θ_i = θ_m, тогда для ненулевых порядков дифракции получим:

(6)

Рисунок 7. Схема Литтроу

Угол Литтроу θ_L отсчитывается от точки наибольшей интенсивности (m = 1), λ_D – рабочая длина волны, a – постоянная решетки. Легко увидеть, что угол в схеме Литтроу равен углу блеска для рабочей длины волны. Соответствующие сведения даны в таблицах спектральных характеристик решеток.

(7)

Также можно вывести, что увеличение углового разделения длины волны сопровождается ростом порядка дифракции для света с нормальным падением, то есть при нулевом угле падения θ_m растет так же, как порядок m. Существует два основных недостатка дифракционной картины более высокого порядка по сравнению с дифракционной картиной низкого порядка: во-первых, уменьшение эффективности дифракции более высоких порядков, во-вторых, уменьшение свободного спектрального диапазона, определяемого соотношением:

(8)

где λ – центральная длина волны, m – порядок.

Первая проблема, возникающая при наблюдении дифракционных картин высоких порядков, решается с помощью использования эшелеттов. Этот тип решеток обладает наибольшим углом блеска и относительно низкой плотностью штрихов, благодаря чему удается достичь достаточной концентрации энергии излучения при дифракции излучения высоких порядков. Второй недостаток компенсируют, добавляя в систему специальную дополнительную оптику: решетку, рассеивающую призму или иную оптику, обладающую рассеивающими свойствами.

Голографические решетки

Рисунок 8. Голографическая решетка

Рельефно-фазовые решетки обладают наибольшей эффективностью при использовании на рабочей длине волны. Однако на их работу серьезно влияют периодические ошибки – дублирование, большая доля рассеянного света. Все это негативно сказывается на измерениях, требующих высокой точности. Потому во многих экспериментах применяют голографические решетки, эффективность которых ниже, однако стабильность выше.

Голографические решетки в промышленном масштабе производят тем же способом, что и нарезные: копированием контрольного образца. Шаблон голографической решетки изготавливают методом фотолитографии: действием на светочувствительный материал двух интерферирующих лазерных пучков. При этом интерференционная картина экспонируется на поверхность в виде периодической структуры. Пример голографической решетки приведен на рис. 8.

Замечание: дисперсия зависит от числа штрихов на мм, но не от формы самих штрихов. Следовательно, уравнение решетки для расчета углов можно применять и в случае голографических решеток.

Факторы, которые необходимо учитывать при выборе дифракционной решетки:

1. Эффективность

Нарезные решетки демонстрируют более высокую производительность в сравнении с голографическими решетками, однако последние имеют более широкий рабочий диапазон. Обычно нарезные решетки применяют в исследованиях флуоресценции и в опытах, связанных с переизлучением.

2. Длина волны блеска

Нарезные решетки имеют пилообразный профиль, который получается вследствие нанесения штрихов на подложку. В результате пик интенсивности таких решеток достигается при излучении, близком к длине волны блеска. Голографические решетки имеют синусоидальный профиль, потому пик интенсивности достигается на рабочей длине волны. Нарезные решетки в основном применяются в приложениях с узким волновым диапазоном.

3. Светорассеяние

Из-за различия в способах нанесения штрихов голографические и нарезные решетки имеют разницу в светорассеянии. Промышленное нанесение штрихов нарезным способом повышает вероятность ошибок, а фотолитографический способ изготовления решеток более стабилен, в связи с чем голографические решетки имеют меньшее светорассеяние. Их применяют в рамановской спектроскопии.

4. Разрешающая способность

Разрешающая способность решетки – расстояние, на котором возможно различить две длины волны. Оно определяется согласно критерию Рэлея применительно к дифракционному максимуму. Две длины волны различимы, когда максимум одной длины волны совпадает с минимумом второй. Хроматическая разрешающая способность определяется из соотношения R = λ/Δλ = nN, где Δλ – разрешаемая разница длин волн, n – порядок дифракции, N – число подсвеченных штрихов. Благодаря низкой плотности штрихов эшеллеты имеют высокое разрешение.

Правила работы с дифракционными решетками

Поверхность дифракционных решеток легко повреждается отпечатками пальцев, аэрозолями, после контакта с влагой. Малейший контакт с абразивными частицами также приводит к неисправностям. Необходимо соблюдать строгие требования по эксплуатации: например, переносить решетку можно только держа за боковые стороны. Необходимы латексные перчатки или любые другие меры защиты рабочей поверхности от отпечатков пальцев. Контакт с растворителями также следует исключить. Не предпринимайте иных попыток чистить решетку, кроме сдувания пыли чистым, сухим воздухом или азотом. Незначительные дефекты на поверхности решетки обычно не влияют на производительность.

Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Thorlabs на территории РФ

Источник