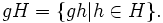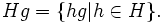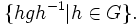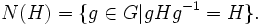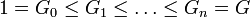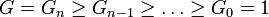Что такое порядок элемента
Порядок элемента
Для общего описания теории групп см. Группа (математика) и Теория групп.
Курсив обозначает ссылку на этот словарь.
p-группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о примарной группе. Более подробно см. в статье конечная p-группа.
Аддитивная группа кольца ― группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.
Антигомоморфизм групп — отображение групп f : (G,*) → (H,×) такое, что
для произвольных a и b в G (сравните с гомоморфизмом).
Гомоморфизм групп — отображение групп 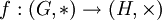
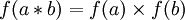
Группа Шмидта — это ненильпотентная группа, все собственные подгруппы которой нильпотентны.
Группа Миллера — Морено — это неабелева группа, все собственные подгруппы которой абелевы.
Групповая алгебра группы G над полем K — это векторное пространство над K, образующими которого являются элементы G, а умножение образующих соответсвует умножению элементов G.
Длина ряда подгрупп — число n в определении ряда подгрупп.
Изоморфизм групп — биективный гомоморфизм.
Изоморфные группы — группы, между которыми существует хотя бы один изоморфизм.
Индекс подгруппы H в группе G — число смежных классов в каждом (правом или левом) из разложений группы G по этой подгруппе H.
Индексы ряда подгрупп — индексы | Gi + 1:Gi | в определении субнормального ряда подгрупп.
Класс смежности/смежный класс (левый или правый) подгруппы H в G. Левый класс смежности элемента 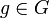
Аналогично определяется правый класс смежности:
Класс сопряжённости элемента 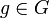
Коммутант группы есть подгруппа, порождённая всеми коммутаторами группы, обычно обозначается [G,G] или 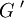
Коммутативная группа. Группа G является коммутативной, или абелевой, если её операция * коммутативна, то есть g*h=h*g 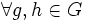
Коммутатор подгрупп — множество всевозможных произведений 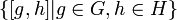
Композиционный ряд группы G — ряд подгрупп, в котором все факторы Gi + 1 / Gi — простые группы.
Конечная группа — группа с конечным числом элементов.
Конечно определённая группа — группа, обладающая конечным числом образующих и задаваемая в этих образующих конечным числом соотношений.
Конечнопорождённая группа — группа, обладающая конечной системой образующих.
Кручение, TorG, коммутативной или нильпотентной группы G есть подгруппа всех элементов конечного порядка.
Локальная теорема. Говорят, что для некоторого свойства P групп справедлива локальная теорема, если всякая группа, локально обладающая этим свойством, сама обладает им.
Например: локально абелева группа является абелевой, но локально конечная группа может быть бесконечной.
Метабелева группа ― группа, второй коммутант которой тривиален (разрешимая ступени 2).
Метациклическая группа ― группа, обладающая циклической нормальной подгруппой, факторгруппа по которой также циклическая. Всякая конечная группа, порядок которой свободен от квадратов (то есть не делится на квадрат какого-либо числа), является метациклической.
Мультипликативная группа тела ― группа, элементами которой являются все ненулевые элементы данного тела, а операция совпадает с операцией умножения в теле.
Нильпотентная группа — группа, обладающая центральным рядом подгрупп. Минимальная из длин таких рядов называется её классом нильпотентности.
Норма группы — совокупность элементов группы, перестановочных со всеми подгруппами, то есть пересечение нормализаторов всех её подгрупп.
Нормализатор подгруппы H в G — это максимальная подгруппа G, в которой H нормальна. Иначе говоря, нормализатор есть стабилизатор H при действии G на множестве своих подгрупп сопряжениями, то есть
Нормальная подгруппа (инвариантная подгруппа, нормальный делитель). H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если 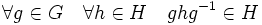
Период группы ― наименьшее общее кратное порядков элементов данной группы.
Периодическая группа ― группа, каждый элемент которой имеет конечный порядок.
Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.
Подгруппа кручения см. кручение.
Для произвольного подмножества S в G, обозначает наименьшую подгруппу G, содержащую S.
Полупрямое произведение групп G и H над гомоморфизмом 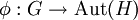
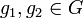
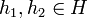
Порядок группы (G,*) — мощность G (то есть число её элементов).
Порядок элемента g группы G — минимальное натуральное число m такое, что g m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.
Простая группа — группа, в которой нет нормальных подгрупп, кроме тривиальной <e> и всей группы.
Примарная группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о p-группе.
Расширение группы — группа, содержащая данную группу в качестве нормальной подгруппы.
Разрешимая группа — группа, обладающая нормальным рядом подгрупп с абелевыми факторами. Наименьшая из длин таких рядов называется её ступенью разрешимости.
Ряд подгрупп — конечная последовательность подгрупп G0,G1. Gn называется рядом подгрупп, если 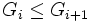
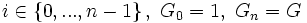
Сверхразрешимая группа — группа, обладающая нормальным рядом подгрупп с циклическими факторами.
Свободная группа, порождённая множеством A — это группа, порождённая элементами этого множества и не имеющая никаких соотношений, кроме соотношений, определяющих группу. Все свободные группы, порождённые равномощными множествами, изоморфны.
Соотношение — тождество, которому удовлетворяют образующие группы (при задании группы образующими и соотношениями).
Факторгруппа группы G по нормальной подгруппе H есть множество классов смежности подгруппы H с умножением, определяемым следующим образом:
Факторы субнормального ряда — фактор-группы Gi + 1 / Gi в определении субнормального ряда подгрупп.
Холлова подгруппа — подгруппа, порядок которой взаимно прост с её индексом во всей группе.
Центр группы G, обычно обозначается Z(G), определяется как
Z(G) = <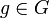
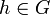
иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым элементом G.
Централизатор элемента есть максимальная подгруппа, коммутирующая с этим элементом.
Центральный ряд подгрупп — нормальный ряд подгрупп, в котором 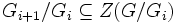
Циклическая группа — группа, состоящая из порождающего элемента и всех его целых степеней. Конечна в случае, если порядок порождающего элемента конечен.
Ядро гомоморфизма — прообраз нейтрального элемента при гомоморфизме. Ядро всегда есть нормальная подгруппа, более того, любая нормальная подгруппа есть ядро некоторого гомоморфизма.
Литература
Полезное
Смотреть что такое «Порядок элемента» в других словарях:
Порядок элемента группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Порядок — в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо, а также: порядок в физике расположение атомов, обладающее некоторой инвариантностью относительно сдвига; порядок в биологии один… … Википедия
Порядок (математика) — Порядок в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо. Специализированные варианты использования слова: Порядок (физика) Порядок (биология) Математика Порядок величины количество цифр в числе. О … Википедия
Порядок группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Порядок (матем.) — Порядок (математический), числовая характеристика математических объектов. 1) П. алгебраической кривой F (х, у) = 0, где F (х, у) ‒ многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс ═есть кривая второго П.,… … Большая советская энциклопедия
Порядок старшинства — Порядок старшинства иерархический порядок, по которому элемент или лицо располагается по отношению к другим элементам или лицам. Это может быть порядок лиц во время официальных церемоний (например, в присутствии королевской семьи) или… … Википедия
ПОРЯДОК — 1) П. алгебраич. кривой F( х, y)=0, где F( х, у) многочлен от хи у, наз. наивысшую степень членов этого многочлена. Напр., эллипс + =1 есть кривая второго П., а лемниската ( х 2+y2)2=а 2 ( х 2 у 2) кривая четвертого П. 2) П. бесконечно малой… … Математическая энциклопедия
Порядок — I Порядок (математический) числовая характеристика математических объектов. 1) П. алгебраической кривой F (х, у) = 0, где F (х, у) многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс х2 + у2)2 … Большая советская энциклопедия
ГОСТ Р 40.003-2000: Система сертификации ГОСТ Р. Регистр систем качества. Порядок проведения сертификации систем качества и сертификации производств — Терминология ГОСТ Р 40.003 2000: Система сертификации ГОСТ Р. Регистр систем качества. Порядок проведения сертификации систем качества и сертификации производств оригинал документа: 3.18 дефектоносный технологический процесс (операция):… … Словарь-справочник терминов нормативно-технической документации
ДАЛЬНИЙ ПОРЯДОК И БЛИЖНИЙ ПОРЯДОК — ДАЛЬНИЙ ПОРЯДОК И БЛИЖНИЙ ПОРЯДОК, наличие пространственной корреляции микроструктуры вещества: корреляция в пределах всего микроскопического образца дальний порядок; корреляция в области с конечным радиусом ближний порядок. То есть дальний… … Энциклопедический словарь
Порядок элемента
Имеется в виду аддитивная группа? (Если модуль m не является простым
числом, то говорить о мультипликативной группе мы не можем.)
Аддитивная группа кольца вычетов по модулю m — циклическая,
в ней есть элементы порядка m, но могут быть и элементы
меньшего порядка, их порядки должны быть делителями числа m.
Но только если модуль составной, то это всё-таки не группа.
(Но можно рассмотреть группу обратимых элементов.)
Игорь? А можно ли задать Вам вопрос?
Почему Вы не можете сразу написать всю задачу целиком?
Вы уже написали три поста, а что дано, что требуется, до сих пор не ясно.
Есть методы «умно-переборные», основанные на теор. Лагранжа: порядок элемента делит порядок группы. Если известно разложение порядка группы на множители — перебор можно существенно сократить.
Универсального непереборного метода нет. Наверное, его и вообще быть не может.
Задайте свой вопрос по математике
профессионалам
Другие вопросы на эту тему:
Порядок элемента группы
Линейная алгебра
Теория групп — не могу решить задачу
Помогите, плз, с задачей.
Доказать, что конечное множество перестановок А является группой относительно операции умножения перестановок, если произведение любой пары элементов из А принадлежит А.
С ассоцитивностью понятно все. Она наследуется из группы перестановок.
Не понимаю, как просто из того, что А замкнуто относительно операции умножения, взять нейтральный и обратный элементы.
Теорема Лагранжа утверждает, что для любой подгруппы H группы G порядок подгруппы делит порядок группы: | H | является делителем | G |. В частности, порядок | а | любого элемента является делителем | G |,
СОДЕРЖАНИЕ
Пример
| • | е | s | т | ты | v | ш |
|---|---|---|---|---|---|---|
| е | е | s | т | ты | v | ш |
| s | s | е | v | ш | т | ты |
| т | т | ты | е | s | ш | v |
| ты | ты | т | ш | v | е | s |
| v | v | ш | s | е | ты | т |
| ш | ш | v | ты | т | s | е |
Порядок и структура
2 + 2 + 2 знак равно 6 ≡ 0 ( мод 6 ) <\ Displaystyle 2 + 2 + 2 = 6 \ эквив 0 <\ pmod <6>>> 
Связь между двумя понятиями порядка следующая: если мы напишем
Для любого целого k имеем
Если a имеет бесконечный порядок, то все ненулевые степени a также имеют бесконечный порядок. Если a имеет конечный порядок, у нас есть следующая формула для порядка степеней a :
Подсчет по порядку элементов
Относительно гомоморфизмов
Уравнение класса
Важным результатом, касающимся заказов, является уравнение классов ; он связывает порядок конечной группы G с порядком ее центра Z ( G ) и размерами ее нетривиальных классов сопряженности :
Порядок элемента группы
Для общего описания теории групп см. Группа (математика) и Теория групп.
Курсив обозначает ссылку на этот словарь.
p-группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о примарной группе. Более подробно см. в статье конечная p-группа.
Аддитивная группа кольца ― группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.
Антигомоморфизм групп — отображение групп f : (G,*) → (H,×) такое, что
для произвольных a и b в G (сравните с гомоморфизмом).
Гомоморфизм групп — отображение групп 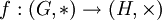
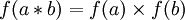
Группа Шмидта — это ненильпотентная группа, все собственные подгруппы которой нильпотентны.
Группа Миллера — Морено — это неабелева группа, все собственные подгруппы которой абелевы.
Групповая алгебра группы G над полем K — это векторное пространство над K, образующими которого являются элементы G, а умножение образующих соответсвует умножению элементов G.
Длина ряда подгрупп — число n в определении ряда подгрупп.
Изоморфизм групп — биективный гомоморфизм.
Изоморфные группы — группы, между которыми существует хотя бы один изоморфизм.
Индекс подгруппы H в группе G — число смежных классов в каждом (правом или левом) из разложений группы G по этой подгруппе H.
Индексы ряда подгрупп — индексы | Gi + 1:Gi | в определении субнормального ряда подгрупп.
Класс смежности/смежный класс (левый или правый) подгруппы H в G. Левый класс смежности элемента 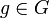
Аналогично определяется правый класс смежности:
Класс сопряжённости элемента 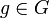
Коммутант группы есть подгруппа, порождённая всеми коммутаторами группы, обычно обозначается [G,G] или 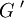
Коммутативная группа. Группа G является коммутативной, или абелевой, если её операция * коммутативна, то есть g*h=h*g 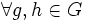
Коммутатор подгрупп — множество всевозможных произведений 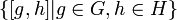
Композиционный ряд группы G — ряд подгрупп, в котором все факторы Gi + 1 / Gi — простые группы.
Конечная группа — группа с конечным числом элементов.
Конечно определённая группа — группа, обладающая конечным числом образующих и задаваемая в этих образующих конечным числом соотношений.
Конечнопорождённая группа — группа, обладающая конечной системой образующих.
Кручение, TorG, коммутативной или нильпотентной группы G есть подгруппа всех элементов конечного порядка.
Локальная теорема. Говорят, что для некоторого свойства P групп справедлива локальная теорема, если всякая группа, локально обладающая этим свойством, сама обладает им.
Например: локально абелева группа является абелевой, но локально конечная группа может быть бесконечной.
Метабелева группа ― группа, второй коммутант которой тривиален (разрешимая ступени 2).
Метациклическая группа ― группа, обладающая циклической нормальной подгруппой, факторгруппа по которой также циклическая. Всякая конечная группа, порядок которой свободен от квадратов (то есть не делится на квадрат какого-либо числа), является метациклической.
Мультипликативная группа тела ― группа, элементами которой являются все ненулевые элементы данного тела, а операция совпадает с операцией умножения в теле.
Нильпотентная группа — группа, обладающая центральным рядом подгрупп. Минимальная из длин таких рядов называется её классом нильпотентности.
Норма группы — совокупность элементов группы, перестановочных со всеми подгруппами, то есть пересечение нормализаторов всех её подгрупп.
Нормализатор подгруппы H в G — это максимальная подгруппа G, в которой H нормальна. Иначе говоря, нормализатор есть стабилизатор H при действии G на множестве своих подгрупп сопряжениями, то есть
Нормальная подгруппа (инвариантная подгруппа, нормальный делитель). H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если 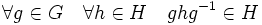
Период группы ― наименьшее общее кратное порядков элементов данной группы.
Периодическая группа ― группа, каждый элемент которой имеет конечный порядок.
Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.
Подгруппа кручения см. кручение.
Для произвольного подмножества S в G, обозначает наименьшую подгруппу G, содержащую S.
Полупрямое произведение групп G и H над гомоморфизмом 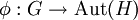
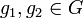
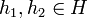
Порядок группы (G,*) — мощность G (то есть число её элементов).
Порядок элемента g группы G — минимальное натуральное число m такое, что g m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.
Простая группа — группа, в которой нет нормальных подгрупп, кроме тривиальной <e> и всей группы.
Примарная группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о p-группе.
Расширение группы — группа, содержащая данную группу в качестве нормальной подгруппы.
Разрешимая группа — группа, обладающая нормальным рядом подгрупп с абелевыми факторами. Наименьшая из длин таких рядов называется её ступенью разрешимости.
Ряд подгрупп — конечная последовательность подгрупп G0,G1. Gn называется рядом подгрупп, если 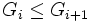
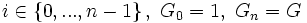
Сверхразрешимая группа — группа, обладающая нормальным рядом подгрупп с циклическими факторами.
Свободная группа, порождённая множеством A — это группа, порождённая элементами этого множества и не имеющая никаких соотношений, кроме соотношений, определяющих группу. Все свободные группы, порождённые равномощными множествами, изоморфны.
Соотношение — тождество, которому удовлетворяют образующие группы (при задании группы образующими и соотношениями).
Факторгруппа группы G по нормальной подгруппе H есть множество классов смежности подгруппы H с умножением, определяемым следующим образом:
Факторы субнормального ряда — фактор-группы Gi + 1 / Gi в определении субнормального ряда подгрупп.
Холлова подгруппа — подгруппа, порядок которой взаимно прост с её индексом во всей группе.
Центр группы G, обычно обозначается Z(G), определяется как
Z(G) = <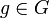
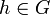
иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым элементом G.
Централизатор элемента есть максимальная подгруппа, коммутирующая с этим элементом.
Центральный ряд подгрупп — нормальный ряд подгрупп, в котором 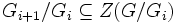
Циклическая группа — группа, состоящая из порождающего элемента и всех его целых степеней. Конечна в случае, если порядок порождающего элемента конечен.
Ядро гомоморфизма — прообраз нейтрального элемента при гомоморфизме. Ядро всегда есть нормальная подгруппа, более того, любая нормальная подгруппа есть ядро некоторого гомоморфизма.
Литература
Полезное
Смотреть что такое «Порядок элемента группы» в других словарях:
Порядок элемента — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Порядок — в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо, а также: порядок в физике расположение атомов, обладающее некоторой инвариантностью относительно сдвига; порядок в биологии один… … Википедия
Порядок (математика) — Порядок в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо. Специализированные варианты использования слова: Порядок (физика) Порядок (биология) Математика Порядок величины количество цифр в числе. О … Википедия
Порядок группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
ПОРЯДОК — 1) П. алгебраич. кривой F( х, y)=0, где F( х, у) многочлен от хи у, наз. наивысшую степень членов этого многочлена. Напр., эллипс + =1 есть кривая второго П., а лемниската ( х 2+y2)2=а 2 ( х 2 у 2) кривая четвертого П. 2) П. бесконечно малой… … Математическая энциклопедия
Порядок (матем.) — Порядок (математический), числовая характеристика математических объектов. 1) П. алгебраической кривой F (х, у) = 0, где F (х, у) ‒ многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс ═есть кривая второго П.,… … Большая советская энциклопедия
Группы симметрии — Группа симметрии (группа симметрий) некоторого объекта, многогранника или множества точек из метрического пространства ― это группа всех движений, для которых данный объект является инвариантом, с композицией в качестве групповой операции. Как… … Википедия
Порядок — I Порядок (математический) числовая характеристика математических объектов. 1) П. алгебраической кривой F (х, у) = 0, где F (х, у) многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс х2 + у2)2 … Большая советская энциклопедия
Изоморфные группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Кручение группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия