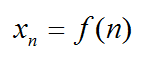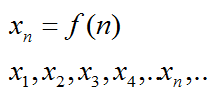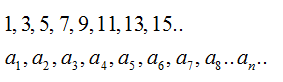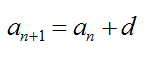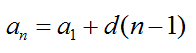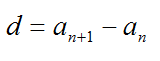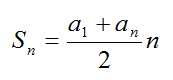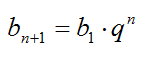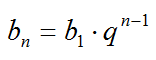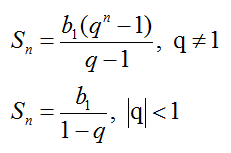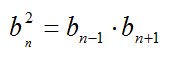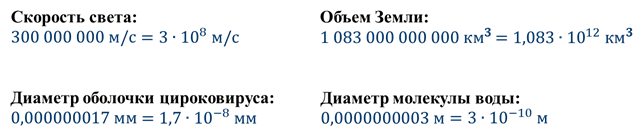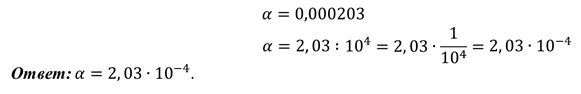Что такое порядок в алгебре
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Числовые последовательности для чайников: определение, формулы
По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.
Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.
Последовательности чисел
Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.
Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.
Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.
Что такое числовая последовательность?
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.
На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.
Какие бывают последовательности
Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.
Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Посмотрим на числа:
Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.
Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:
Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.
Сумма первых n членов прогрессии вычисляется по формуле:
Также африфметическая прогрессия обладает характреристическим свойством:
Геометрическая прогрессия
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:
Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:
Сумма первых n членов прогрессии:
Характеристическое свойство геометрической прогрессии:
Способы задания последовательностей
Последовательность можно задать несколькими способами:
Предел последовательности
Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.
Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.
Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.
Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.
Что нужно помнить, вычисляя пределы последовательностей
Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.
Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.
Стандартный вид числа
Урок 36. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Стандартный вид числа»
Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Стандартным видом числа 
называют его запись в виде: 
, где 
и 
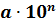
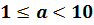
– целое число.
Число называется порядком числа .
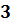
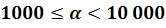
Если порядок числа равен 
, то это означает, что 
.
Если порядок числа равен 
, то это означает, что 
.
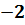
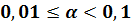
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
, где и – целое число
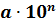
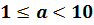
По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2. полученное число умножить на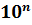 
, где подбирается так, чтобы произведение было равно данному числу.
Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Задание: запишите число в стандартном виде.
Задание: запишите в стандартном виде число, равное значению произведения х и у.
Стандартным видом числа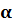 
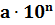
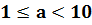
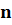
называют его запись в виде: 
, где 
и 
– целое число.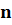
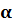
Число называется порядком числа .
Для того, чтобы привести число к стандартному виду, надо перенести в нём запятую так, чтобы она была сразу после первой значащей цифры, и полученное число умножить на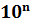 
, где подбирается так, чтобы произведение было равно данному числу.
Урок алгебры в 8-м классе по теме «Стандартный вид числа» с использованием регионального компонента
Разделы: Математика
Сторона любимая, приметная,
У тебя есть приметы предметные.
Только вот им верить не приходится-
Все они изменчивы, как водится.
Где-то есть такие ж кедры с соснами,
Где-то есть такие ж зимы с вёснами,
Горы есть со снеговыми шапками
И посёлки с трубами и шахтами.
Только нет нигде чего-то главного.
По цене одной лишь жизни равного,
Очень близкого чего-то очень местного,
Сердцу только одному известного.
Стоит лишь откуда-то вернуться,
Как готово сердце захлебнуться,
Весь мой век такое с ним случается.
Пробовал унять – не получается.
Виктор Баянов, известный кузбасский поэт.
ХОД УРОКА
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
УЧИТЕЛЬ: Здравствуйте, ребята! Вы, наверное, обратили внимание, что на доске записано стихотворение. Это необычно? Конечно! Но и урок у нас сегодня немного необычный. Мы будем изучать новый материал по алгебре, используя данные о нашем родном крае – Кемеровской области, где мы живём и учимся. (Учитель читает стихотворение кузбасского поэта В. Баянова, являющиеся эпиграфом данного урока.)
Но прежде, чем переходить к новой теме, предлагаю вам провести гимнастику для ума – поработать устно: вспомнить изученные правила, посчитать и подготовиться к знакомству с новой темой.
2. УСТНАЯ РАБОТА.
3). Вычислите: а) 3,2 * 10; б) 0,032 * 100;
в) 0,032*1000; г) 32,3 : 10; д) 32,3 : 100; е) 32,3 : 1000.
3. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.
Рассмотрим некоторые примеры (учитель записывает подробно на доске, объясняет запись, прибегает к помощи обучающихся. Обучающиеся записывают в тетрадях, внимательно слушают, задают вопросы по ходу решения и отвечают на вопросы педагога).
4. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО В ХОДЕ ВЫПОЛНЕНИЯ УПРАЖНЕНИЙ.
(Учитель готовит плакаты формата А4 с записанными на них данными по Кемеровской области. С помощью магнитов плакаты поочередно вывешиваются на доску. После записи очередного числа плакат убирается и заменяется следующим. Картинки с изображением животных и птиц вывешиваются на доску вместе с числом. Учитель комментирует плакаты, появляющиеся на доске. Картинки с изображением птиц и животных можно позаимствовать у учителя биологии или скачать из интернета, привлечь к работе можно учащихся 8 класса по желанию. Из опыта работы хочу сказать, что желающих бывает много, но необходимо помнить и об исполнительской дисциплине каждого ученика. Выполнение задания лучше проверить заранее, чтобы избежать срыва урока).
ПРИМЕР 1. Представьте в стандартном виде следующие величины:
ПРИМЕР 2. Прочтите числа, записанные в стандартном виде:
ЗАДАНИЕ: Представьте указанные данные в стандартном виде. Отметьте в таблице ответы и буквы, им соответствующие. Оставшиеся буквы зачеркните и прочтите название самой крупной из осёдлых птиц Кемеровской области, которая весит до 5 кг.
Что значит «на порядок больше»?
Часто говорят «на порядок больше», «на порядок меньше» или даже «больше/меньше на несколько порядков». Интуитивно понятно, что «на порядок больше» означает «сильно больше», «значительно больше» — но вот хотелось бы знать, на сколько именно? Если прочитаете эту статью, будете знать точно.
Любое действительное число… Простите… Возможно, не все помнят, что это такое. А знаете — неважно. Как сказал дядюшка Мерфи: «Если вы не понимаете какой-либо термин в технической статье или документации, смело его пропускайте — статья полностью сохранит свой смысл и без этого термина».
Ноль, кстати, невозможно записать таким способом, потому что мантисса, по определению, не ноль, а десятку в какую целую степень ни возводи, всё равно получится число, большее ноля, а произведение двух чисел, не равных нулю, не равно нулю.
Такой вид записи числа называют научным или стандартным. Он удобен, например, тем, что числа, записанные в такой нотации, удобно сравнивать: если числа имеют один и тот же знак (оба положительные или оба отрицательные), то сначала сравниваются экспоненты, и только потом, если экспоненты равны, сравниваются мантиссы.
Подумаешь, скажете вы, открыл Америку! И так понятно: смотрим, какое число «длиннее» — то и больше! В общем — да. Интуитивно данное понятие уже входило в круг ваших понятий, в этой статье мы просто оформили их и придали им большую чёткость.
Ещё парочка примеров:
пять миллиардов на три порядка больше семи миллионов;
скорость чтения/записи данных на жёсткий диск (миллисекунды, 10^(-3)) на три порядка меньше скорости доступа к оперативной памяти (микросекунды, 10^(-6)).
Вот, в первом приближении, и всё. Теперь вы можете с уверенностью щеголять этим термином. Или просто употреблять его грамотно и к месту. Последнее, пожалуй, предпочтительнее.
Почему «в первом приближении»? Хм… Есть довольно известная в кругах программистов шутка: для программиста «на порядок» означает «в два раза». Почему в два? Мы же только что рассказали, что «на порядок» — это «в десять раз»? Как вам сказать… Есть один нюанс. Но это уже тема другого разговора.