Что такое постфиксная форма в информатике
Польская нотация или как легко распарсить алгебраическое выражение
Введение
Перед прочтением рекомендуется прочитать следующее:
Префиксная, инфиксная и постфиксная формы
Префиксная же форма представляет из себя выражение, в котором операторы находятся перед операндами:
Соответственно, постфиксная форма представляет из себя выражение, в котором оператор находится после операндов:
Для вычисления выражения, записанного в инфиксной формы, необходимо его предварительно проанализировать с учётом старшинства операторов и скобок. В свою очередь, префиксная и постфиксная формы такого не требуют, так как операторы записываются в порядке их вычисления и без скобок.
Более подробно об представленных формах записи алгебраических выражений можно прочитать в Википедии.
Алгоритм Дейкстра
Для преобразования в постфиксную форму будем использовать улучшенный Эдсгером Вибе Дейкстрой алгоритм.
Принцип работы алгоритма Дейкстра:
Проходим исходную строку;
При нахождении числа, заносим его в выходную строку;
При нахождении оператора, заносим его в стек;
Выталкиваем в выходную строку из стека все операторы, имеющие приоритет выше рассматриваемого;
При нахождении открывающейся скобки, заносим её в стек;
При нахождении закрывающей скобки, выталкиваем из стека все операторы до открывающейся скобки, а открывающуюся скобку удаляем из стека.
Реализация алгоритма Дейкстры
В поле operationPriority скобка (‘(‘) определена лишь для того, чтобы затем не выдавало ошибки при парсинге, а тильда (‘
‘) добавлена для упрощения последующего разбора и представляет собой унарный минус.
Алгоритм вычисления постфиксной записи
После получения постфиксной записи, необходимо вычислить её значение. Для этого воспользуемся алгоримом очень похожим на прошлый алгоритмом, только этот будет использовать всего один стек.
Разберём принцип работы данного алгоритма:
Проходим постфиксную запись;
При нахождении числа, парсим его и заносим в стек;
Последнее значение, после отработки алгоритма, является решением выражения.
Реализация алгоритма вычисления постфиксной записи
Испытание алгоритмов
Попробуем пропустить выражение 15/(7-(1+1))*3-(2+(1+1))*15/(7-(200+1))3-(2+(1+1))(15/(7-(1+1))*3-(2+(1+1))+15/(7-(1+1))*3-(2+(1+1))) через составленный алгоритм и посмотрим, верно ли он работает. Для ориентирования ниже представлен вариант решения от Яндекса.

Запустив данный код, мы получим следующее:

Итоги
Хоть реализованные здесь алгоритмы и работают, однако тут не учтены пробелы между символами, дробные значения, проверка на нуль в операции деления, не реализованы функции и тому подобное, поэтому данный код предствален лишь как пример.
Рекомендуется прочитать эту статью. В данной статье автор рассказывает, как реализовать полноценный интерпретатор математических выражений с поддержкой переменных, констант и функций. Однако в этой статье автор строит интерпретатор с использованием анализатора и парсера.
Инфиксные, префиксные и постфиксные выражения¶
Когда вы записываете арифметическое выражение вроде B * C, то его форма предоставляет вам достаточно информации для корректной интерпретации. В данном случае мы знаем, что переменная B умножается на переменную C, поскольку оператор умножения * находится в выражении между ними. Такой тип записи называется инфиксной, поскольку оператор расположен между (in between) двух операндов, с которыми он работает.
Рассмотрим другой инфиксный пример: A + B * C. Операторы + и * по-прежнему располагаются между операндами, но тут уже есть проблема. С какими операндами они будут работать? + работает с A и B или * принимает B и C? Выражение выглядит неоднозначно.
Фактически, вы можете читать и писать выражения такого типа долгое время, и они не будут вызывать у вас вопросов. Причина в том, что вы кое-что знаете о + и *. Каждый оператор имеет свой приоритет. Операторы с высоким приоритетом используются прежде операторов с низким. Единственной вещью, которая может изменить порядок приоритетов, являются скобки. Для арифметических операций умножение и деление стоят выше сложения и вычитания. Если появляются два оператора одинакового приоритета, то используются порядок слева направо или их ассоциативность.
Давайте интерпретируем вызвавшее затруднение выражение A + B * C, используя приоритет операторов. B и C перемножаются первыми, затем к результату добавляется A. (A + B) * C заставит выполнить сложение A и B перед умножением. В выражении A + B + C по очерёдности (через ассоциативность) первым будет вычисляться самый левый +.
Хотя это и может быть очевидным для вас, помните, что компьютер нуждается в точном знании того, как и в какой последовательности вычисляются операторы. Одним из способов записи выражения, гарантирующим, что не возникнет путаницы по отношению к порядку операций, является создание того, что называется выражением с полностью расставленными скобками. Такой тип выражения использует пару скобок для каждого оператора. Скобки диктуют порядок операций, так что здесь не возникает многозначности. Так же отпадает необходимость помнить правила расстановки приоритетов.
Выражение A + B * C может быть переписано как ((A + (B * C)) + D) с целью показать, что умножение происходит в первую очередь, а затем следует крайнее левое сложение. A + B + C + D перепишется в (((A + B) + C) + D), поскольку операции сложения ассоциируются слева направо.
Существует ещё два очень важных формата выражений, которые на первый взгляд могут показаться вам неочевидными. Рассмотрим инфиксную запись A + B. Что произойдёт, если мы поместим оператор перед двумя операндами? Результирующее выражение будет + A B. Также мы можем переместить оператор в конец, получив A B +. Всё это выглядит несколько странным.
A + B * C можно переписать как + A * B C в префиксной нотации. Оператор умножения ставится непосредственно перед операндами B и C, указывая на приоритет * над +. Затем следует оператор сложения перед A и результатом умножения.
В постфиксной записи выражение выглядит как A B C * +. Порядок операций вновь сохраняется, поскольку * находится непосредственно после B и C, обозначая, что он имеет приоритет выше следующего +. Хотя операторы перемещаются и теперь находятся до или после соответствующих операндов, порядок последних по отношению друг к другу остаётся в точности таким, как был.
| Инфиксная запись | Префиксная запись | Постфиксная запись |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
А сейчас рассмотрим инфиксное выражение (A + B) * C. Напомним, что в этом случае запись требует наличия скобок для указания выполнить сложение перед умножением. Однако, когда A + B записывается в префиксной форме, то оператор сложения просто помещается перед операндами: + A B. Результат этой операции является первым операндом для умножения. Оператор умножения перемещается в начало всего выражения, давая нам * + A B C. Аналогично, в постфиксной записи A B + явно указывается, что первым происходит сложение. Умножение может быть выполнено для получившегося результата и оставшегося операнда C. Соответствующим постфиксным выражением будет A B + C *.
Рассмотрим эти три выражения ещё раз (см. Таблицу 3). Происходит что-то очень важное. Куда ушли скобки? Почему они не нужны нам в префиксной и постфиксной записи? Ответ в том, что операторы больше не являются неоднозначными по отношению к своим операндам. Только инфиксная запись требует дополнительных символов. Порядок операций внутри префиксного и постфиксного выражений полностью определён позицией операторов и ничем иным. Во многом именно это делает инфиксную запись наименее желательной нотацией для использования.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| (A + B) * C | * + A B C | A B + C * |
Таблица 4 демонстрирует некоторые дополнительные примеры инфиксных выражений и эквивалентных им префиксных и постфиксных записей. Убедитесь, что вы понимаете, почему они эквивалентны с точки зрения порядка выполнения операций.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| A + B * C + D | + + A * B C D | A B C * + D + |
| (A + B) * (C + D) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
Преобразование инфиксного выражения в префиксное и постфиксное¶
До сих пор мы использовали специальные методы для преобразования между инфиксными выражениями и эквивалентными им префиксной и постфикской записями. Как вы можете ожидать, существуют алгоритмические способы выполнения таких преобразований, позволяющие корректно трансформировать любое выражение любой сложности.
Первой из рассматриваемых нами техник будет использование идеи полной расстановки скобок в выражении, рассмотренной нами ранее. Напомним, что A + B * C можно записать как (A + (B * C)), чтобы явно показать приоритет умножения перед сложением. Однако, при более близком рассмотрении вы увидите, что каждая пара скобок также отмечает начало и конец пары операндов с соответствующим оператором по середине.
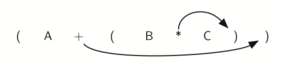
Взгляните на правую скобку в подвыражении (B * C) выше. Если мы передвинем символ умножения с его позиции и удалим соответствующую левую скобку, получив B C *, то полученный эффект конвертирует подвыражение в постфиксную нотацию. Если оператор сложения тоже передвинуть к соответствующей правой скобке и удалить связанную с ним левую скобку, то результатом станет полное постфиксное выражение (см. Изображение 6).
Рисунок 6: Перемещение операторов вправо для постфиксной записи
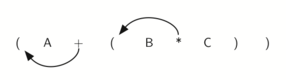
Если мы сделаем тоже самое, но вместо передвижения символа на позицию к правой скобке, сдвинем его к левой, то получим префиксную нотацию (см. Рисунок 7). Позиция пары скобок на самом деле является ключом к окончательной позиции заключённого между ними оператора.
Рисунок 7: Перемещение операторов влево для префиксной записи.
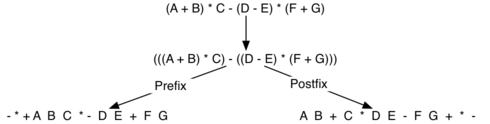
Рисунок 8: Преобразование сложного выражения к префиксной и постфиксной записи.
Обобщённое преобразование из инфиксного в постфиксный вид¶
Нам необходимо разработать алгоритм преобразования любого инфиксного выражения в постфиксное. Для этого посмотрим ближе на сам процесс конвертирования.
Рассмотрим ещё раз выражение A + B * C. Как было показано выше, его постфиксным эквивалентом является A B C * +. Мы уже отмечали, что операнды A, B и C остаются на своих местах, а местоположение меняют только операторы. Ещё раз взглянем на операторы в инфиксном выражении. Первым при проходе слева направо нам попадётся +. Однако, в постфиксном выражении + находится в конце, так как следующий оператор, *, имеет приоритет над сложением. Порядок операторов в первоначальном выражении обратен результирующему постфиксному выражению.
В процессе обработки выражения операторы должны где-то храниться, пока не найден их соответствующий правый операнд. Также порядок этих сохраняемых операторов может быть обратным (из-за их приоритета). Это случай со сложением и умножением в данном примере. Поскольку оператор сложения, появляющийся перед оператором умножения, имеет более низкий приоритет, то он должен появиться после использования оператора умножения. Из-за такого обратного порядка имеет смысл рассмотреть использование стека для хранения операторов до тех пор, пока они не понадобятся.
Что насчёт (A + B) * C? Напомним, что его постфиксный эквивалент A B + C *. Повторимся, что обрабатывая это инфиксное выражение слева направо, первым мы встретим +. В этом случае, когда мы увидим *, + уже будет помещён в результирующее выражение, поскольку имеет преимущество над * в силу использования скобок. Теперь можно начать рассматривать, как будет работать алгоритм преобразования. Когда мы видим левую скобку, мы сохраняем её как знак, что должен будет появиться другой оператор с высоким приоритетом. Он будет ожидать, пока не появится соответствующая правая скобка, чтобы отметить его местоположение (вспомните технику полной расстановки скобок). После появления правой скобки оператор выталкивается из стека.
Поскольку мы сканируем инфиксное выражение слева направо, то будем использовать стек для хранения операторов. Это предоставит нам обратный порядок, который мы отмечали в первом примере. На вершине стека всегда будет последний сохранённый оператор. Когда бы мы не прочитали новый оператор, мы должны сравнить его по приоритету с операторами в стеке (если таковые имеются).
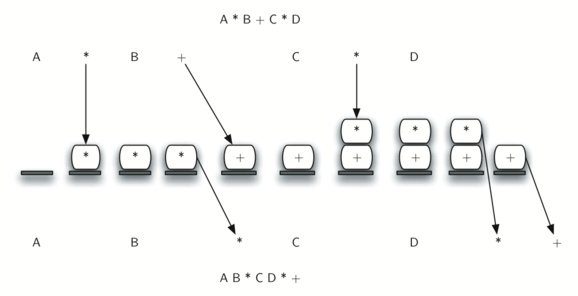
Рисунок 9 демонстрирует алгоритм преобразования, работающий над выражением A * B + C * D. Заметьте, что первый оператор * удаляется до того, как мы встречаем оператор +. Также + остаётся в стеке, когда появляется второй *, поскольку умножение имеет приоритет перед сложением. В конце инфиксного выражения из стека дважды происходит выталкивание, удаляя оба оператора и помещая + как последний элемент в результирующее постфиксное выражение.
Рисунок 9: Преобразование A * B + C * D в постфиксную запись
Для того, чтобы закодировать алгоритм на Python, мы будем использовать словарь под именем prec для хранения значений приоритета операторов. Он связывает каждый оператор с целым числом, которые можно сравнивать с другими операторами как уровень приоритетности (мы произвольно выбрали для этого целые числа 3, 2 и 1). Левая скобка получит самое низкое значение. Таким образом, любой сравниваемый с ней оператор будет иметь приоритет выше и располагаться над ней. Строка 15 определяет, что операнды могут быть любыми символами в верхнем регистре или цифрами. Полная функция преобразования показана в ActiveCode 8.
Постфиксные выражения
Постфиксные выражения состоят из основных выражений или выражений, в которых постфиксные операторы следуют за основным выражением. Постфиксные операторы перечислены в следующей таблице.
Постфиксные операторы
| Имя оператора | Нотация оператора |
|---|---|
| Оператор индекса | [ ] |
| Оператор вызова функции | ( ) |
| Оператор явного преобразования типа | Type-Name() |
| Оператор доступа к элементу | . или — |
| Постфиксный оператор приращения | ++ |
| Постфиксный оператор уменьшения | — |
Следующий синтаксис описывает возможные постфиксные выражения:
Постфиксное выражение выше может быть основным выражением или другим постфиксным выражением. Постфиксные выражения группируются слева направо, делая возможным следующее связывание выражений.
В приведенном выше выражении является первичным выражением, является постфиксным выражением func func(1) функции, func(1)->GetValue является постфиксным выражением, определяющим член класса, func(1)->GetValue() является выражением постфикса функции, а все выражением является постфиксное выражение, увеличивающее возвращаемое значение GetValue. Значение выражения в целом имеет следующий смысл: «вызовите функцию, передающую 1 в качестве аргумента, и получите указатель на класс в качестве возвращаемого значения. Затем вызовите GetValue() для этого класса, а затем увеличьте возвращаемое значение.
Перечисленные выше выражения — это выражения присваивания, что означает, что результат этих выражений должен представлять собой r-значение.
Форма постфиксного выражения
показывает вызов конструктора. Если simple-type-name — это фундаментальный тип, список выражений должен представлять собой отдельное выражение, и это выражение обозначает приведение значения выражения к фундаментальному типу. Данный тип выражения приведения копирует конструктор. Поскольку эта форма позволяет создавать фундаментальные типы и классы с использованием одного и того же синтаксиса, эта форма особенно полезна при определении шаблонных классов.
typeid Оператор считается постфиксным выражением. См. раздел оператор typeid.
Формальные и фактические аргументы
Вызов программ передает сведения в вызывающие функции в «фактических аргументах». Вызываемые функции обращаются к информации с помощью соответствующих «формальных аргументов».
При вызове функции выполняются следующие задачи.
Вычисляются все фактические аргументы (предоставляемые вызывающим объектом). Эти аргументы вычисляются в произвольном порядке, но все аргументы вычисляются и все побочные эффекты завершаются перед переходом в функцию.
Каждый формальный аргумент инициализируется с соответствующим фактическим аргументом в списке выражений. (Формальный аргумент — это аргумент, объявленный в заголовке функции и используемый в теле функции.) Преобразования выполняются таким же образом как при инициализации: стандартные и пользовательские преобразования выполняются при преобразовании фактического аргумента в требуемый тип. В общем виде выполненная инициализация показана в следующем коде.
Ниже представлены концептуальные инициализации до вызова.
Обратите внимание, что инициализация выполняется таким образом, как если бы использовался синтаксис со знаком равенства, а не синтаксис с круглыми скобками. Копия i создается до передачи значения в функцию. (Дополнительные сведения см. в разделе инициализаторы и преобразования).
Предоставление фактического аргумента при отсутствии стандартного или пользовательского преобразования в тип формального аргумента будет ошибкой.
Выполняется вызов функции.
В следующем фрагменте программного кода показан вызов функции.
При func вызове из Main формальный параметр param1 инициализируется значением i ( i преобразуется в тип в соответствии с long правильным типом, используя стандартное преобразование), а формальный параметр param2 инициализируется значением j ( j преобразуется в тип double с помощью стандартного преобразования).
Работа с типами аргументов
Некоторые из этих понятий показаны на примере следующих функций.
Многоточие и аргументы по умолчанию
Многоточие означает, что аргументы могут быть обязательными, но число и типы не указаны в объявлении. Это обычно плохой стиль программирования на языке C++, поскольку он сводит на нет одно из преимуществ этого языка: безопасность типа. Различные преобразования применяются к функциям, объявленным с многоточием, а не к функциям, для которых известны формальный и фактический типы аргументов:
Любой signed char unsigned char signed short перечисляемый тип или, или, или unsigned short битовое поле преобразуются в signed int или unsigned int с помощью целочисленного повышения.
Любой аргумент типа класса передается по значению в виде структуры данных; копия создается путем двоичного копирования, а не путем вызова конструктора копии класса (если он имеется).
Многоточие, если используется, должен быть объявлен последним в списке аргументов. Дополнительные сведения о передаче переменного числа аргументов см. в обсуждении va_arg, va_start и va_list в справочнике по библиотеке времени выполнения.
Дополнительные сведения о аргументах по умолчанию в программировании CLR см. в разделе списки аргументов переменных (. ) (C++/CLI).
Аргументы по умолчанию позволяют задать значение, которое должен принять аргумент, если в вызове функции значение не передано. В следующем фрагменте кода показано, как работают аргументы по умолчанию. Дополнительные сведения об ограничениях на указание аргументов по умолчанию см. в разделе аргументы по умолчанию.
Инкремент и декремент в Java
Что за операторы такие, зачем им префиксная и постфиксная формы, и как вычислять сложные выражения с ними (пригодится на экзамене и собеседовании).
В программировании часто приходится выполнять операции (вычислять результат выражений), в которых переменная должна увеличиться или уменьшиться на единицу.
Программист, преподаватель Skillbox. Пишет про Java.
Пример 1
Тут всё просто, достаточно удостовериться, что значения переменных поменялись.
Примечание. Инкремент и декремент относятся к арифметическим операторам. Мы помним, что операнды арифметических операторов должны быть числового типа. Однако в Java допустим и тип char, потому что здесь это по сути разновидность типа int.
Проверим, как это работает с инкрементом и декрементом.
Пример 2
Пример 3
На каждой итерации цикла значение переменной i выводится в консоль, а сама переменная увеличивается на один после каждого витка.
Примечание: если в примере выше заменить i++ на ++i, то результат в консоли не поменяется — проверьте.
Дело в том, что преинкремент и постинкремент в условии цикла for можно сравнить с вызовом двух разных функций. Каждая из них делает одно и то же — увеличивает переменную i (после выполнения тела цикла), и только возвращаемые ими значения различаются.
Однако возвращаемое инкрементом значение в условии цикла использовать негде (нет выражения для вычисления) — поэтому оно просто выбрасывается.
Вот почему на работе цикла подобная замена не отразилась.
Пример 4
Перепишем пример с циклом так:
Как видим, вывод снова не изменился.
Всё потому, что в метод System. out.println () передаётся текущее значение переменной i, и лишь потом оно увеличивается на единицу.
За это отвечает постфиксная форма записи инкремента. А ещё есть префиксная. И для декремента тоже.
Префиксная и постфиксная формы
Синтаксис тут такой ( x — переменная):
| Операция | Постфиксная версия | Префиксная версия |
|---|---|---|
| Инкремент | x++ | ++x |
| Декремент | х— | —х |
Различия в работе:
Обратите внимание на слово потом. Потом — это когда? После вычисления всего выражения? Чтобы понять это, разберёмся с порядком вычисления инкрементов и декрементов.
Порядок вычисления выражений с операторами ++ и −−
Значения, которые инкременты возвращают в выражение, вычисляются до выполнения других операций. И то же самое для декрементов.
О приоритете и ассоциативности
Не путайте приоритет с обычным порядком выполнения операторов. Все инструкции Java выполняет в привычном нам направлении (слева направо), и операнды операторов вычисляет так же.
Приоритеты же определяют порядок выполнения операторов, которые сами являются частью более сложного (составного) арифметического или логического выражения.
Если на одном уровне встречаются операции одинакового приоритета, то какие из них выполнять первыми — определяет уже ассоциативность.
Пример 5
Разберём пример выше.
x = 3. Найдём значение выражения 2 * x++:
Значение b стало равным 4, а y равен 2.
Выражение с несколькими инкрементами/декрементами
В этом случае стоит помнить, что:
Если в выражении много инкрементов/декрементов одной переменной
Тогда входным значением переменной для вычисления каждого последующего инкремента или декремента будет значение этой переменной после вычисления предыдущего инкремента или декремента.
То есть инкременты/декременты в выражении обрабатываются не одновременно, а по очереди, порядок в которой определяется ассоциативностью и приоритетом этих операторов в Java.