Что такое постфиксная запись
Обратная польская запись
Два плюс два, умножить на два?
Не знаю как вы, но я в школе долго мучился, пытаясь разобраться с приоритетом операций и скобками. Потом, как и каждый начинающий программист, я мучился с приоритетом операций и скобками, когда писал собственный калькулятор. А оказалось, что все эти мучения были напрасны. Ведь существует прекрасный механизм, известный, как обратная польская запись. О том, что это такое и как с этим работать я и хочу вам рассказать.
В математике существует древняя традиция помещать оператор между операндами (x+y), а не после операндов (xy+). Форма с оператором между операндами называется инфиксной записью. Форма с оператором после операндов называется постфиксной, или обратной польской записью в честь польского логика Я. Лукасевича (1958), который изучал свойства этой записи.
Обратная польская запись имеет ряд преимуществ перед инфиксной записью при выражении алгебраических формул. Во-первых, любая формула может быть выражена без скобок. Во-вторых, она удобна для вычисления формул в машинах со стеками. В-третьих, инфиксные операторы имеют приоритеты, которые произвольны и нежелательны. Например, мы знаем, что ab+c значит (ab)+c, а не a(b+c), поскольку произвольно было определено, что умножение имеет приоритет над сложением. Но имеет ли приоритет сдвиг влево перед операцией И? Кто знает? Обратная польская запись позволяет устранить такие недоразумения.
Постановка задачи
На вход программы поступает выражение, состоящее из односимвольных идентификаторов и знаков арифметических действий. Требуется преобразовать это выражение в обратную польскую запись или же сообщить об ошибке.
Алгоритм перевода в обратную польскую запись
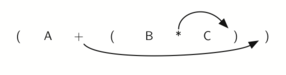
Существует несколько алгоритмов для превращения инфиксных формул в обратную польскую запись. Мы рассмотрим переработанный алгоритм, идее которого предложена Э. Дейкстра (E.W. Dijkstra). Предположим, что формула состоит из переменных, двухоперандных операторов +,-,*,/,^, а также левой и правой скобок. Чтобы отметить конец формулы, мы будем вставлять символ после её последнего символа и перед первым символом следующей формулы.
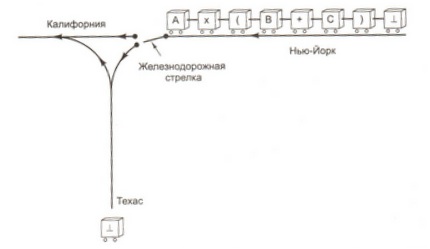
На рисунке схематично показана железная дорога из Нью-Йорка в Калифорнию с ответвлением, ведущим в Техас. Каждый символ формулы представлен одним вагоном. Поезд движется на запад (налево). Перед стрелкой каждый вагон должен останавливаться и узнавать, должен ли он двигаться прямо в Калифорнию, или ему нужно будет по пути заехать в Техас. Вагоны, содержащие переменные, всегда направляются в Калифорнию и никогда не едут в Техас. Вагоны, содержащие все прочие символы, должны перед прохождением стрелки узнавать о содержимом ближайшего вагона, отправившегося в Техас.
В таблице показана зависимость ситуации от того, какой вагон отправился в Техас последним и какой вагон находится у стрелки. Первый вагон (помеченный символом ⊥) всегда отправляется в Техас.
Числа соответствуют следующим ситуациям:
1. Вагон на стрелке отправляется в Техас
2. Последний вагон, направившийся в Техас, разворачивается и направляется в Калифорнию
3. Вагон, находящийся на стрелке, и последний вагон, отправившийся в Техас, угоняются и исчезают
4. Остановка. Символы, находящиеся на Калифорнийской ветке, представляют собой формулу в обратной польской записи, если читать слева направо
5. Остановка. Произошла ошибка. Изначальная формула была некорректно сбалансирована
После каждого действия производится новое сравнение вагона, находящегося у стрелки (это может быть тот же вагон, что и в предыдущем сравнении, а может быть следующий вагон), и вагона, который на данный момент последним ушёл на Техас. Этот процесс продолжается до тех пор, пока не будет достигнут шаг 4. Отметим, что линия на Техас используется как стек, где отправка вагона в Техас – это помещение элемента в стек, а разворот отправленного в Техас вагона в сторону Калифорнии – это выталкивание элемента из стека.
Порядок следования переменных в инфиксной и постфиксной записи одинаков. Однако порядок следования операторов не всегда один и тот же. В обратной польской записи операторы появляются в том порядке, в котором они будут выполняться.
Пример вычисления выражения в обратной польской записи
Обратная польская запись идеально подходит для вычисления формул на компьютере со стеком. Формула состоит из n символов, каждый из которых является либо операндом, либо оператором. Алгоритм для вычисления формулы в обратной польской записи с использованием стека прост. Нужно просто прочитать обратную польскую запись слева направо. Если встречается операнд, его нужно пометить в стек. Если встречается оператор, нужно выполнить заданную им операцию.
В качестве примера рассмотрим вычисление следующего выражения: (8+2*5)/(1+3*2-4). Соответствующая формула в обратной польской записи выглядит так: 825*+132*+4-/
Число на вершине стека – это правый операнд (а не левый). Это очень важно дл операций деления, вычитания и возведения в степень, поскольку порядок следования операндов в данном случае имеет значение (в отличие от операций сложения и умножения). Другими словами, операция деления действует следующим образом: сначала в стек помещается числитель, потом знаменатель, и тогда операция даёт правильный результат. Отметим, что преобразовать обратную польскую запись в машинный код очень легко: нужно просто двигаться по формуле в обратной польской записи, записывая по одной команде для каждого символа. Если символ является константой или переменной, нужно вписывать команду помещения этой константы или переменной в стек, если символ является оператором, нужно вписывать команду выполнения это операции. 
P.S. Исходные коды вы, как всегда, можете скачать на моём сайте, пока он не ляжет под хабраэффектом.
P.P.S. Теперь все могут написать свой калькулятор. С блэкджеком и скобками.
Инфиксные, префиксные и постфиксные выражения¶
Когда вы записываете арифметическое выражение вроде B * C, то его форма предоставляет вам достаточно информации для корректной интерпретации. В данном случае мы знаем, что переменная B умножается на переменную C, поскольку оператор умножения * находится в выражении между ними. Такой тип записи называется инфиксной, поскольку оператор расположен между (in between) двух операндов, с которыми он работает.
Рассмотрим другой инфиксный пример: A + B * C. Операторы + и * по-прежнему располагаются между операндами, но тут уже есть проблема. С какими именно операндами они будут работать? + работает с A и B или * принимает B и C? Выражение выглядит неоднозначно.
Фактически, вы можете читать и писать выражения такого типа долгое время, и они не будут вызывать у вас вопросов. Причина в том, что вы кое-что знаете о + и *. Каждый оператор имеет свой приоритет. Операторы с высоким приоритетом используются прежде операторов с низким. Единственной вещью, которая может изменить порядок приоритетов, являются скобки. Для арифметических операций умножение и деление стоят выше сложения и вычитания. Если появляются два оператора одинакового приоритета, то используются порядок слева направо, или их ассоциативность.
Давайте интерпретируем вызвавшее затруднение выражение A + B * C, используя приоритет операторов. B и C перемножаются первыми, затем к результату добавляется A. (A + B) * C заставит выполнить сложение A и B перед умножением. В выражении A + B + C по очерёдности (через ассоциативность) первым будет вычисляться самый левый +.
Хотя это очевидно для вас, помните: компьютер нуждается в точном знании того, как и в какой последовательности вычисляются операторы. Одним из способов записи выражения, гарантирующим, что не возникнет путаницы по отношению к порядку операций, является создание того, что называется выражением с полностью расставленными скобками. Такой тип выражения использует пару скобок для каждого оператора. Скобки диктуют порядок операций, так что здесь не возникает многозначности. Так же отпадает необходимость помнить правила расстановки приоритетов.
Выражение A + B * C + D может быть переписано как ((A + (B * C)) + D) с целью показать, что умножение происходит в первую очередь, а затем следует крайнее левое сложение. A + B + C + D перепишется в (((A + B) + C) + D), поскольку операции сложения ассоциируются слева направо.
Существует ещё два очень важных формата выражений, которые на первый взгляд могут показаться вам неочевидными. Рассмотрим инфиксную запись A + B. Что произойдёт, если мы поместим оператор перед двумя операндами? Результирующее выражение будет + A B. Также мы можем переместить оператор в конец, получив A B +. Всё это выглядит несколько странным.
A + B * C в префиксной нотации можно переписать как + A * B C. Оператор умножения ставится непосредственно перед операндами B и C, указывая на приоритет * над +. Затем следует оператор сложения перед A и результатом умножения.
В постфиксной записи выражение выглядит как A B C * +. Порядок операций вновь сохраняется, поскольку * находится непосредственно после B и C, обозначая, что он имеет приоритет выше следующего +. Хотя операторы перемещаются и теперь находятся до или после соответствующих операндов, порядок последних по отношению друг к другу остаётся в точности таким, как был.
| Инфиксная запись | Префиксная запись | Постфиксная запись |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
А сейчас рассмотрим инфиксное выражение (A + B) * C. Напомним, что в этом случае запись требует наличия скобок для указания выполнить сложение перед умножением. Однако, когда A + B записывается в префиксной форме, то оператор сложения просто помещается перед операндами: + A B. Результат этой операции является первым операндом для умножения. Оператор умножения перемещается в начало всего выражения, давая нам * + A B C. Аналогично, в постфиксной записи A B + явно указывается, что первым происходит сложение. Умножение может быть выполнено для получившегося результата и оставшегося операнда C. Соответствующим постфиксным выражением будет A B + C *.
Рассмотрим эти три выражения ещё раз (см. таблицу 3). Происходит что-то очень важное. Куда ушли скобки? Почему они не нужны нам в префиксной и постфиксной записи? Ответ в том, что операторы больше не являются неоднозначными по отношению к своим операндам. Только инфиксная запись требует дополнительных символов. Порядок операций внутри префиксного и постфиксного выражений полностью определён позицией операторов и ничем иным. Во многом именно это делает инфиксную запись наименее желательной нотацией для использования.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| (A + B) * C | * + A B C | A B + C * |
Таблица 4 демонстрирует некоторые дополнительные примеры инфиксных выражений и эквивалентных им префиксных и постфиксных записей. Убедитесь, что вы понимаете, почему они эквивалентны с точки зрения порядка выполнения операций.
| Инфиксное выражение | Префиксное выражение | Постфиксное выражение |
|---|---|---|
| A + B * C + D | + + A * B C D | A B C * + D + |
| (A + B) * (C + D) | * + A B + C D | A B + C D + * |
| A * B + C * D | + * A B * C D | A B * C D * + |
| A + B + C + D | + + + A B C D | A B + C + D + |
Преобразование инфиксного выражения в префиксное и постфиксное¶
До сих пор мы использовали специальные методы для преобразования между инфиксными выражениями и эквивалентными им префиксной и постфикской записями. Как вы можете ожидать, существуют алгоритмические способы выполнения таких преобразований, позволяющие корректно трансформировать любое выражение любой сложности.
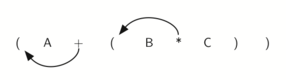
Первой из рассматриваемых нами техник будет использование идеи полной расстановки скобок в выражении, рассмотренной нами ранее. Напомним, что A + B * C можно записать как (A + (B * C)), чтобы явно показать приоритет умножения перед сложением. Однако, при более близком рассмотрении вы увидите, что каждая пара скобок также отмечает начало и конец пары операндов с соответствующим оператором по середине.
Взгляните на правую скобку в подвыражении (B * C) выше. Если мы передвинем символ умножения с его позиции и удалим соответствующую левую скобку, получив B C *, то произойдёт конвертирование подвыражение в постфиксную нотацию. Если оператор сложения тоже передвинуть к соответствующей правой скобке и удалить связанную с ним левую скобку, то результатом станет полностью постфиксное выражение (см. рисунок 6).
Рисунок 6: Перемещение операторов вправо для постфиксной записи
Если мы сделаем тоже самое, но вместо передвижения символа на позицию к правой скобке, сдвинем его к левой, то получим префиксную нотацию (см. рисунок 7). Позиция пары скобок на самом деле является ключом к окончательной позиции заключённого между ними оператора.
Рисунок 7: Перемещение операторов влево для префиксной записи.
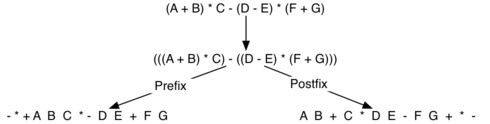
Рисунок 8: Преобразование сложного выражения к префиксной и постфиксной записи.
Обобщённое преобразование из инфиксного в постфиксный вид¶
Нам необходимо разработать алгоритм преобразования любого инфиксного выражения в постфиксное. Для этого посмотрим ближе на сам процесс конвертирования.
Рассмотрим ещё раз выражение A + B * C. Как было показано выше, его постфиксным эквивалентом является A B C * +. Мы уже отмечали, что операнды A, B и C остаются на своих местах, а местоположение меняют только операторы. Ещё раз взглянем на операторы в инфиксном выражении. Первым при проходе слева направо нам попадётся +. Однако, в постфиксном выражении + находится в конце, так как следующий оператор, *, имеет приоритет над сложением. Порядок операторов в первоначальном выражении обратен результирующему постфиксному выражению.
В процессе обработки выражения операторы должны где-то храниться, пока не найден их соответствующий правый операнд. Также порядок этих сохраняемых операторов может быть обратным (из-за их приоритета), как в данном примере со сложением и умножением. Поскольку оператор сложения, появляющийся перед оператором умножения, имеет более низкий приоритет, то он должен появиться после использования последнего. Из-за такого обратного порядка имеет смысл рассмотреть использование стека для хранения операторов до тех пор, пока они не понадобятся.
Что насчёт (A + B) * C? Напомним его постфиксный эквивалент: A B + C *. Повторимся, что обрабатывая это инфиксное выражение слева направо, первым мы встретим +. В этом случае, когда мы увидим *, + уже будет помещён в результирующее выражение, поскольку имеет преимущество над * в силу использования скобок. Теперь можно приступить к рассмотрению работы алгоритма преобразования. Когда мы видим левую скобку, то сохраняем её как знак, что должен будет появиться другой оператор с высоким приоритетом. Он будет ожидать, пока не появится соответствующая правая скобка, чтобы отметить его местоположение (вспомните технику полной расстановки скобок). После появления правой скобки оператор выталкивается из стека.
Поскольку мы сканируем инфиксное выражение слева направо, то для хранения операторов будем использовать стек. Это предоставит нам обратный порядок, который был отмечен в первом примере. На вершине стека всегда будет последний сохранённый оператор. Когда бы мы не прочитали новый оператор, мы должны сравнить его по приоритету с операторами в стеке (если таковые имеются).
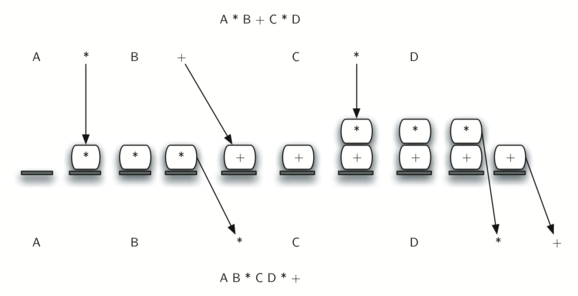
Рисунок 9 демонстрирует алгоритм преобразования, работающий над выражением A * B + C * D. Заметьте, что первый оператор * удаляется до того, как мы встречаем оператор +. Также + остаётся в стеке, когда появляется второй *, поскольку умножение имеет приоритет перед сложением. В конце инфиксного выражения из стека дважды происходит выталкивание, удаляя оба оператора и помещая + как последний элемент в результирующее постфиксное выражение.
Рисунок 9: Преобразование A * B + C * D в постфиксную запись
Чтобы закодировать алгоритм на Python, мы будем использовать словарь под именем prec для хранения значений приоритета операторов. Он связывает каждый оператор с целым числом, которые можно сравнивать с числами других операторов, как уровень приоритетности (для этого мы произвольно выбрали целые числа 3, 2 и 1). Левая скобка получит самое низкое значение. Таким образом, любой сравниваемый с ней оператор будет иметь приоритет выше и располагаться над ней. Строка 15 определяет, что операнды могут быть любыми символами в верхнем регистре или цифрами. Полная функция преобразования показана в ActiveCode 8.
Польская нотация или как легко распарсить алгебраическое выражение
Введение
Перед прочтением рекомендуется прочитать следующее:
Префиксная, инфиксная и постфиксная формы
Префиксная же форма представляет из себя выражение, в котором операторы находятся перед операндами:
Соответственно, постфиксная форма представляет из себя выражение, в котором оператор находится после операндов:
Для вычисления выражения, записанного в инфиксной формы, необходимо его предварительно проанализировать с учётом старшинства операторов и скобок. В свою очередь, префиксная и постфиксная формы такого не требуют, так как операторы записываются в порядке их вычисления и без скобок.
Более подробно об представленных формах записи алгебраических выражений можно прочитать в Википедии.
Алгоритм Дейкстра
Для преобразования в постфиксную форму будем использовать улучшенный Эдсгером Вибе Дейкстрой алгоритм.
Принцип работы алгоритма Дейкстра:
Проходим исходную строку;
При нахождении числа, заносим его в выходную строку;
При нахождении оператора, заносим его в стек;
Выталкиваем в выходную строку из стека все операторы, имеющие приоритет выше рассматриваемого;
При нахождении открывающейся скобки, заносим её в стек;
При нахождении закрывающей скобки, выталкиваем из стека все операторы до открывающейся скобки, а открывающуюся скобку удаляем из стека.
Реализация алгоритма Дейкстры
В поле operationPriority скобка (‘(‘) определена лишь для того, чтобы затем не выдавало ошибки при парсинге, а тильда (‘
‘) добавлена для упрощения последующего разбора и представляет собой унарный минус.
Алгоритм вычисления постфиксной записи
После получения постфиксной записи, необходимо вычислить её значение. Для этого воспользуемся алгоримом очень похожим на прошлый алгоритмом, только этот будет использовать всего один стек.
Разберём принцип работы данного алгоритма:
Проходим постфиксную запись;
При нахождении числа, парсим его и заносим в стек;
Последнее значение, после отработки алгоритма, является решением выражения.
Реализация алгоритма вычисления постфиксной записи
Испытание алгоритмов
Попробуем пропустить выражение 15/(7-(1+1))*3-(2+(1+1))*15/(7-(200+1))3-(2+(1+1))(15/(7-(1+1))*3-(2+(1+1))+15/(7-(1+1))*3-(2+(1+1))) через составленный алгоритм и посмотрим, верно ли он работает. Для ориентирования ниже представлен вариант решения от Яндекса.

Запустив данный код, мы получим следующее:

Итоги
Хоть реализованные здесь алгоритмы и работают, однако тут не учтены пробелы между символами, дробные значения, проверка на нуль в операции деления, не реализованы функции и тому подобное, поэтому данный код предствален лишь как пример.
Рекомендуется прочитать эту статью. В данной статье автор рассказывает, как реализовать полноценный интерпретатор математических выражений с поддержкой переменных, констант и функций. Однако в этой статье автор строит интерпретатор с использованием анализатора и парсера.
Что такое постфиксная запись
Постфиксная запись представляет собой такую запись арифметического выражения, в которой сначала записываются операнды, а затем – знак операции. Например, для выражения a + b * c постфиксная запись будет a b c * +. Здесь операндами операции * будут b и c (два ближайших операнда), а операндами операции + будут а и составной операнд b c *. Эта запись удобна тем, что она не требует скобок. Например, для выражения (a + b) * c постфиксная запись будет a b + c *. В этой записи не требуется ставить скобки для того, чтобы изменить порядок вычисления, зависящий от приоритета операций, как в исходном выражении.
Алгоритм перевода в постфиксную запись обрабатывает исходный массив лексем и строит новый массив из тех же лексем, расположенных в другом порядке. Кроме того, необходим еще стек – аналогичный массив, используемый для временного хранения операций.
Алгоритм перевода выражения в постфиксную запись следующий.
Обратите внимание, что после перекладывания операции из стека в результат при завершении работы алгоритма, порядок операций сменился на противоположный.
Расширить этот алгоритм так, чтобы он обрабатывал выражения, содержащие вызовы функций несложно. Для удобства перевода выражения в постфиксную запись в синтаксическом анализаторе необходимо в список лексем сначала класть открывающую скобку, а затем имя функции. В алгоритме перевода в постфиксную запись появляется новый пункт:
Вычислить значение выражения, записанного в постфиксной записи, очень просто (не забудьте только сначала ввести значения переменных, использованных в выражении). Просматриваем постфиксную запись. Значения переменных и констант кладутся в стек. Когда встречается операция, из стека берутся два верхних значения, вычисляется результат применения операции к этим значениям, и результат помещается в стек. Если встречается функция, то берётся одно значение из стека, а результат помещается в стек на его место.
Вычислим значение выражения a b c + * d + 2 / при а = 1, b = 2, c = 3, d = 4
| Обрабатываемая лексема | Стек |
| a | 1 |
| b | 1 2 |
| c | 1 2 3 |
| + | 1 5 |
| * | 5 |
| d | 5 4 |
| + | 9 |
| 2 | 9 2 |
| / | 4.5 |
Вычислим значение выражения x x sin 2 * + при x = 3.14
| Обрабатываемая лексема | Стек |
| x | 3.14 |
| x | 3.14 3.14 |
| sin | 3.14 0 |
| 2 | 3.14 0 2 |
| * | 3.14 0 |
| + | 3.14 |
| Обрабатываемая лексема | Стек |
| a | 0 |
| b | 0 2 |
| || | 1 |
| c | 1 0 |
| ! | 1 1 |
| && | 1 |
Файл в формате Word
Префиксная и постфиксная польская (бесскобочная) форма записи.
Обычные арифметические выражения, используемые в повседневной практике и содержащие скобки, называютинфиксными выражениями, поскольку знак операции располагается между операндами. Порядок выполнения действий в таких выражениях определяется старшинством операций и скобками. Вычисление и компиляция таких выражений подразумевает их предварительный анализ с целью выявления порядка выполнения операций. Существуют формы записи арифметических выражений без скобок, в которых порядок действий задается порядком знаков операций в выражении. Такие формы записи называются польской или бесскобочной записью. Польская запись может быть префиксной, в которой знак операции предшествует операндам, и постфиксной, в которой знак операции следует за операндом. Вычисление и компиляция бесскобочных выражений оказывается проще, чем выражений со скобками, поскольку операции должны выполняться в порядке описания и предварительный анализ не требуется.
Префиксная польская запись (ПрПЗ) определяется следующим образом.
Если инфиксное выражение Е представляет собой один операнд а, то ПрПЗ выражения Е – это просто а.
Если (Е) есть инфиксное выражение, то ПрПЗ этого выражения есть ПрПЗ Е.
Перечисленные правила определяют порядок построения ПрПЗ заданного инфиксного выражения. Например, для выражений (a + b) * (c — d) построение ПрПЗ можно выполнить так. Обозначим операнды первой выполняемой операции:
Согласно определению префиксная запись выражения Е1*Е2 – это *E1‘E2‘, где Е1‘,Е2‘ – префиксные записи выражений Е1и Е2. Выполняя построение постфиксных записей для этих выражений,
окончательно получаем результат в виде:
Постфиксная записьотличается тем, что знак операции ставится непосредственно за операндами. Так, например, инфиксной записи (A+B) соответствует постфиксная форма AB+.
Постфиксная польская запись (ПоПЗ) определяется следующим образом.
Если инфиксное выражение Е представляет собой один операнд а, то ПоПЗ выражения Е – это а.
Если (Е) есть инфиксное выражение, то постфиксная запись этого выражения есть постфиксная запись Е.
Аналогично предыдущему примеру построим ПоПЗ выражения
Обозначая операнды внешней операции
найдем постфиксные записи операндов, которые имеют вид:
Подставляя полученные постфиксные записи в выражение
Постфиксная запись выражений обладает двумя ценными свойствами, благодаря которым ее широко используют в компиляторах:
Для записи любого выражения не нужны скобки.
Так как оператор непосредственно следует за операндами, участвующими в операции, неопределенность в указании операндов отсутствует. Например, выражение (A+B)+C имеет постфиксную форму AB+C+, а выражение A+(B+C) представляется в форме ABC++.
К моменту считывания очередного оператора соответствующие операнды уже были прочитаны. Поэтому оператор может быть выполнен без считывания каких-либо дополнительных данных.
Сказанное выше относится к бинарным операциям, однако это нетрудно распространить на унарные операции. Так, унарный оператор отрицания (эту операцию будем обозначать знаком
) просто ставят непосредственно за аргументом. Например, инфиксная запись
A представляется в форме A
(Заметим, что знак «-» может стоять в инфиксной записи, указывая как бинарную, так и унарную операцию, и его правильный смысл становится очевидным из контекста. В постфиксной записи это сделать труднее.
Благодаря описанным выше свойствам выражение в постфиксной форме может быть вычислено с помощью простого алгоритма:
lex = getNextLex(); // считать следующую лексему
if(isOperand(lex)) // лексема есть операнд
push(lex); // записать лексему в стек
if(isOperator(lex)) // лексема есть оператор
push(performOperation(lex, pop(), pop()));
/* выполнить указанную лексемой операцию над последними элементами, записанными в стек, и заменить эти элементы результатом операции;
В результате вычислений значение выражения оказывается единственным элементом стека.
Такой алгоритм, выполняющий операции над стеком, лежит практически в основе любого компилятора. Обычно блок синтаксического анализа преобразует программу в постфиксную форму, после чего генератор кода строит объектную программу, просматривая выражения вышеописанным методом.
Очевидно, что вычисление постфиксной записи выражения не представляет трудности, преобразование же инфиксной записи в постфиксную заметно сложнее. Предположим, что продукция языка имеет вид
где A, B и C являются нетерминалами, а «и» – терминал. Будем считать, что знаки операций являются терминалами. Тогда эта продукция означает, что нетерминал A является инфиксной записью, в которой участвуют операнды B и C вместе с оператором «и». Следовательно, постфиксная форма выражения образуется из операндов B, C, за которыми следует оператор «и». Таким образом, для данной продукции постфиксная запись имеет вид
Постфиксная запись для B
Постфиксная запись для C
Если терминальные символы выводятся в выходной файл в таком порядке, то все фразы языка будут представлены в постфиксной форме.
Преобразование выражения из инфиксной записи в постфиксную.
Части выражения, заключенные в скобки на самом нижнем уровне скобочных вложений для данного выражения, должны быть сначала преобразованы в постфиксную форму, с тем, чтобы их можно было рассматривать как один операнд. При таком подходе преобразование всего выражения приведет к полному исключению из него скобок. Последняя открываемая в группе скобок скобочная пара содержит первое преобразуемое выражение в этой группе. Принцип «последнее открываемое выражение вычисляется первым» предполагает использование стека.
Рассмотрим два выражения в инфиксной форме: А+В*С и (А+В)*С и соответствующие им постфиксные формы АВС*+ иАВ+С*. В каждом случае порядок следования операндов в этих формах совпадает с порядком следования операндов в исходных выражениях. При просмотре первого выражения (А+В*С) первый операнд А может быть сразу же помещен в постфиксное выражение. Очевидно, что символ «+» не может быть помещен в это выражение до тех пор, пока туда не будет помещен второй, еще не просмотренный операнд. Следовательно, он (т.е. символ «+») должен быть сохранен, а впоследствии извлечен и помещен в соответствующую позицию. После просмотра операнда В этот символ записывается вслед за операндом А. К этому моменту просмотренными уже оказываются два операнда. Однако извлекать и помещать символ «+» в постфиксную запись еще рано, т.к. за ним следует символ «*», имеющий более высокий приоритет. Во втором выражении наличие скобок обуславливает выполнение операции «+» в первую очередь.
Так как при преобразовании инфиксной формы в постфиксную правила приоритета играют существенную роль, для их учета введем функцию precedence(oper1, oper2), где oper1 и oper2 – символы, обозначающие операции. Эта функция возвращает значение TRUE, если oper1 имеет более высокий приоритет, чем oper2, или они имеют равный приоритет, но oper1 располагается слева от oper2 в бесскобочном выражении, представленном в инфиксной форме. В противном случае функция precedence(oper1, oper2) возвращает значение FALSE.Например, значения функций precedence(«*»,»+») и precedence(«+» «+») – «истина», аprecedence («+»,»*») – «ложь».
Фрагмент текста в этом абзаце подчеркнут, так как неправильное формирование постфиксной записи (как вручную, так разработанными студентами программными генераторами) для операций с равным приоритетом является одной из типичных ошибок.
Рассмотрим теперь макет алгоритма для преобразования строки, представленной в инфиксной форме и не содержащей скобок, в постфиксную строку. Поскольку мы считаем, что во входной строке скобки отсутствуют, единственным признаком порядка выполнения операций является их приоритет.
1. (Установить в постфиксную строку » «);
2. (Очистить стек с именем opstk);
3. while (на входе еще имеются символы) <
6. (добавить символ к постфиксной строке);
8. while(empty(stack) == FALSE) &&
(precedence(stacktop(opstk), symb) == TRUE)) <
/* smbtp имеет приоритет больший, чем symb, поэтому она может быть добавлена к постфиксной строке. */
10. (добавить smbtp к постфиксной строке);
/* в этой точке либо opstk пуст, либо symb имеет приоритет над stacktop(opstk). Мы не можем поместить symb в постфиксную строку до тех пор, пока не считаем следующую операцию, которая может иметь более высокий приоритет. Следовательно, мы должны сохранить symb. */
/* к этому моменту строка оказывается просмотренной целиком. Мы должны поместить оставшиеся в стеке операции в постфиксную строку. */
15. while(empty(opstk) == FALSE) <
(добавить smbtp к постфиксной строке);
Для обеспечения возможности работы со скобками после считывания открывающейся скобки она записывается в стек. Это может быть выполнено путем установки правила precedence(op, «(«) == FALSE для любого символа операции, отличного от символа правой (закрывающей) скобки. Также определим precedence(«(«, op) == FALSE для того, чтобы символ операции, появляющийся после левой скобки, записывался в стек.
После считывания закрывающей скобки все операции вплоть до первой открывающей скобки должны быть прочитаны из стека и помещены в постфиксную строку. Это может быть сделано путем установки precedence(op, «)») == TRUEдля всех операций op, отличных от левой скобки. После считывания этих операций из стека и закрытия открывающей скобки необходимо выполнить следующую операцию. Открывающая скобка должна быть удалена из стека и отброшена вместе с закрывающей скобкой. Обе скобки не помещаются затем ни в постфиксную строку, ни в стек. Установим функцию precedence(«(«, «)») равной FALSE. Это гарантирует нам то, что при достижении открывающей скобки цикл, начинающийся в строке 8, будет пропущен, а открывающая скобка не будет помещена в постфиксную строку.
Выполнение продолжится со строки 12. Однако, поскольку открывающая скобка не должна помещаться в стек, строка 12 заменяется оператором
if((empty(opstk) == TRUE) || (symb <> «)»))
С учетом приведенных соглашений для функции precedence, а также исправлений для строки 12 рассмотренный алгоритм может быть использован для преобразования любой строки, записанной в инфиксной форме, в постфиксную. Подытожим правила приоритетности скобок:
precedence(«(«,op) == FALSE для любой операции op
precedence(op,»(«) == FALSE для любой операции op, отличной от «)»
precedence(op,»)») == TRUE для любой операции op, отличной от «(«
precedence(«)»,op) = «неопределенно» для любой операции op, (попытка сравнения двух указанных операций означает ошибку)
Проиллюстрируем этот алгоритм несколькими примерами:
Пример1:
Приводится содержимое symb, постфиксной строки и opstk после просмотра каждого символа. Вершина opstkнаходится справа.
| Строка | symb | Постфиксная строка | opstk |
| A | A | ||
| + | A | + | |
| B | AB | + | |
| * | AB | +* | |
| C | ABC | +* | |
| ABC* | + | ||
| ABC*+ |
Строки 1, 3 и 5 соответствуют просмотру операнда таким образом, что символ (symb) немедленно помещается в постфиксную строку. В строке 2 была обнаружена операция, а стек оказался пустым, поэтому операция помещается в стек. В строке 4 приоритет нового символа (*) больше, чем приоритет символа, расположенного в вершине стека (+), поэтому новый символ помещается в стек. На 6-м и 7-м шагах входная строка пуста, поэтому из стека считываются элементы, которые затем помещаются в постфиксную строку.
Пример2:
| Строка | symb | Постфиксная строка | Opstk |
| ( | ( | ||
| A | A | ( | |
| + | A | (+ | |
| B | AB | (+ | |
| ) | AB+ | ||
| * | AB+ | * | |
| AB+C* |
В этом примере при обнаружении правой скобки из стека начинают извлекаться элементы до тех пор, пока не будет обнаружена левая скобка, после чего обе скобки отбрасываются. Использование скобок для изменения приоритетности выполнения операций приводит к последовательности их расположения в постфиксной строке, отличной от последовательности в примере 1.
Стек используется для запоминания в нем просмотренных ранее операций.
Если текущая просматриваемая операция имеет больший приоритет, чем операция, расположенная в вершине стека, то эта новая операция записывается в стек. Это означает, что при окончательной выборке из стека всех элементов и записи их в одну строку в постфиксной форме эта новая операция будет предшествовать операции, ранее расположенной перед ним (что является правильным, поскольку она имеет более высокий приоритет). С другой стороны, если приоритет новой операции меньший или равный, чем у операции из стека, то операция, находящаяся на вершине стека, должна быть выполнена первой. Следовательно, она извлекается из стека и помещается в выходную строку, а текущий рассматриваемый символ сравнивается со следующим элементом, занимающим теперь вершину стека, и т.
д. Помещая во входную строку скобки, можно изменить последовательность вычислений. Так, при обнаружении левой скобки она записывается в стек. При обнаружении соответствующей ей правой скобки все операции между этими скобками помещаются в выходную строку, поскольку они выполняются прежде любых других операций, расположенных за этими скобками.
Инфиксная нотация — это форма записи математических и логических формул, в которой операторы записаны в инфиксном стиле между операндами на которые они воздействуют (например 2 + 2). Задача разбора выражений записанных в такой форме для компьютера сложнее по сравнению с префиксной (то есть + 2 2) или постфиксной (2 2 +). Однако эта запись используется в большинстве языков программирования как более естественная для человека.
В инфиксной нотации, в отличие от префиксной и постфиксной, скобки, окружающие группы операндов и операторов, определяют порядок в котором будут выполнены операции. При отсутствии скобок операции выполняются согласно правилам приоритета операторов.
«Antananarivo» — перевод на русский
Инфиксная запись может отличаться от функциональной, где имя функции описывает какую-то операцию, а её аргументы являются операндами. Примером функциональной записи может быть S(1,3) в которой функция S означает операцию сложения: S(1,3) = 1+3 = 4.