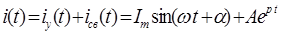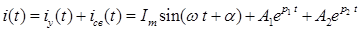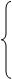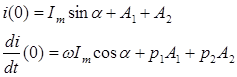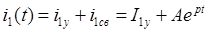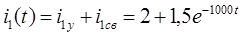Что такое постоянная интегрирования

25.10.202323.04.2022 admin 0 Comments

ПОСТОЯННАЯ ИНТЕГРИРОВАНИЯ

Смотреть что такое «ПОСТОЯННАЯ ИНТЕГРИРОВАНИЯ» в других словарях:

постоянная интегрирования — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN integration constant … Справочник технического переводчика

постоянная интегрирования — integravimo konstanta statusas T sritis fizika atitikmenys: angl. constant of integration vok. Integrationskonstante, f rus. константа интегрирования, f; постоянная интегрирования, f pranc. constante d’intégration, f … Fizikos terminų žodynas

постоянная интегрирования — integralinio poveikio koeficientas statusas T sritis automatika atitikmenys: angl. integral action coefficient vok. Integralwirkungsfaktor, m rus. коэффициент интегрирующего воздействия, m; постоянная интегрирования, f pranc. coefficient d action … Automatikos terminų žodynas

постоянная интегрирования — integravimo pastovioji statusas T sritis automatika atitikmenys: angl. constant of integration vok. Integrationskonstante, f rus. постоянная интегрирования, f pranc. constante d intégration, f … Automatikos terminų žodynas

константа интегрирования — integravimo konstanta statusas T sritis fizika atitikmenys: angl. constant of integration vok. Integrationskonstante, f rus. константа интегрирования, f; постоянная интегрирования, f pranc. constante d’intégration, f … Fizikos terminų žodynas

Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия

Исчисление — У этого термина существуют и другие значения, см. Исчисление (значения) … Википедия

Омический контакт — контакт между металлом и полупроводником или двумя полупроводниками, характеризующийся линейной симметричной вольт амперной характеристикой (ВАХ). Если ВАХ является асимметричной и нелинейной, контакт является не омическим а выпрямляющим,… … Википедия

Задача Кеплера в общей теории относительности — Общая теория относительности … Википедия

Integrationskonstante — integravimo konstanta statusas T sritis fizika atitikmenys: angl. constant of integration vok. Integrationskonstante, f rus. константа интегрирования, f; постоянная интегрирования, f pranc. constante d’intégration, f … Fizikos terminų žodynas

Источник

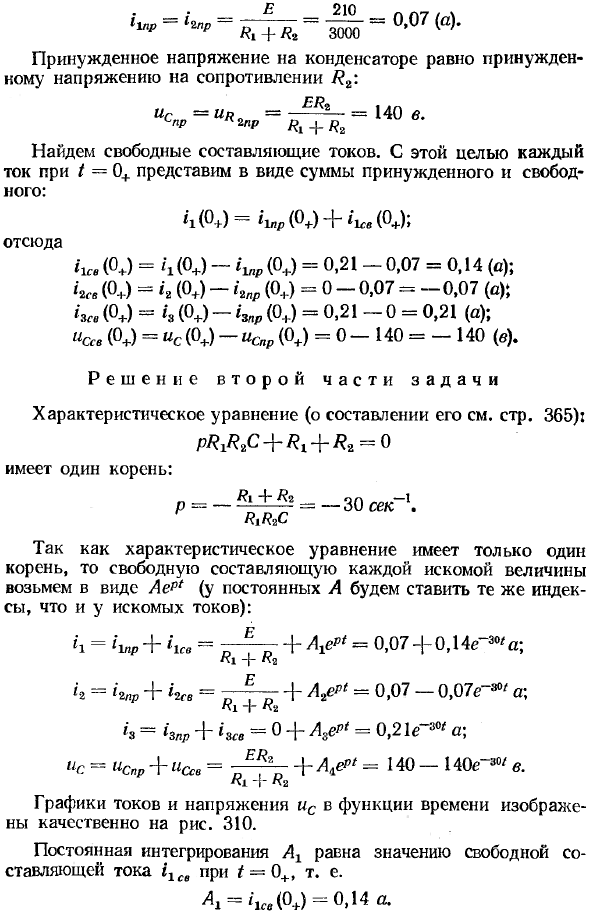
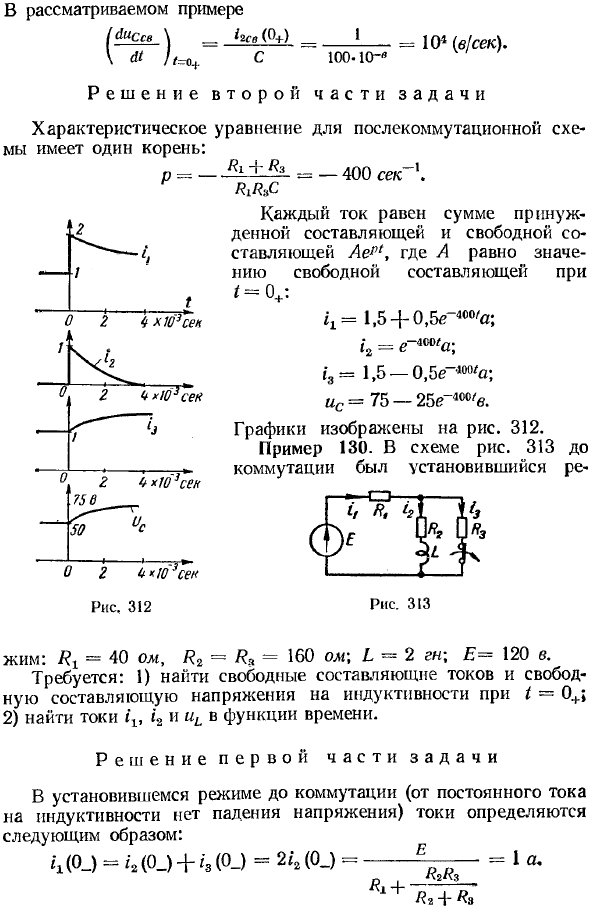
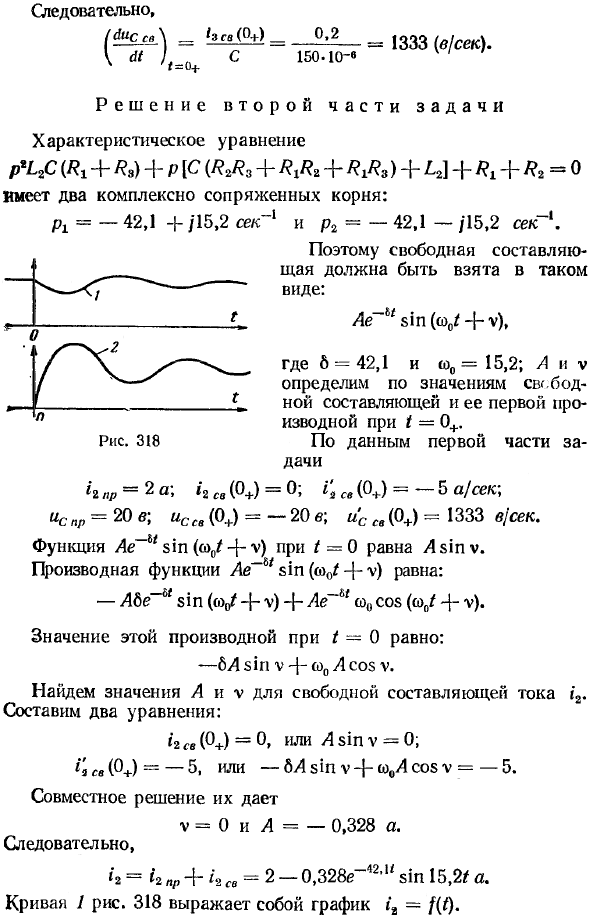
Определение постоянных интегрирования в классическом методе

Определение констант интегрирования классическим способом. Как известно из предыдущего, свободный ток или свободное напряжение могут быть выражены в виде суммы экспоненциальных членов. Количество полных слагаемых равно числу корней в характеристическом уравнении.

Значение первой производной тока обозначено как i’ce (0,.). Значение второй производной свободного тока при t = 0+ обозначено как & (0+) и т. Д. Подумайте, как определить интегральную константу A, …, Zce (0+), Людмила Фирмаль

Время Дифференцируем с уравнением (10.18), получим: ice — A6e

Найдите свободные составляющие тока, для этого каждый ток при t = 0+ является принудительным и свободным Может быть выражена как сумма: отсюда (0J = ((° +) ™ imp (0J = 0,21-0,07 = 0,14 (o);) == Е — ^ — и Ri + R *

Найти начальное значение производной 2) Определить ток t2, t3 и напряжение u как функцию времени Решение первой части задачи i2 (0_) = 0 и «1 (0_) = i, до переключения (0_) = = — = 1 (a) n H1 + H1 + H3 150 Вт конденсатора Соответствует ли напряжение напряжению резистора? 3: (0-) == H (0-) = 1 • 50 = 50 (c).

В этом примере / dt ^ Cce \ _ ^ 2Св (фу) 1 = 10 * (в! сек). \ # // m> + С100.1О

Таким образом, i = inp + ice = 35,2 sinˆ-20′) 8,54e

2 | 0 / a. Свободный ток, кривая 4 — общий ток после переключения (ордината кривой 4 при ω / 0 — кривая 2 и 5 Она равна сумме координат). Пример 132. На рисунке 317 замыкает переключатель на третьей ветви.

Отсутствует падение напряжения от постоянного тока на индуктивности, поскольку ток не течет в конденсатор, поэтому вынужденное напряжение на конденсаторе от 1Lpr до падения напряжения с резистора /? 2 от тока u = 2.10 = 20 (c)

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник

Определение постоянных интегрирования

Определение постоянных интегрирования производится на заключительном этапе расчета переходного процесса, когда остальные составляющие решения уже найдены. Постоянные интегрирования определяются путем подстановки в решение для искомой функции соответствующих начальных условий.

Пусть решение для искомой функции i(t) содержит только одну постоянную интегрирования:

Постоянная интегрирования находится путем подстановки в решение начального условия для самой функции, т.е. i(0):

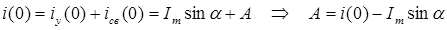
Пусть решение для искомой функции i(t) содержит две постоянных интегрирования и имеет вид:

Постоянные интегрирования в этом случае находятся путем подстановки в решение начальных условий для самой функции i(0) и для ее первой производной :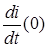

Последовательность выполнения отдельных этапов расчета переходных процессов классическим методом показана ниже в виде диаграммы.

Что такое постоянная интегрирования. Смотреть фото Что такое постоянная интегрирования. Смотреть картинку Что такое постоянная интегрирования. Картинка про Что такое постоянная интегрирования. Фото Что такое постоянная интегрирования

Примечания:1. Выполнение всех этапов, обозначенных в диаграмме клетками, является обязательным и необходимым.

2. Выполнение первых пяти этапов, находящихся в верхнем горизонтальном ряду диаграммы, может производиться в любой последовательности, так как они не зависят друг от друга.

Пример. Для схемы рис. 132 с заданными параметрами элементов: Е=100 В, R=50 Ом, R₁=20 Ом, R₂=30 Ом, С=83,5 мкФ, определить ток i₁ после коммутации.

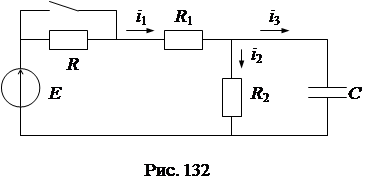1)Общий вид решения для искомой функции:

2)Определение установившейся составляющей израсчета схемы после коммутации:

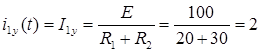
3)Характеристическое уравнение и его корень:

4)Независимое начальное условие u_с(0) из расчета схемы до коммутации:

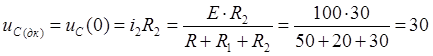
5)Система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации:

(1)

(2)

(3)

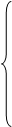
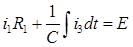
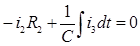
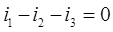
6)Начальное условие i₁(0), необходимое для определения постоянной интегрирования из уравнения (1):

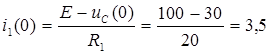
7)Определение постоянной интегрирования:

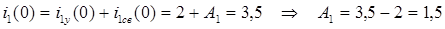
8)Решение для искомой функции:

9)Графическая диаграмма искомой функции i₁(t) показана на рис. 133:

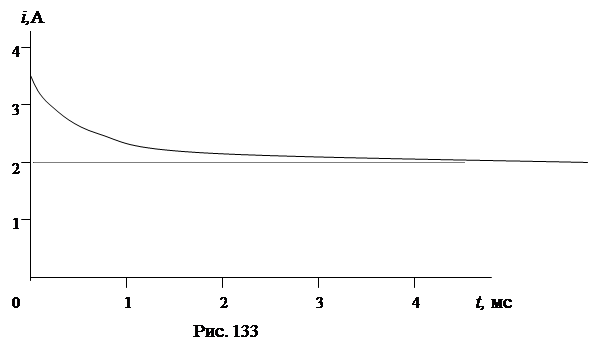9. Операторный метод расчета переходных процессов

Если система дифференциальных уравнений, которыми описывается переходной процесс в схеме, решается операционным методом, то и сам метод расчета переходного процесса также называется операционным или операторным.

Сущность операторного метода состоит в том, что на 1-ом этапе действительные функции времени i(t), u(t), называемые оригиналами, заменяются некоторыми новыми функциями I(p),U(p), называемыми операторными изображениями. Соответствие между оригиналом функции f(t) и ее операторным изображением F(p) устанавливается на основе прямого преобразования интеграла Лапласа:

или ,

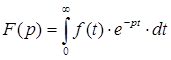
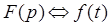
Если s = 0, то p= jw, и преобразование Лапласа превращается в преобразование Фурье, которое лежит в основе комплексного метода расчета цепей переменного тока.

Преобразование Лапласа позволяет заменить операции 2-го рода над оригиналами функций (дифференцирование и интегрирование) на операции 1-го рода (умножение и деление) над операторными изображениями этих функций.

Расчет переходных процессов операторным методом условно выполняется в 3 этапа.

На 1-м этапе расчета система дифференциальных уравнений, составленная по законам Кирхгофа для оригиналов функций, после применения преобразования Лапласа превращается в систему алгебраических уравнений для операторных изображений этих функций.

На 2-ом этапе выполняется решение системы алгебраических операторных уравнений относительно искомой функции, в результате чего получают выражение искомой функции в операторной форме F(p).

На заключительном 3-м этапе выполняется обратный переход от найденного операторного решения для искомой функции F(p) к соответствующей ей функции времени f(t), т. е. Выполняется переход от изображения функции F(p)к ее оригиналу f(t).

Теоретически обратный переход от операторного изображения функции F(p)к ее оригиналу f(t) устанавливается на основе обратного преобразования Лапласа:

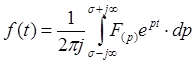
На практике для обратного перехода используются более простые и удобные методы, а именно: формула разложения и таблицы соответствия.

Источник

Константа интеграции: значение, расчет и примеры

Содержание:

В постоянная интеграции Это дополнительная ценность для вычисления первообразных или интегралов, она служит для представления решений, составляющих примитив функции. Он выражает внутреннюю неоднозначность, когда любая функция имеет бесконечное количество примитивов.

Например, если мы возьмем функцию: f (x) = 2x + 1 и получим ее первообразную:

∫ (2x + 1) dx = х 2 + х + C ; куда C это постоянная интеграции и графически представляет вертикальный переход между бесконечными возможностями примитива. Правильно сказать, что (x 2 + x) есть а примитивов f (x).

Таким же образом вы можете определить (x 2 + х + C ) как примитив f (x).

Обратное свойство

Можно отметить, что при выводе выражения (x 2 + x), мы получаем функцию f (x) = 2x + 1. Это связано с обратным свойством, существующим между выводом и интегрированием функций. Это свойство позволяет получать формулы интегрирования, начиная с дифференцирования. Это позволяет проверять интегралы через те же производные.

Где 1, 2, 3 и 4 представляют конкретные примитивы f (x) = 2x + 1. В то время как 5 представляет неопределенный или примитивный интеграл f (x) = 2x + 1.

Примитивы функции получаются посредством первичного или интегрального процесса. Где F будет примитивом f, если верно следующее

Можно видеть, что функция имеет единственную производную, в отличие от ее бесконечных примитивов, полученных в результате интегрирования.

Неопределенный интеграл

Он соответствует семейству кривых с одинаковым рисунком, которые испытывают несоответствие в значениях изображений каждой точки (x, y). Каждая функция, отвечающая этому шаблону, будет отдельным примитивом, а набор всех функций известен как неопределенный интеграл.

Ценность постоянная интеграции именно он отличает каждую функцию на практике.

В постоянная интеграции предлагает вертикальный сдвиг на всех графиках, которые представляют примитивы функции. Где наблюдается параллелизм между ними, и то, что C это значение смещения.

Согласно общепринятой практике постоянная интеграции он обозначается буквой «C» после добавления, хотя на практике не имеет значения, добавляется или вычитается константа. Его реальную ценность можно найти разными способами в зависимости от первоначальные условия.

Другие значения постоянной интеграции

Уже говорилось о том, как постоянная интеграции применяется в отрасли интегральное исчисление; Представление семейства кривых, определяющих неопределенный интеграл. Но многие другие науки и отрасли приписывают очень интересные и практические ценности постоянная интегрирования, которые способствовали развитию множества исследований.

В постоянная интеграции он будет представлять значение начальной позиции, то есть в момент t = 0.

Аналогично, если функция известна В) который представляет собой ускорение частицы против времени. Примитив A (t) приведет к функции V (t), где постоянная интеграции будет значением начальной скорости V₀.

в экономия, получая посредством интегрирования примитив функции стоимости. В постоянная интеграции будут представлять собой постоянные затраты. И так много других приложений, заслуживающих дифференциального и интегрального исчисления.

Как рассчитывается постоянная интегрирования?

Для расчета постоянная интегрирования, всегда будет необходимо знать первоначальные условия. Которые отвечают за определение того, какой из возможных примитивов является соответствующим.

Во многих приложениях он рассматривается как независимая переменная в момент времени (t), где постоянная C принимает значения, которые определяют первоначальные условия конкретного случая.

Если взять исходный пример: ∫ (2x + 1) dx = x 2 + х + C

Допустимое начальное условие может заключаться в том, что график проходит через определенную координату. Например, известно, что примитив (x 2 + х + C) проходит через точку (1, 2)

F (х) = х 2 + х + C; это общее решение

Подставим в это равенство общее решение

Отсюда легко следует, что C = 0

Таким образом, соответствующий примитив для этого случая есть F (х) = х 2 + х

Есть несколько типов числовых упражнений, которые работают с константы интегрирования. Фактически, дифференциальное и интегральное исчисление не перестают применяться в современных исследованиях. Их можно найти на разных академических уровнях; от первоначального расчета, через физику, химию, биологию, экономику и другие.

Это также видно при изучении дифференциальные уравнения, где постоянная интеграции Он может принимать разные значения и решения, это связано с многочисленными производными и интеграциями, которые выполняются в этом вопросе.

Примеры

Пример 1

Известно, что при прямолинейном движении, равномерно изменяющемся, ускорение является постоянной величиной. Это случай запуска снаряда, где ускорение будет равным гравитации.

Начальные условия упражнения указывают на то, что начальная скорость равна V₀ = 25 м / с. Это скорость в момент времени t = 0. Таким образом выполняется следующее:

С определенной функцией скорости

Аналогичным образом мы продолжаем интегрировать функцию скорости, чтобы получить выражение, определяющее положение:

Начальное положение R (0) = 30 м известно. Затем вычисляется конкретный примитив снаряда.

Поскольку это заставляет частицу достигнуть земли (позиция = 0)

Таким образом решается второй участок, где время полета равно 6 секундам.

Пример 2

Когда информация о второй производной f ’’ (x) = 4, начинается процесс антидеривации.

Затем, зная условие f ‘(2) = 2, переходим:

Проделайте то же самое для второго постоянная интеграции

Начальное условие f (0) = 7 известно и приступаем:

Аналогично предыдущей задаче мы определяем первые производные и исходную функцию из начальных условий.

∫ (х 2 ) dx = (x 3 / 3) + С₁

При условии f ‘(0) = 6 переходим:

( 0 3 / 3) + С₁ = 6; куда₁ = 6 и f ’(x) = (x 3 /3 ) + 6

Затем второй постоянная интеграции

∫ [(x 3 / 3) + 6] dx = (x 4 / 12) + 6x + С₂

Начальное условие f (0) = 3 известно и приступаем:

[(0) 4 / 12] + 6 (0) + C₂ = 3; куда₂ = 3

Таким образом, мы получаем примитивное частное

f (x) = (Икс 4 / 12) + 6x + 3

Пример 3

Важно помнить, что производные относятся к наклону линии, касательной к кривой в данной точке. Где некорректно предполагать, что график производной касается указанной точки, поскольку она принадлежит графику примитивной функции.

Таким образом, мы выражаем дифференциальное уравнение следующим образом:

Применение начального условия:

Выразим дифференциальное уравнение следующим образом:

Применение начального условия:

Предлагаемые упражнения

Упражнение 1

Упражнение 2.

Упражнение 3.

Упражнение 4.

Ссылки

Синдром Рамзи Ханта: причины, симптомы и лечение

Источник

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

Отличительными особенностями её являются:

использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

В случае с вещественными числами.

Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).

Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение

Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).

Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .