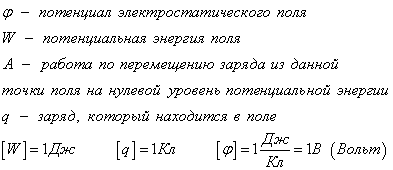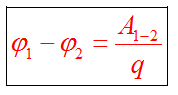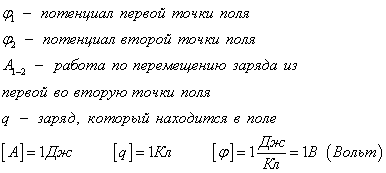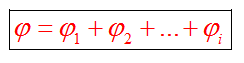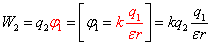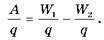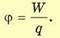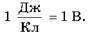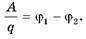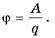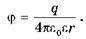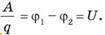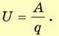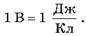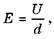Что такое потенциалы в физике

ПОТЕНЦИАЛ

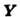
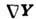
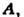
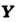
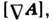
Если векторное поле соленоидально, т. е.= О, то для этого поля можно ввести векторный потенциал такой, что =при этомопределён с точностью до градиента произвольной ф-ции ( градиентная инвариантность). В общем случае любое векторное поле представляется суммой потенциального и соле-ноидального полей.

Лит.: Тамм И. П., Основы теории электричества, 10 изд., М., 1989; Ландау Л. Д., Лифшиц E. М., Теория поля, 7 изд., М., 1988; Славное А. А., Фаддеев Л. Д., Введение в квантовую теорию калибровочных полей, 2 изд., М., 1988. Л. О. Чехов.

Полезное

Смотреть что такое «ПОТЕНЦИАЛ» в других словарях:

ПОТЕНЦИАЛ — ПОТЕНЦИАЛ. Количество любого вида энергии может быть выражено произведением двух различных величин, из к рых одна характеризует «уровень энергии», определяет направле ние, в к ром должен совершаться ее переход; так напр. тяжелое тело… … Большая медицинская энциклопедия

потенциал — ресурсы, заряд, резерв, запас, (внутренние, жизненные) резервы, возможности, биопотенциал Словарь русских синонимов. потенциал см. возможности Словарь синонимов русского языка. Практический справочник. М.: Русский язык … Словарь синонимов

ПОТЕНЦИАЛ — (физ.) в учении об электричестве так называется величина электрического состояния на поверхности проводника, имеющая большое сходство с тем, что в учении о теплоте называется температурою, и измеряющая напряжение электрич. на проводниках. Словарь … Словарь иностранных слов русского языка

потенциал — электрический потенциал данной точки Разность электрических потенциалов данной точки и другой определенной, произвольно выбранной точки. [ГОСТ Р 52002 2003] потенциал Общий термин, означающий предельную возможность или способность какой то… … Справочник технического переводчика

ПОТЕНЦИАЛ — ПОТЕНЦИАЛ, потенциала, муж. (от лат. potentia сила, возможность). 1. Физическое понятие, характеризующее величину потенциальной энергии в определенной точке пространства (физ., тех.). Потенциал силы притяжения. Разность потенциалов. 2. перен.… … Толковый словарь Ушакова

ПОТЕНЦИАЛ — (от латинского potentia сила), источники, возможности, средства, запасы, которые могут быть использованы для решения какой либо задачи, достижения определенной цели; возможности отдельного лица, общества, государства в определенной области… … Современная энциклопедия

ПОТЕНЦИАЛ — (потенциальная функция) понятие, характеризующее широкий класс физических силовых полей (электрических, гравитационных и т. п.) и вообще поля физических величин, представляемых векторами (поле скоростей жидкости и т. п.). В общем случае потенциал … Большой Энциклопедический словарь

ПОТЕНЦИАЛ — (от лат. potentia сила) источники, возможности, средства, запасы, которые могут быть использованы для решения какой либо задачи, достижения определенной цели; возможности отдельного лица, общества, государства в определенной области (напр.,… … Большой Энциклопедический словарь

потенциал — 1. В физике величина, характеризующая в данной точке силовое поле электрическое, магнитное, гравитационное и пр. Соответственно различаются потенциал электрический, магнитный и пр. 2. Совокупность наличных средств, возможностей в некоей области,… … Большая психологическая энциклопедия

Источник

Учебники

Журнал «Квант»

Общие

Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

Если W_p2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

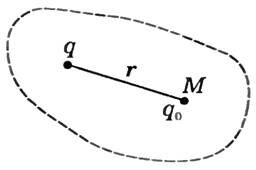
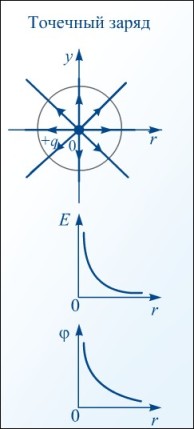
Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 2).

Будем помещать в точку Μ этого поля различные пробные положительные заряды q₀. Потенциальная энергия их различна, но отношение \(

\frac = \operatorname\) для данной точки поля и служит характеристикой поля, называемой потенциалом поля φ в данной точке:

Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).

Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.

Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.

Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.

Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.

В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда q₀ становится определенной величиной.

На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой

При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:

если q > 0, то φ > 0; если q

По этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.

Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q₀ помещенного в эту точку: W_p1 = q₀φ. Если положить, что W_p2 = 0, то из уравнения (1) будем иметь

Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q₀ из данной точки в нулевую. Из последней формулы имеем

Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).

Потенциальная энергия заряда q₀ помещенного в электростатическое поле точечного заряда q на расстоянии r от него,

Если q и q₀ — одноименные заряды, то W_p > 0, если q и q₀ — разные по знаку заряды, то W_p \(

где φ_i — потенциал поля, созданного всеми зарядами, кроме заряда q_i, в той точке поля, где находится заряд q_i.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 229-231.

Источник

III. Основы электродинамики

Тестирование онлайн

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде

Напряжение

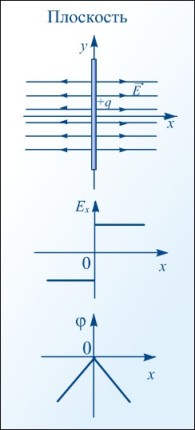
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

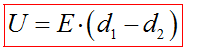
От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Как определить знак потенциала

При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.

На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу 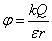подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.

Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.

Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.

Зависимость напряженности и потенциала от расстояния

Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен

Напряжение в природе

Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Энергия взаимодействия зарядов*

Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q₁ и q₂, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q₂ из бесконечности в данную точку поля, созданного зарядом q₁

Аналогично Тогда энергия взаимодействия двух точечных зарядов

Источник

Учебники

Журнал «Квант»

Общие

Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

Если W_p2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 2).

Будем помещать в точку Μ этого поля различные пробные положительные заряды q₀. Потенциальная энергия их различна, но отношение \(

\frac = \operatorname\) для данной точки поля и служит характеристикой поля, называемой потенциалом поля φ в данной точке:

Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).

Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.

Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.

Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.

Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.

В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда q₀ становится определенной величиной.

На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой

При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:

если q > 0, то φ > 0; если q

По этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.

Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q₀ помещенного в эту точку: W_p1 = q₀φ. Если положить, что W_p2 = 0, то из уравнения (1) будем иметь

Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q₀ из данной точки в нулевую. Из последней формулы имеем

Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).

Потенциальная энергия заряда q₀ помещенного в электростатическое поле точечного заряда q на расстоянии r от него,

Если q и q₀ — одноименные заряды, то W_p > 0, если q и q₀ — разные по знаку заряды, то W_p \(

где φ_i — потенциал поля, созданного всеми зарядами, кроме заряда q_i, в той точке поля, где находится заряд q_i.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 229-231.

Источник

Потенциал электрического поля

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W₁ — W₂ на заряд q, получим

Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

Единица потенциала — вольт:

Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ_∞ ). Поскольку φ_∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

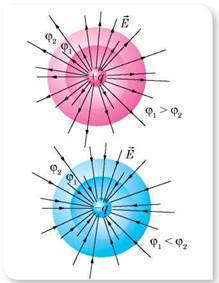
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

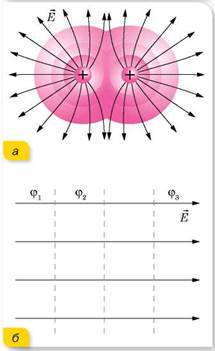
Разность потенциалов

Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,

Единица разности потенциалов (напряжения), как и потенциала, — вольт,

Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ₁ и φ₂ ) выполненная полем работа не зависит от траектории этого движения.

Связь напряженности электрического поля с напряжением

Из формул A = Eqd и A = qU можно установить связь между напряженностью и напряжением электрического поля: Ed = U. С этой формулы следует:

то именно из этой формулы и выводится еще одна единица напряженности — вольт на метр,

Источник