Что такое потеря полволны и когда она наблюдается

Потеря половины длины волны

нагуглил ответ на свой последний вопрос тут
http://www.physbook.ru/ind…

цитата оттуда:
«При отражении луча от среды с меньшим показателем преломления фаза колебаний волны не меняется. При отражении луча от среды с большим показателем преломления, волна меняет фазу колебаний на противоположную (на π), что равносильно потере полуволны (λ/2). «

В соответствии с формулами Френеля на границе раздела двух сред преломленная световая волна всегда в фазе с падающей волной, отраженная волна — либо в фазе, либо в противофазе.

Иной сдвиг фазы отраженной волны возникает только в случае полного внутреннего отражения.

Проанализируйте формулы Френеля, анализ даст ответ на Ваш вопрос))

Задайте свой вопрос по физике
профессионалам

Другие вопросы на эту тему:

Задача по оптике

луч света падает на границу раздела двух сред под углом 32 градуса абсолютный показатель преломления первой среды равен 2,4. каков абсолютный показатель преломления второй среды если известно что преломленный луч перпендикулярен отраженному?

если можно с решением

Толщина пленки

Помогите пожалуйста с задачкой по оптике

Интерференция света

Задача:
«Лучи белого света падают под углом alpha = 60гр на очень тонкую прозрачную пластинку. При этом пластинка в отраженном свете кажется зеленой. Как изменится цвет пластинки, при небольшом уменьшении угла падения лучей? При его увеличение?»

решение:
http://s1.ipicture.ru/uploa….png
честно говоря я уже совсем запарился — не могу себе…

Помогите решить 2 задачи по физике

1) На стеклянную пластинку положена выпуклой сторой плоско-выпуклая линза. Сверхулинза освещена монохроматически светом длиной волны 5*10^-7 м. Найти радиус кривизны линзы, если радиус четвертого тёмного кольца Ньютона в отраженном свете равен 2 мм.

2)На поверхность дифракционной решетки нормально падает монохроматический свет. постоянная дифракционной решетки в 4,6 раза больше длины световой волны. Найти общее число дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.

Источник

Что такое потеря полволны и когда она наблюдается

Пусть световая волна распространяется в направлении оси Z. Тогда вектор лежит в плоскости XY, так как перпендикулярен направлению распространения. Если вектор колеблется вдоль какой-то линии в этой плоскости, то световая волна называется линейно поляризованной. Если вектор произвольно меняется в плоскости XY, то в каждый момент времени его можно разложить на сумму двух векторов вдоль осей X и Y. Произвольную волну, распространяющуюся вдоль оси Z, можно представить, как сумму двух линейно поляризованных волн с колебанием вектора вдоль осей X и Y соответственно.

Если конец вектора вращается по окружности в плоскости XY, то такой свет называется циркулярно поляризованным или светом с круговой поляризацией. Свет поляризован по левому кругу, если в фиксированной точке при наблюдении навстречу свету вектор (как и вектор ) вращается по левому кругу, то есть против часовой стрелки. Если конец вектора описывает эллипс, то волна называется эллиптически поляризованной. Если волна монохроматическая, то конец вектора описывает эллипс, окружность, либо вектор гармонически колеблется вдоль линии.

При сложении двух или нескольких световых волн складываются не интенсивности волн, а напряженности и световых полей. При этом если интенсивность суммы полей отличается от суммы интенсивностей, то говорят, что эти световые поля интерферируют. Если световые поля способны интерферировать, то их называют когерентными друг другу.

Если на пути распространения световой волны встречается препятствие, то волна его огибает, поворачивает «за угол». Это явление называется дифракцией. Препятствием, например, может быть любой объект, который не пропускает, «загораживает», часть фронта световой волны.

V. ИНТЕРФЕРЕНЦИЯ.

Явление интерференции состоит в том, что при сложении двух или нескольких световых волн, суммарная интенсивность света отличается от суммы интенсивностей. Это возможно потому, что складываются напряженности и световых волн, а интенсивность суммы световых волн можно найти, в соответствии с определением интенсивности, по формуле (в системе единиц СГС Гаусса).

Интерференцию света обычно рассматривают не в одной точке, а на плоском экране. Поэтому говорят об интерференционной картине, под которой понимают чередующиеся полосы относительно большей и меньшей интенсивности света. Основными характеристиками интерференционной картины являются ширина полос интерференции и видность интерференционной картины.

Волны с ортогональными линейными поляризациями не интерферируют, так как для них интенсивность суммарной волны всегда равна сумме интенсивностей исходных волн. В том же смысле ортогональны лево и право циркулярно поляризованные волны.

Поляризатор.

Плоскопараллельную фазовую пластинку или изготавливают из одноосного кристалла, так что направление оси кристалла лежит в плоскости пластинки. Свет, падающий перпендикулярно на фазовую пластинку, распространяется в ней в виде двух независимых световых волн линейно поляризованных во взаимно перпендикулярных направлениях. Поляризация (направление вектора ) обыкновенной волны перпендикулярна оси кристалла. Поляризация необыкновенной волны совпадает с направлением оси кристалла.

Пластинка интересна тем, что она позволяет получить циркулярно поляризованный свет из линейно поляризованного и наоборот. Чтобы получить циркулярно поляризованный свет из линейно поляризованного, направление линейной поляризации на входе пластинки должно составлять угол с направлением оси кристалла (свет падает перпендикулярно пластинке). Только в этом случае амплитуды обыкновенной и необыкновенной волн в кристалле равны.

Двухлучевая интерференция.

Под двухлучевой интерференцией понимают интерференционную картину, возникающую при сложении двух световых волн одинаковой частоты.

При сложении двух волн одинаковой поляризации с интенсивностями и интенсивность суммарной волны получаем аналогично:

Оптическая разность хода.

Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле:

Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:

Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.

Ширина интерференционных полос.

Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.

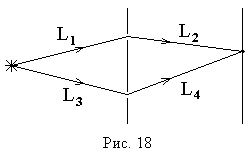
где знак ‘+’ соответствует положительным углам падения и отсчитанным в разные стороны от нормали к экрану, как на рис. 19.

В большинстве задач углы падения малы, тогда и выражение для ширины полос упрощается

Потеря полуволны.

Интерференция и закон сохранения энергии.

Совместим с помощью полупрозрачной пластинки две плоские световые волны одинаковой амплитуды, как показано на рис. 20. Тогда по формуле

Можно совмещать световые волны другим способом, как это изображено на рис. 23. Этот метод наблюдения интерференции называют методом деления волнового фронта.

Чтобы разобраться с этим вариантом парадокса необходимо учесть дифракцию волн. Попробуйте вернуться к его рассмотрению самостоятельно после изучения темы «Дифракция».

Источник

В тонких пластинках (пленках). Просветление оптики

Образование когерентных волн и интерференция происходят также при попадании света на тонкую прозрачную пластинку или пленку.

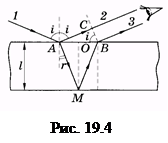
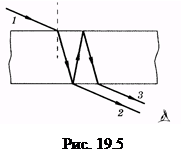
Пучок света падает на плоскопараллельную пластинку (рис. 19.4). Луч 1 из этого пучка попадает в точку А, частично отражается (луч 2), частично преломляется (луч AM). Преломленный луч испытывает отражение на нижней границе пластинки в точке М. Отраженный луч, преломившись в точке В, выходит в первую среду (луч 3). Лучи 2 и 3 образованы от одного луча, поэтому они когерентны и будут интерферировать.

Найдем оптическую разность хода лучей 2 и 3. Для этого из точки В проведем нормаль ВС к лучам. От прямой ВС до встречи лучей их оптическая разность хода не изменится, линза или глаз не внесут дополнительной разности фаз. До расхождения в точке А эти лучи в совокупности с другими, параллельными им, не показанными на рис. 19.4, формировали луч 1 и поэтому, естественно, имели одинаковую фазу. Луч 3 прошел расстояние ÷АМ÷ + ÷МВ÷ в пластинке с показателем преломления п, луч 2 — расстояние ÷АС÷в воздухе, поэтому их оптическая разность хода

так как ÷АМ÷ =÷МВ÷. Согласно закону преломления,

п = sin i/sin r или sin i = n sin r, (19.13)

где i— угол падения, r — угол преломления.

Из DАМО находим: ÷АМ÷ =÷OM÷/cos r = l/cos r, ÷АО÷ =÷ ОМ÷ tgr = I tg r (l— толщина пластинки). Из DАСВ находим |АС| = |AB| sin i = 2|АО| ´ sin i. Учитывая эти равенства, а также (19.13), получаем
|АС| =2lntg r sin r = 2ln sin 2 r/cos r.

Тогда оптическая разность хода интерферирующих волн равна

В формуле (19.14) не учтено одно важное обстоятельство. Опыт показывает, что при отражении света от среды оптически более плотной, т. е. с большим показателем преломления, фаза волны изменяется на p, что соответствует [см. (19.9)] изменению оптической разности хода на l/2, т. е. при отражении света от среды оптически более плотной происходит «потеря полволны».

Если бы оба луча 2 и 3 теряли полволны, то это не изменило бы выражения для 8 (19.14). Однако луч 2 отражается от среды оптически более плотной (точка А) и теряет полволны, а луч 3 отражается от среды оптически менее плотной (точка М), его фаза при этом не изменяется.
С учетом потери полволны оптическая разность хода

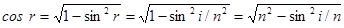
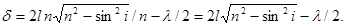
Так как ,то d можно выразить и через угол падения:

(19.16)

Для максимума интерференции [см. (19.10), (19.16)] имеем

Для минимума интерференции [см. (19.11), (19.16)] имеем

Формулы (19.17) и (19.18) соответствуют интерференции в отраженном свете. Интерференция в проходящем через пластинку свете показана на рис. 19.5; изображены только те лучи, которые необходимы для понимания явления.

Читатель может самостоятельно вывести соответствующие формулы и убедиться, что для этого случая (19.17) соответствует минимуму интерференции, а (19.18) — максимуму. С учетом закона сохранения энергии это понятно, так как интерференция есть перераспределение световой энергии: падающий поток перераспределяется пластинкой на отраженный и проходящий (поглощением здесь пре­небрегаем), причем если отраженный максимален, то проходящий минимален, и наоборот.

Интерференция при отражении наблюдается более отчетливо, чем в проходящем свете, что обусловлено существенным различием интенсивностей отраженного и проходящего лучей. Если принять, что на границе раздела прозрачных сред отражается около 5% падающей энергии, то

где I₁ и I₂ — интенсивности лучей 1 и 2 соответственно (см. рис. 19.4). Интенсивность луча 3 с учетом двукратного преломления и однократного отражения равна

Из (19.19) и (19.20) имеем

что означает приближенное равенство амплитуд интерферирующих лучей при отражении: условие минимума соответствует почти полной темноте. Делая аналогичный расчет для проходящего света (рис. 19.5), получаем

Из (19.22) видно, что в проходящем свете интерферируют волны с существенно различными амплитудами, поэтому максимумы и минимумы мало отличаются друг от друга и интерференция слабо заметна.

Проанализируем зависимости (19.17) и (19.18).

Если на тонкую плоскопараллельную пластинку под некоторым углом падает параллельный пучок монохроматического излучения, то, согласно этим формулам, пластинка в отраженном свете выглядит яркой или темной.

При освещении пластинки белым светом условия максимума и минимума выполняются для отдельных длин волн, пластинка станет окрашенной, причем цвета в отраженном и проходящем свете будут дополнять друг друга до белого.

При падении монохроматического света на пластинку переменной толщины каждому значению l соответствует свое условие интерференции, поэтому пластинка пересечена светлыми и темными линиями (полосами) — линиями равной толщины. Так, в клине это сиcтема параллельных линий (рис. 19.6), в воздушном промежутке между линзой и пластинкой — кольца (кольца Ньютона).

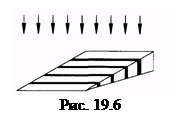
При освещении пластинки переменной толщины белым светом получаются разноцветные пятна и линии: окрашенные мыльные пленки, пленки нефти и масла на поверхности воды, переливчатые цвета крыльев некоторых насекомых и птиц. В этих случаях не обязательна полная прозрачность пленок.

Особый практический интерес имеет интерференция в тонких пленках в связи с созданием устройств, уменьшающих долю световой энергии, отраженной оптическими системами, и увеличивающих, следовательно, энергию, поступающую к регистрирующим системам — фотопластинке, глазу и т. п. С этой целью поверхности оптических систем покрывают тонким слоем оксидов металлов так, чтобы для некоторой средней для данной области спектра длины волны был минимум интерференции в отраженном свете. В результате возрастает доля прошедшего света. Покрытие оптических поверхностей специальными пленками называют просветлением оптики, а сами оптические изделия с такими покрытиями — просветленной оптикой.

Если на стеклянную поверхность нанести ряд специально подобранных слоев, то можно создать отражательный светофильтр, который вследствие интерференции будет пропускать или отражать излучение в определенном интервале длин волн.

Источник

Методичка к семинарам. Методические указания к практическим занятиям по курсу общей физики. Оптик а

Потеря полуволны
В соответствии с формулами Френеля [2, 3] на границе раздела двух сред преломленная световая волна всегда в фазе с падающей волной, отраженная волна — либо в фазе, либо в противофазе. Иной сдвиг фазы отраженной волны возникает только в случае полного внутреннего отражения.

При нормальном падении света на границу раздела двух сред отраженная волна в точке падения будет в противофазе с падающей при отражении от оптически более плотной среды, от среды с более высоким показателем преломления. Противоположная фаза отраженной волны эквивалентна сдвигу фазы на , или изменению разности хода на /2. Поэтому говорят, что при отражении от оптически более плотной среды происходит потеря полуволны. При этом в выражении для оптической длины пути следует добавить (или вычесть) слагаемое /2.

Если одна из интерферирующих волн по пути к экрану испытала отражение с потерей полуволны, как, например, при наблюдении колец Ньютона в отраженном свете, то без учета потери полуволны в рассчитанной интерференционной картине темные полосы окажутся на месте светлых, а светлые — на месте темных.
Интерференция и закон сохранения энергии
Совместим с помощью полупрозрачной пластинки две плоские световые волны одинаковой амплитуды, как показано на рис. 19. Тогда по формуле
I = 2I₀(1+cos(₁₂))
можно найти интенсивность суммарной волны. Если косинус в этом выражении равен (1), то I = 0. Куда же в таком случае делась энергия суммируемых волн? А если косинус равен (+1), то I=4I₀, что вдвое больше суммы интенсивностей суммируемых волн. Нет ли здесь противоречия с законом сохранения энергии?

В действительности противоречия нет, так как кроме сложения световых волн в направлении 1 (рис. 20) происходит сложение волн в направлении 2. И при изменении величины косинуса в приведенной выше формуле происходит перераспределение энергии между световыми волнами, идущими в этих направлениях.

Для обоих направлений косинус будет принимать одно и то же значение, и, если больше света идет в направлении 1, то, казалось бы, больше и в направлении 2. Противоречие с законом сохранения энергии остается?

Рис. 19

Рис. 20

Рис. 21
Положение спасает потеря полуволны. Для плоскопараллельной полупрозрачной пластинки это не так очевидно из–за многократных отражений. Задача становится более простой в случае, изображенном на рис. 21. Здесь полупространство вправо и вниз заполнено средой с показателем преломления n, а совмещение световых волн происходит при отражении и преломлении света на границе среда–вакуум. Если в направлении 1 отражение происходит с потерей полуволны, то в направлении 2 — без потери полуволны. Следовательно, увеличение света в направлении 1 сопровождается уменьшением интенсивности света в направлении 2. Таким образом, учет потери полуволны устраняет противоречие. Данный способ совмещения световых волн (в направлении 1 или в направлении 2) называется способом деления амплитуды.

Можно совмещать световые волны другим способом, как это изображено на рис. 22. Этот метод наблюдения интерференции называют методом деления волнового фронта.

Рис. 22
В методе деления волнового фронта интерферирующие волны неизбежно складываются под некоторым углом , что приводит к появлению интерференционных полос. Энергия световой волны при этом не возникает и не пропадает, она перераспределяется между светлыми и темными интерференционными полосами.

Частично когерентный свет

Световые волны когерентны, если они способны интерферировать. Оказывается, реальная световая волна не вполне когерентна сама себе. Две световые волны, полученные из одной методом деления амплитуды или методом деления волнового фронта, не обязательно интерферируют друг с другом. Есть две основные причины возможной некогерентности таких волн.
Первая причина — немонохроматичность источника света. Монохроматичный свет — свет одной частоты. Строго монохроматичная волна в каждой точке пространства имеет не зависящую от времени амплитуду и фазу. Как амплитуда, так и фаза реальной световой волны испытывают некоторые случайные изменения во времени или, как говорят физики, «шумят». Шумы фазы можно рассматривать как шумы частоты. Если шумы частоты невелики и шумы амплитуды достаточно медленные (их частота мала по сравнению с оптической частотой ), то говорят, что волна квазимонохроматическая.

Можно дать и другое, более удобное с математической точки зрения, определение квазимонохроматической волны. Любую волну можно представить как суперпозицию монохроматических плоских волн (Фурьеразложение по частотам и волновым векторам). Квазимонохроматическая волна имеет узкий спектр частот. Частоты составляющих ее волн находятся в узком диапазоне , таком, что  Квазимонохроматический свет
Квазимонохроматический свет можно представить как суперпозицию монохроматических волн, частоты которых расположены в узком спектральном диапазоне.

При сложении двух волн с различающимися частотами интенсивность суммарного света равна сумме интенсивностей суммируемых волн, и в этом смысле волны разных частот не интерферируют друг с другом, если время усреднения в выражении для интенсивности I = (c/4) 2 > устремить к бесконечности. При малом времени усреднения окажется, что волны разных частот интерферируют, но интерференционные полосы «бегут» по экрану, так что интенсивность света в каждой точке экрана гармонически осциллирует с частотой, равной разности частот суммируемых волн. Такую интерференционную картину можно наблюдать при сложении излучения двух однотипных лазеров.

Если в задаче специально не оговорено время усреднения, то подразумевается, что оно бесконечно. В таком случае интенсивность в каждой точке экрана представляет собой сумму интенсивностей интерференционных картин монохроматических световых волн, составляющих квазимонохроматический свет. Правильный результат при решении задачи получится и в том случае, если считать, что частота света медленно «гуляет» в пределах ширины спектральной линии излучения, а интерференционная картина при этом «смазывается», так как положение полос меняется в зависимости от частоты света.

Пусть частота излучения медленно изменяется от одного до другого края спектральной линии излучения на ширину спектральной линии . Если некоторая интерференционная полоса сдвигается при этом на расстояние, превышающее ширину полос, то через выбранную точку экрана «пробегает» то минимум, то максимум интерференционной картины, и при регистрации интерференционной картины на фотопластине видность полос в этом месте экрана будет близка к нулю. В этом случае интерференционные полосы «смажутся».

Если же полоса «бегает» заметно меньше, чем на ширину полос, то при усреднении по времени на фотопластине останутся четкие полосы.

На экране есть, или может быть, одна полоса, которая при изменении частоты света «не бегает» по экрану вовсе. Это светлая полоса, для которой оптическая разность хода равна нулю, — так называемая нулевая полоса. Нулевая полоса «не смазывается» при любой спектральной ширине источника света, так как при нулевой разности хода для любой частоты света интерферирующие волны окажутся в одинаковой фазе и дадут светлую полосу.

Если одна из интерферирующих волн по дороге от источника света испытала отражение с потерей полуволны, то нулевая полоса будет темной.

Таким образом, при интерференции квазимонохроматического света на экране одна часть интерференционной картины «смазывается», другая остается с высоким контрастом (видностью) полос. Поэтому в задачах на тему «Интерференция квазимонохроматического света» часто ставится вопрос определения области на экране, где интерференционная картина «не смазывается», либо по известным размерам этой области требуется найти параметры задачи, от которых эта область зависит. При рассмотрении этой области удобно использовать понятие «порядок интерференции».
Порядок интерференции
Номер интерференционной полосы (от нулевой полосы) — это порядок интерференции. Для полосы с номером m разность хода интерферирующих волн равна m.

Если шумит частота света, то шумят и длина волны, и число длин волн, которое укладывается на оптической разности хода для фиксированной точки экрана, и порядок интерференции m.
Если порядок интерференции шумит на единицу (m = 1), то на единицу шумит и номер интерференционной полосы для выбранной точки экрана. Этому соответствует шумовое перемещение интерференционной картины на расстояние, равное ширине полосы. При таком перемещении интерференционная картина полностью «смазывается». Найдем теперь, какое изменение частоты и длины волны света соответствует изменению порядка интерференции на единицу.

Область высокой видности интерференционной картины

при квазимонохроматическом источнике света

На границе «несмазанной» области интерференционной картины порядок интерференции m шумит на единицу (dm = 1). Произведение m равно разности хода и, следовательно, не шумит. Тогда (m) = 0. Отсюда m+m  0 и m/m  /, если m и  считать малыми положительными величинами.
Аналогично, из условия  = c/n = const следует /  /, где / — относительная ширина спектральной линии излучения.
Из равенства m/m = / = / с учетом m = 1 получаем два новых условия границы «несмазанной» области интерференционной картины:

= и = .

Если теперь учесть, что порядок интерференции — это разность хода, выраженная в длинах волн (m = /), то разность хода

 = ,

определяет границу области экрана, в которой хорошо различимы интерференционные полосы.
Далее, для решения конкретной задачи нужно найти область на экране, где разность хода не превышает заданной величины  2 /. Эта задача либо чисто геометрическая, либо — геометрической оптики. Если требуется найти максимальное число наблюдаемых интерференционных полос, то оно либо равно максимальному порядку интерференции (m = / = /), если наблюдаются полосы в одну сторону от нулевой полосы, либо — вдвое больше порядка интерференции.

Временная когерентность
Временная когерентность связана с когерентностью вдоль луча. Когерентность — это способность к интерференции. Рассмотрим две точки на одном луче как два возможных вторичных источника света для наблюдения интерференционной картины. При этом расстояние от каждой из точек до мысленного экрана предполагается одинаковым.
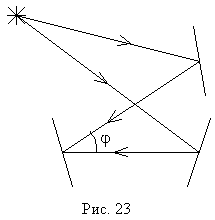
Возможный вариант оптической схемы приведен на рис. 23. Здесь A и B — две выбранные вдоль луча точки, в которые мысленно поместим полупрозрачные пластинки для получения интерференционной картины на экране C. По условию задачи AC = BC.

Рис. 23
Оптическая разность хода для интерферирующих лучей 1 и 2, как видно из рис. 23, равна AB. Если AB превышает величину  2 /, то, как указывалось выше, интерференционная картина «смазывается», и, следовательно, вторичные источники света в точках A и B оказываются некогерентными. Расстояние между точками A и B, при котором это начинает происходить, называется длиной когерентности вдоль луча (продольной когерентности). Обозначим его как L_||, тогда
L_|| = .
Эта формула часто используется при решении задач.
Наряду с понятием «продольная когерентность», используется близкое ему понятие «временная когерентность». Фаза светового поля в точке A (см. рис. 23) в момент времени t равна фазе поля в точке B в момент t+, где  — время распространения света от A до B. Следовательно, когерентность поля в точках A и B в один момент времени t точно такая же, как когерентность в одной точке B, но в два разных момента времени t и t+.
Время , за которое свет проходит длину когерентности L_||, называется временем когерентности. Из известного выражения для скорости света c/n = , получим простое соотношение для времени когерентности:
 = L_|| =  =  =  = .
Можно посмотреть на когерентность светового поля в точках A и B несколько иначе. Длина волны шумит. Следовательно, шумит число длин волн, которое укладывается на отрезке AB. Пропорционально шумит разность фаз в точках A и B. Результат интерференции зависит от разности фаз. Если разность фаз в точках A и B шумит больше, чем на 2, то поле в этих точках некогерентно, если меньше, то поле когерентно. В такой форме условие когерентности поля в точках A и B не требует расположения этих точек вдоль луча или рассмотрения поля в них в один момент времени.
Подчеркнем, что условие «разность фаз шумит больше, чем на 2» не следует путать с условием «разность фаз больше, чем 2».

Пространственная когерентность — это когерентность света в направлении, перпендикулярном лучу (поперек луча). Получается, что это когерентность разных точек поверхности равной фазы. Но на поверхности равной фазы разность фаз равна нулю и, казалось бы, не шумит. Это не совсем так. Реальный источник света не точечный, поэтому поверхность равных фаз испытывает шумовые повороты, оставаясь в каждый момент времени перпендикулярной направлению на излучающий в данный момент точечный источник света, расположенный в пределах реального источника света. Повороты поверхности равной фазы вызваны тем, что свет в точку наблюдения приходит то от одной, то от другой точки источника.

Видность интерференционной картины

с протяженным источником света

Рассмотрим оптическую схему опыта Юнга (рис. 24). Если источник света не точечный и имеет размер b поперек луча, то интерференционная картина несколько «смазывается», потому что каждый точечный источник, из которых состоит источник света, дает свою интерференционную картину, и эти картины несколько сдвинуты друг относительно друга.

Рис. 24
Будем считать, что источник света представляет собой полоску постоянной ширины и яркости. Картина полностью «смажется», если интерференционные картины от крайних точек источника будут сдвинуты относительно друг друга ровно на одну полосу интерференции, что соответствует изменению разности хода на одну длину волны .

Из рис. 24 видно, что при переходе от одной точки источника света к другой разность хода может измениться только слева от экрана с двумя щелями. Выясним, какому перемещению b точечного источника на рис. 24 соответствует изменение разности хода на .

Представим себе, что свет на рис. 24 идет справа налево. Тогда слева получим полосы интерференции от двух щелей. Переход от одной полосы к другой соответствует изменению разности хода на . Именно такая разность хода нас интересует для определения размера источника света b. То есть, размер источника b, когда свет распространяется слева направо, равен ширине полос, когда свет распространяется справа налево. Ширина полос равна /, где  — угол, под которым сходятся лучи справа налево или расходятся слева направо. Если угол  мал, то  = L₂/L₁. Тогда ширина полос равна L₁/L₂. Это и есть интересующий нас размер источника b:
b = ,
при котором интерференционные полосы полностью «смажутся».
Связь пространственной когерентности и

углового размера источника света
Если интерференционная картина на экране (см. рис. 24) «смазывается» при размере источника b, то L₂ — размер поперечной когерентности света в месте расположения экрана с двумя щелями. Действительно, две щели — это две точки на фронте волны, которые являются вторичными источниками света. Интерференционная картина пропадает, если вторичные источники света некогерентны. Они некогерентны, если расположены на расстоянии, большем или равном длине пространственной когерентности.

Перепишем теперь формулу для размера источника в виде соотношения

= .
Здесь b/L₁ — угловой размер источника при его наблюдении из точки, в которой размер пространственной когерентности равен L₂. Эта формула позволяет определять угловые размеры звезд через измерение длины пространственной когерентности их света.

Перепишем последнюю формулу в следующем виде:
= .
Здесь L₂/L₁ — угол (см. рис. 24), под которым выходят из источника света лучи, интерферирующие на экране. Этот угол называется апертурой интерференции. Теперь формула
 =
означает, что максимальная апертура интерференции равна отношению длины волны к размеру источника света. Если апертура больше, то нет интерференции. Свет из источника размером b выходит когерентно в любой угол /b.

Рассмотрим две точки, через которые проходит свет. Если проекции этих точек на направление светового луча удалены друг от друга меньше, чем на длину продольной когерентности, и если их проекции на плоскость, перпендикулярную лучу, удалены друг от друга меньше, чем на радиус поперечной когерентности, то данные две точки принадлежат одному объему когерентности.
Рассмотрим еще раз схему опыта Юнга и проследим перемещение объема когерентности вдоль лучей.

Рис. 25
Сначала объем когерентности «распространяется» из источника света в угол /b (рис. 25,а).

Затем края этого объема «просачиваются» через две щели (рис. 25,б). Если объем когерентности не накрывает сразу обе щели, то не будет интерференционной картины на экране, так как в этом случае недостаточна пространственная когерентность на фронте, проходящем через две щели, и щели как вторичные источники света некогерентны.

После щелей получаются два объема одной когерентности (рис. 25,в).

Эти два объема приходят в интересующую нас точку A экрана либо почти одновременно, заметно перекрываясь, как на рис.25,г, либо приходят по очереди, как на рис. 25,д. В первом случае в данной точке экрана интерференционная картина «не смазана», а во втором — «смазана». В этих двух вариантах видность картины определяется временной когерентностью, длиной объема когерентности вдоль луча.
Интерференция двух волн возможна тогда и только тогда, когда свет, пройдя двумя путями, попадает на экран так, что объем когерентности перекрывается сам с собой. Чем больше он перекрывается, тем больше видность интерференционной картины.

Совместное влияние временной и пространственной когерентности

на интерференционную картину

При равных интенсивностях интерферирующих волн зависимость видности интерференционной картины от номера полосы позволяет оценить порознь пространственную и временную когерентность света в месте расположения вторичных источников интерферирующего света или оценить размер и немонохроматичность источника света.

Видность вблизи нулевой полосы определяется только пространственной когерентностью, а изменение видности с номером полосы определяется временной когерентностью источника света.

Локализация интерференционной картины

Интерференция света, отраженного от тонкой прозрачной пленки, является важным частным случаем получения интерференционной картины методом деления амплитуды. В случае протяженного источника света интерференционная картина может быть получена либо очень близко к поверхности пленки, либо очень далеко от пленки, как говорят, на бесконечности. Соответственно говорят об интерференционной картине локализованной на поверхности пленки и на бесконечности. Как показывает опыт, в промежуточных положениях экрана интерференционная картина оказывается размытой.

Удаленный объект отображается собирающей линзой в ее фокальной плоскости. Оказывается, интерференционную картину, локализованную на бесконечности, можно также наблюдать в фокальной плоскости линзы.

Линза позволяет наблюдать и кольца Ньютона, локализованные в плоскости между плоской поверхностью стекла и соприкасающейся с ней выпуклой поверхностью линзы. Если экран физически поставить между соприкасающимися поверхностями, то до одной из них свет просто не дойдет, и интерференции не будет.

Линза отображает локализованную в плоскости касания интерференционную картину в виде колец Ньютона на экран по законам геометрической оптики:
= + ,
Здесь f — фокусное расстояние линзы, a — расстояние от плоскости локализации интерференционной картины до линзы, b — расстояние от линзы до изображения интерференционной картины на экране. Интерференционная картина в плоскости локализации играет роль светящегося тела.

Интерферируют те лучи, которые выходят из одной точки источника и попадают в одну точку плоскости локализации интерференционной картины. Неважно, что в этой плоскости нет экрана, и что после плоскости лучи расходятся. Линза собирает их на экране с той же разностью фаз, которую они имели в плоскости локализации интерференционной картины. Поэтому светлая полоса изображается в светлую, а темная в темную.

Интерференционную картину можно наблюдать вообще без экрана. При этом хрусталик глаза играет роль линзы, а сетчатка — роль экрана. Интерференционную картину, локализованную на бесконечности, можно рассматривать в подзорную трубу, а локализованную в другой плоскости можно рассматривать через окуляр, как рассматривают близко расположенные мелкие предметы.
Есть, правда, некоторое отличие между наблюдением интерференционной картины на экране и интерференционной картины локализованной в пространстве.
На экране интерференционную картину можно рассматривать с разных сторон. Для наблюдения интерференционной картины, локализованной в пространстве, линзу окуляра (или глаз) можно поставить только по ходу лучей, причем через линзу должны проходить оба интерферирующих луча, как, например, на рис.26. Если через линзу проходит только один из интерферирующих лучей (рис. 27), то изображения интерференционной картины не будет. Вместо полос будет серый фон освещения одним лучом.

Рис. 26

Рис. 27

Полосы равной толщины и полосы равного наклона
Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.

Полосы равного наклона локализованы на бесконечности.

Полосы равной толщины локализованы в плоскости, отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.
Для наблюдения полос равной толщины отражающие поверхности не обязательно должны быть идеально плоскопараллельны. Пара отражающих плоскостей может образовывать тонкий клин. Могут быть соприкасающиеся поверхности, одна или обе из которых сферические (кольца Ньютона).
Более того, две отражающих поверхности могут быть расположены в разных местах, как в интерферометре Майкельсона (рис.28). Здесь S — источник света, P — экран для наблюдения интерференции отраженных волн от зеркал 1 и 2, 3 — полупрозрачная пластинка. Если зеркало 2 мысленно отразить в полупрозрачной пластинке 3, то его изображение примет положение 2′. Вместе с зеркалом 2 мысленно отобразим в полупрозрачной пластинке и все лучи, идущие справа от нее к зеркалу 2 и от него обратно к полупрозрачной пластинке. Тогда на экран P свет будет приходить, как бы отражаясь от двух плоскостей 1 и 2′. Если дополнить интерферометр двумя линзами, как это обычно делается (рис. 29), то, в зависимости от расстояния между линзой L₂ и экраном P, можно наблюдать полосы равной толщины (1/a₁ + 1/a₂ = 1/f₂) или полосы равного наклона (a₂ = f₂).

Рис. 29

Рис. 28

ДИФРАКЦИЯ
Дифракция — это огибание светом препятствий. Например, в опыте Юнга свет за каждой щелью распространяется не только в том направлении, в котором он распространялся до щели.

Возможность дифракции связана с тем, что свет за каждой щелью распространяется так, как если бы в плоскости щели находилась совокупность вторичных точечных источников света (принцип Гюйгенса). Правда, эти вторичные источники охотнее излучают в направлении, в котором свет распространялся до щели, чем в другие направления.

В произвольную точку за щелью свет от разных вторичных источников приходит в разных фазах. В каких–то направлениях при сложении этих волн в результате интерференции получаются колебания поля E с большой амплитудой, а в каких–то с малой амплитудой. В соответствии с этим говорят, что свет при дифракции на щели в одних направлениях распространяется, а в других — нет.

Полученное в результате дифракции распределение интенсивности по экрану называется дифракционной картиной.
Комплексная амплитуда световой волны
Пусть напряженность электрического поля E световой волны в некоторой точке изменяется по закону
E = E₀cos(t).
Поставим в соответствие этой вещественной функции E некоторую комплексную функцию E’, которую будем называть комплексной напряженностью поля световой волны:
E’ = E₀exp<i(t)>,
где i — мнимая единица, а знак минус перед i — вопрос соглашения. Назовем величину E₀exp(i) — комплексной амплитудой световой волны.

Вещественная (настоящая) напряженность поля световой волны E равна вещественной части придуманной нами комплексной напряженности E’.

Возникает вопрос, насколько однозначно это сопоставление.

Действительно, есть неоднозначность сопоставления комплексного числа вещественному, но для аналитической функции, например гармонической (косинусоидальной), эта неоднозначность пропадает. Если вещественная функция в окрестности некоторой точки разлагается в ряд Тейлора, то эту функцию с помощью этого ряда однозначно можно продолжить на комплексную плоскость.

Зачем нужна комплексная напряженность поля?

Сложение комплексных напряженностей можно сделать наглядным. Комплексное число можно представить себе как вектор на комплексной плоскости и складывать комплексные напряженности по правилам сложения векторов. Сумма вещественных напряженностей может быть получена как вещественная часть суммы комплексных напряженностей.

Для монохроматического света (света одной частоты) можно складывать не комплексные напряженности, а комплексные амплитуды, так как одни от других отличаются одинаковым для всех слагаемых множителем exp(it). Комплексная амплитуда суммы волн равна сумме комплексных амплитуд.

Складывая комплексные амплитуды волн, излучаемых вторичными источниками, мы можем найти комплексную амплитуду поля в любой точке за щелью. Длина этого вектора на комплексной плоскости равна амплитуде вещественного поля E, а направление определяет сдвиг фазы колебаний вещественного поля.

Все приемники света в оптическом диапазоне регистрируют интенсивность света, а не напряженность поля световой волны. Интенсивность света равна квадрату модуля комплексной амплитуды поля с коэффициентом c/8 в системе единиц СГС Гаусса для линейной поляризации света. Часто в задачах интересуются отношением интенсивностей, в этом случае постоянный сомножитель несуществен.

Итак, задача по дифракции обычно сводится к векторному сложению комплексных амплитуд вторичных источников света. От чего же зависят величины и фазы этих комплексных амплитуд?

Согласно дифракционной формуле Френеля–Кирхгофа [3] комплексная амплитуда вторичного источника света в точке наблюдения может быть выражена по формуле
dE_p’ = E_s’(cos ₁ + cos ₂)dS.
Здесь E_s’ — комплексная амплитуда поля в точке расположения вторичного источника света, dS — площадь излучающей поверхности вторичного источника, r — расстояние от вторичного источника до точки наблюдения, k = 2/ — волновое число, ₁ — угол между нормалью к поверхности вторичного источника и направлением распространения света к точке вторичного источника, ₂ — угол между нормалью к поверхности вторичного источника и направлением от вторичного источника к точке наблюдения.
В задачах по дифракции зависимостью амплитуды поля от направления излучения вторичного источника света обычно пренебрегают, что справедливо для малых углов дифракции.
Амплитуда излучения вторичного источника обратно пропорциональна расстоянию от вторичного источника до точки наблюдения, но в задачах по дифракции и этой зависимостью обычно пренебрегают. Последнее связано с тем, что в приближении малых углов дифракции различные точки экрана почти одинаково удалены от вторичного источника. Поэтому в выражении для комплексной амплитуды оставляют быстро меняющийся сомножитель exp(ikr), заменяя медленно меняющийся с расстоянием сомножитель 1/r константой.
Амплитуда вторичного источника света пропорциональна площади источника. При решении задач это обычно учитывают так, что мысленно разбивают щель или другой вторичный источник на источники света одинаковой площади, считая при этом, что они излучают волны, которые в точке наблюдения имеют одинаковые амплитуды, но разные фазы. Тогда векторы комплексных амплитуд будут по–разному ориентированы на комплексной плоскости. Угол поворота относительно оси X равен фазе комплексного числа.

Фазовый множитель комплексной амплитуды равен exp1+r₂)>, где k = 2/ — волновое число, r₁ — расстояние от истинного источника до вторичного источника, r₂ — расстояние от вторичного источника до точки наблюдения. Следовательно, угол поворота на комплексной плоскости равен k(r₁+r₂).
Ключевые моменты решения задач по теме «дифракция»
Обычно в задаче по теме «дифракция» требуется найти интенсивность дифрагированной волны в некоторой точке или в некотором направлении.

Интенсивность равна квадрату модуля комплексной амплитуды с коэффициентом c/8.

Комплексную амплитуду можно найти как векторную сумму комплексных амплитуд световых волн, пришедших от разных частей щели или другого вторичного источника света. Части удобно брать одинаковой площади.

Сумма амплитуд — это сумма (интеграл) маленьких векторов равной длины (для равных площадей разбиения вторичного источника), но по–разному ориентированных.

Угол поворота каждого вектора относительно оси X на комплексной плоскости равен kr = 2r/, где r = r₁ + r₂.

В качестве примера рассмотрим дифракцию Фраунгофера на одной щели.
Дифракция на одной щели
Рассмотрим дифракцию плоской монохроматической волны на щели, плоскость которой перпендикулярна направлению распространения волны.

Все вторичные источники в плоскости щели имеют одинаковую фазу. Поэтому при вычислении фазы излучения в точке наблюдения на экране за щелью остается учесть разность фаз, которая «набегает» от щели до экрана. Будем считать, что экран находится далеко от щели, что соответствует дифракции Фраунгофера. Подробнее дифракция Фраунгофера обсуждается ниже.

Рис. 30
Если экран далеко, то можно считать, что точки на пунктирной прямой AB (рис. 30) одинаково удалены от точки наблюдения. Тогда для участка щели с координатой, равной y, расстояние до точки наблюдения равно ysin  плюс несущественная константа.
С изменением y—коорди­наты линейно меняется расстояние до экрана, а значит — фаза поля, и угол поворота комплексной амплитуды на комплексной плоскости. Если мы мысленно разобьем щель на тонкие полоски одинаковой ширины dy, то одинаковые по модулю комплексные амплитуды от соседних полосок в точке наблюдения будут развернуты друг относительно друга на равные углы (2/)dysin . Складывая много маленьких векторов, мы получим картину их выстраивания в дугу окружности, так как одинаковы амплитуды векторов и одинаковы углы поворота между соседними векторами (рис. 31).

Рис. 31

Векторная сумма — вектор, проведенный из начала первого вектора в конец последнего. Если суммируемые векторы образуют дугу окружности, то результирующий вектор — ее хорда.

Интенсивность равна квадрату длины этой хорды и не изменяется при повороте комплексных амплитуд на комплексной плоскости. Следовательно, интенсивность не зависит от общего поворота векторов на рис. 31. Поэтому ориентацию начального вектора суммы можно выбрать произвольно. Обычно первый вектор направляют вдоль оси X.

Обсудим, что изменится в картине сложения амплитуд на комплексной плоскости при изменении направления регистрации света.

Изменение угла  между направлением наблюдения и нормалью к плоскости щели приводит к изменению угла d на комплексной плоскости между векторами комплексных амплитуд волн, пришедших в точку наблюдения от соседних участков щели:
d = dysin .
При сложении векторов на комплексной плоскости это приводит к изменению радиуса дуги окружности при сохранении длины дуги. Дуга несколько сворачивается или разворачивается (рис.32).

Рис. 32
Длина дуги равна сумме модулей комплексных амплитуд волн, пришедших от разных участков щели, поэтому она сохраняется при изменении направления наблюдения .

При условии  = 0 дуга окружности разворачивается в прямую линию, что соответствует максимуму дифракционной картины, а квадрат длины дуги определяет интенсивность света в максимуме.

Если изменять интенсивность падающей волны, то картина сложения амплитуд дифрагированных волн будет меняться так, как изображено на рис. 34.

Рис. 33

Дифракционная решетка
Рассмотрим простейшую дифракционную решетку, работающую на пропускание. Эта решетка представляет собой плоский экран с чередующимися прозрачными и непрозрачными полосами. Все прозрачные полосы имеют одинаковую ширину, скажем a. Все непрозрачные полосы также имеют одинаковую ширину — b. Сумма a+b = d называется шагом решетки. Общее число штрихов решетки обозначим N. Тогда ширина решетки равна произведению Nd.

Рассмотрим простейший случай дифракции плоской монохроматической волны, которая падает на решетку перпендикулярно ее плоскости, а распределение интенсивности дифрагированной волны нас будет интересовать на очень удаленном экране или, как говорят, на бесконечности.

Главный дифракционный максимум образуется при условии, что волны от соседних штрихов решетки приходят в точку наблюдения в одинаковой фазе или со сдвигом фаз, кратным 2. Соответствующая разность хода должна быть кратна :
dsin  = m,
где m — целое число. Это основная формула дифракционной решетки. Если угол падения света на решетку не равен нулю, то
d(sin ₁ + sin ₂) = m,
где ₁ — угол падения, ₂ — угол дифракции.

Какова амплитуда дифрагированной волны в том случае, если разность фаз волн от соседних штрихов мало отличается от величины, кратной 2? Добавление к разности фаз величины, кратной 2, не изменяет результат интерференции волн, поэтому будем считать, что разность фаз мало отличается от нуля. Амплитуда света от каждого штриха одна и та же. Разность фаз между волнами от соседних штрихов также одинакова. Число штрихов велико. Тогда картина сложения амплитуд на комплексной плоскости полностью аналогична картине сложения амплитуд при дифракции на одной щели. Векторы комплексных амплитуд будут лежать на дуге окружности.

При изменении направления наблюдения  дуга окружности будет несколько сворачиваться или разворачиваться в дугу меньшего или большего радиуса при сохранении длины дуги.

Направление главного максимума соответствует условию, когда дуга разворачивается в прямую линию.
Если дуга сворачивается в окружность, то интенсивность света в этом направлении равна нулю. При этом разность фаз волн от первого и последнего штрихов решетки равна 2. Следовательно, разность фаз волн двух соседних штрихов равна 2/N, что в N раз меньше разности фаз, соответствующей следующему главному максимуму.
Таким образом, ширина главного максимума примерно в N раз меньше расстояния между главными максимумами, где N — число штрихов решетки. Это соотношение полезно помнить при решении задач.
Если мы рассматриваем главный максимум с номером m, то угол, соответствующий направлению на главный максимум, примерно в mN раз больше угловой ширины главного максимума. Отсюда следует выражение для относительного спектрального разрешения решетки в m–м порядке дифракции:
= .
Эта формула часто используется при решении задач.
Мы выяснили, что при изменении угла дифракции  от значения угла, соответствующего главному максимуму, до некоторого близкого значения, при котором интенсивность дифрагированной волны обращается в нуль, картина сложения амплитуд изменяется от прямой линии до окружности. Что происходит при дальнейшем изменении угла ?
Дуга сворачивается дальше, а когда она превращается в полторы окружности, суммарная амплитуда достигает более «мелкого» максимума. Это так называемый побочный максимум. Следующий побочный максимум появится, когда дуга свернется в две с половиной окружности и т.д.

В качестве задачи можно определить, сколько побочных максимумов между двумя главными максимумами и как зависит отношение амплитуды побочного максимума к амплитуде главного максимума от номера побочного максимума.

Обсудим теперь, какова амплитуда волны в направлении главного максимума. Эта амплитуда равна произведению числа штрихов решетки на амплитуду волны, дифрагированной в данном направлении от одного штриха.
Оказывается, при некоторых условиях амплитуда главного максимума может оказаться равной нулю. Эта ситуация может обыгрываться в задачах.
В первом порядке дифракции амплитуда главного максимума не может быть равна нулю, поэтому рассмотрим второй порядок дифракции. Во втором порядке разность хода от соседних штрихов равна 2, что соответствует разности фаз 4, которая «набегает» при перемещении по вторичным источникам света поперек штрихов от начала одного штриха до начала соседнего штриха.
Разность фаз 4 соответствует двум окружностям дуги сложения амплитуд на комплексной плоскости. Только теперь надо рассматривать не сложение амплитуд от разных штрихов, а сложение амплитуд от тонких полосок внутри одного штриха.

Источник