Что такое правильная четырехугольная призма
Что такое призма: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение призмы
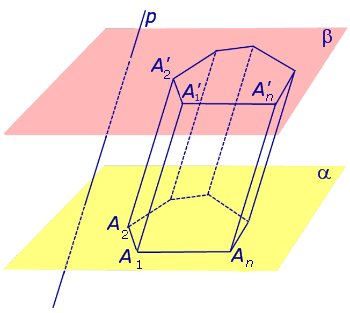
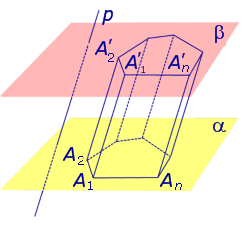
Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.
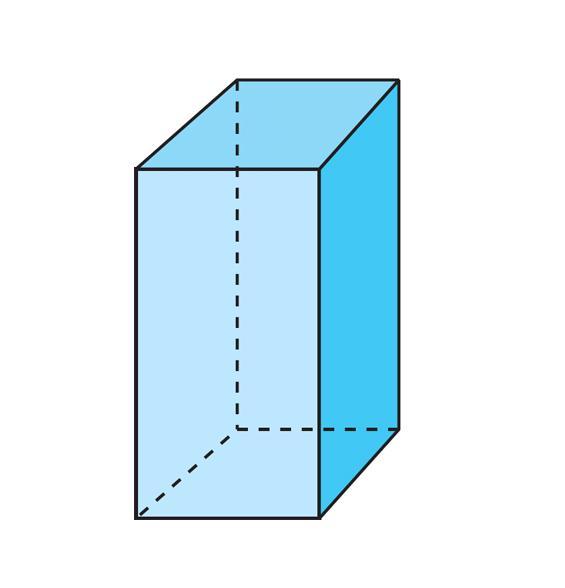
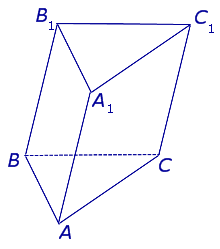
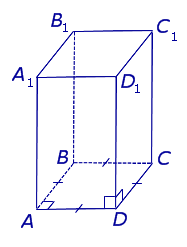
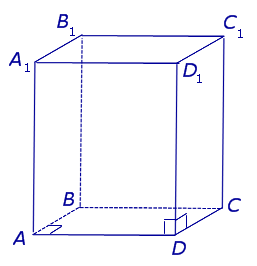
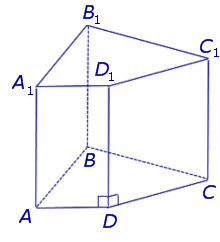
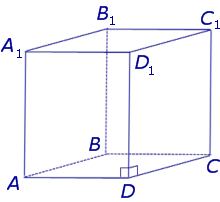
На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.
Элементы призмы
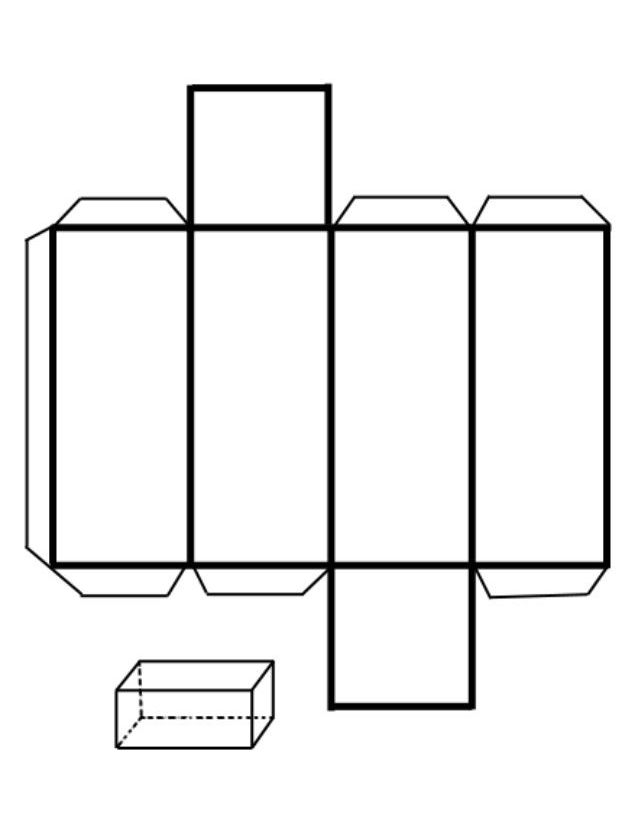
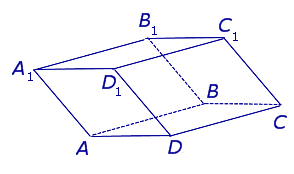
Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:
Примечание: свойства призмы представлены в отдельной публикации.
Варианты сечения призмы
Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.
Виды призм
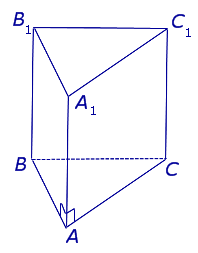
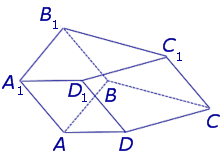
Рассмотрим разновидности фигуры с треугольным основанием.
Призма и ее элементы. Свойства правильной четырехугольной призмы
Призма является достаточно простой геометрической объемной фигурой. Тем не менее у некоторых школьников при определении ее основных свойств возникают проблемы, причина которых, как правило, связана с неправильно используемой терминологией. В данной статье рассмотрим, какие призмы бывают, как они называются, а также подробно охарактеризуем правильную четырехугольную призму.
Призма в геометрии

Элементы призмы и теорема Эйлера
Поскольку рассматриваемая объемная фигура представляет собой полиэдр, то есть образована набором пересекающихся плоскостей, то она характеризуется некоторым количеством вершин, ребер и граней. Все они являются элементами призмы.
В середине XVIII века швейцарский математик Леонард Эйлер установил связь между количеством основных элементов полиэдра. Эта связь записывается следующей простой формулой:
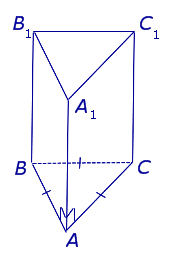
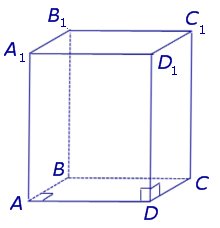
Для любой призмы справедливо это равенство. Приведем пример его использования. Предположим, имеется правильная четырехугольная призма. Она изображена на рисунке ниже.
Видно, что число вершин для нее равно 8 (по 4 для каждого четырехугольного основания). Число сторон, или граней составляет 6 (2 основания и 4 боковых прямоугольника). Тогда количество ребер для нее будет равно:
Все их можно посчитать, если обратится к тому же рисунку. Восемь ребер лежат в основаниях, а четыре ребра перпендикулярны этим основаниям.
Полная классификация призм
С этой классификацией важно разобраться, чтобы впоследствии не путаться в терминологии и использовать правильные формулы для вычисления, например, площади поверхности или объема фигур.
Для любой призмы произвольной формы можно выделить 4 признака, которые ее будут характеризовать. Перечислим их:
Из всех этих пунктов хотелось бы остановиться подробнее на последнем. Прямая призма также называется прямоугольной. Связано это с тем, что для нее параллелограммы являются прямоугольниками в общем случае (в некоторых случаях они могут быть квадратами).
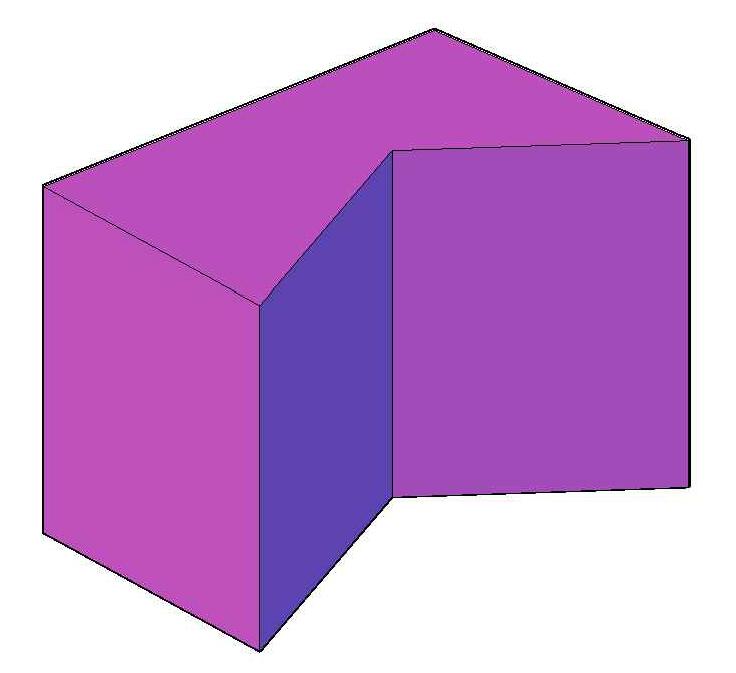
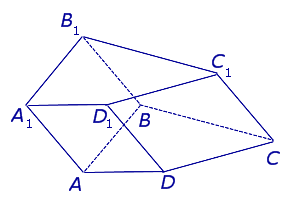
Для примера на рисунке выше изображена пятиугольная вогнутая прямоугольная, или прямая фигура.
Правильная четырехугольная призма
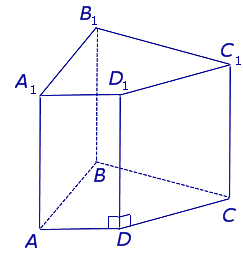
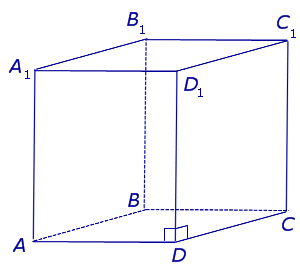
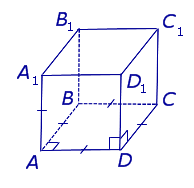
Основание этой призмы представляет собой правильный четырехугольник, то есть квадрат. Выше на рисунке уже было показано, как выглядит эта призма. Помимо двух квадратов, которые ее ограничивают сверху и снизу, она также включает 4 прямоугольника.
Обозначим сторону основания правильной четырехугольной призмы буквой a, длину ее бокового ребра обозначим буквой c. Эта длина также является высотой фигуры. Тогда площадь всей поверхности этой призмы выразится формулой:
S = 2*a2 + 4*a*c = 2*a*(a + 2*c)
Учитывая введенные обозначения для длин сторон, запишем формулу для объема рассматриваемой фигуры:
То есть объем вычисляется как произведение площади квадратного основания на длину бокового ребра.
Фигура куб
Все знают эту идеальную объемную фигуру, но мало кто задумывался, что она представляет собой правильную четырехугольную призму, сторона которой равна длине стороны квадратного основания, то есть c = a.
Для куба формулы полной площади поверхности и объема примут вид:
Призмы
Основные определения и свойства призм. Теорема Эйлера
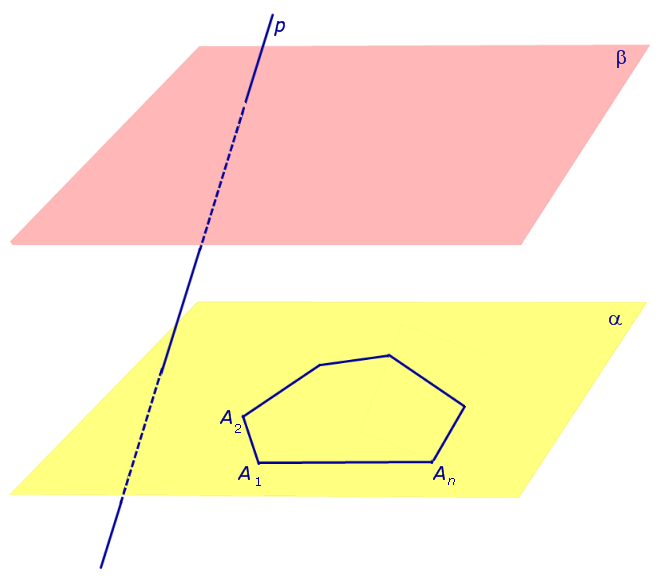
Утверждение 1. Каждый из n четырехугольников
Для остальных четырехугольников доказательство проводится аналогично.
Это утверждение непосредственно вытекает из утверждения 1.
Замечание 1. В случае, когда не требуется делать специальных уточнений,
боковые грани и основания призмы называют гранями призмы
совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы,
n – угольные призмы называют призмами.
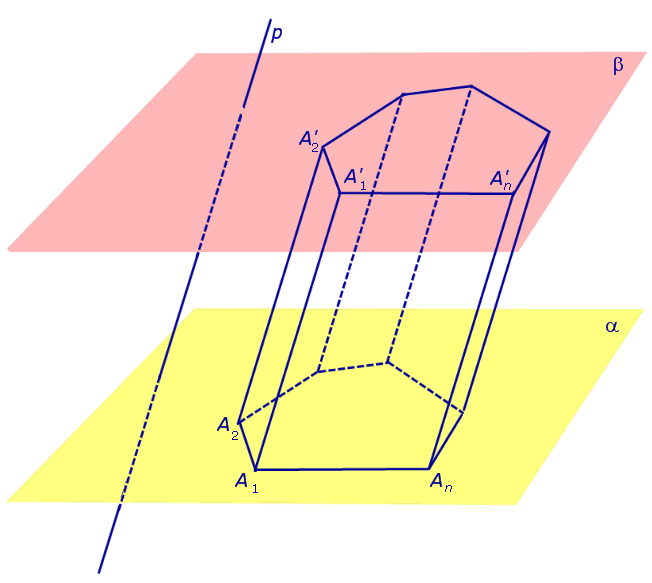
Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
то теорема Эйлера доказана.
Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
Виды призм. Прямые и наклонные призмы. Правильные призмы
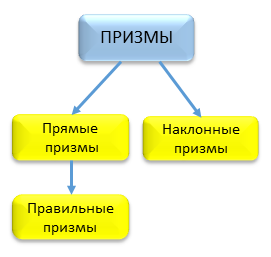
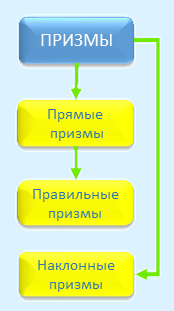
Существует следующая классификация призм.
Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.
Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.
Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.