Что такое правильная дробь и неправильная дробь 6 класс
Правильные и неправильные дроби.
Виды дробей.
Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)
Делятся дроби на два вида правильные дроби и неправильные дроби.
В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)
В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Единицу мы можем представить как дробь \(1 = \frac<3><3>\)
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)
Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.
Правильные и неправильные дроби
Обыкновенные дроби делятся на правильные и неправильные.
Правильные дроби
Правильная дробь — это обыкновенная дробь, у которой числитель меньше знаменателя.
Чтобы узнать является ли дробь правильной, надо сравнить её члены между собой. Члены дроби сравниваются в соответствии с правилом сравнения натуральных чисел.
Пример. Рассмотрим дробь:
у которой 7 — это числитель, а 8 — знаменатель. Сравним числитель со знаменателем:
7 Пример 1. Рассмотрим дробь:
у которой 8 — это числитель, а 7 — знаменатель. Сравним числитель со знаменателем:
Так как числитель больше знаменателя, значит данная дробь является неправильной.
Пример 2. Рассмотрим дробь:
Сравним числитель со знаменателем:
Так как числитель равен знаменателю, значит данная дробь является неправильной.
Любая неправильная дробь больше единицы или равна ей:
Обратите внимание, что любое натуральное число можно представить в виде неправильной дроби, следующим образом:
Дробь с числителем p и знаменателем 1 – это другая форма записи натурального числа p: 
Число 0 принято считать равным дроби вида 
Любую неправильную дробь, у которой числитель больше знаменателя можно представить в виде смешанного числа.
Сравнение правильных и неправильных дробей
Любая неправильная обыкновенная дробь больше правильной, так как правильная дробь всегда меньше единицы, а неправильная больше единицы или равна ей.
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
Дроби
Что такое дробь
Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.
Дробная черта равносильна знаку деления. То есть \(4:6=\frac46\) (четыре шестых), \(7:2=\frac72\) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Знаменатель дроби не может быть нулем.
Основные свойства дробей
Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).
Существует два вида дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: \(\frac <39>
Правильные дроби
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого: \( \frac25
Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.
Смешанные дроби
Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.
Смешанное число — это число, содержащее целую и дробную часть.
Для составления смешанной дроби необходимо:
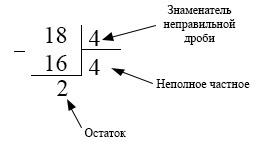
Записать неправильную дробь \(\frac<18>4\) в виде смешанной.
Тогда искомая смешанная дробь \(\frac<18>4=4\frac24.\) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:
Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.
Смешанное число \(6\frac25\) записать в виде неправильной дроби.
Как перевести правильную дробь в неправильную
Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.
Любое натуральное число можно представить в виде неправильной дроби: \(2=\frac21.\)
Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: \(p=\frac p1.\)
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби \(\frac ab\) и \(\frac cd\) к общему знаменателю, необходимо:
Сравнение
Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.
\(\frac34>\frac13,\) поскольку \(\frac9<12>>\frac4<12>.\)
Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.
К примеру, \(8\frac16>5\frac23.\)
Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: \(5\frac23>5\frac13.\)
Сложение и вычитание
Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.
При сложении смешанных чисел целые и дробные части складываются отдельно.
Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.
Умножение и деление
Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.
\(\frac ab\cdot\frac cd=\frac
Умножить дробь \(\frac35\) на \(\frac23.\)
При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде \(p=\frac p1.\)
\(\frac ab\cdot p=\frac ab\cdot\frac p1=\frac
Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.
Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.
\(\frac ab:\frac cd=\frac ab\cdot\frac dc=\frac
Поделить дробь \(\frac34\) на \(\frac23.\)
При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби.
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо: