Что такое правильная фигура

Правильные фигуры. Свойства правильных фигур. Равные фигуры

Основные понятия правильной фигуры, их свойства, периметр, а также площадь геометрической фигуры. Основные виды правильных фигур (шестиугольник, треугольник, квадрат, пятиугольник), понятие их равенства и свойств. Задачи для урока по математике.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Размещено на http://www.allbest.ru/

Открытый урок 5 класс

Правильные фигуры. Свойства правильных фигур. Равные фигуры

Учитель математики и информатики

Харлова Елена Павловна

Правильные фигуры. Свойства правильных фигур. Равенство фигур

Цели: обучающая: ввести понятие правильной фигуры; рассмотреть свойства правильных фигур, периметр и площадь; исследовать виды правильных фигур; ввести понятие равенства фигур; рассказать об основных свойствах равных фигур;

Воспитательная: воспитать интерес к геометрии;

Развивающая: развивать логическое мышление.

Тип урока: урок усвоения новых знаний.

Оборудование: учебники, тетради, чертёжные принадлежности, компьютер. правильный фигура геометрический равенство

1. Организационный момент

Приветствие учителя. Проверка готовности к уроку. Проверка присутствующих. Познакомить присутствующих с темой урока и его целью.

2. Проверка домашнего задания

Устный опрос по теме параграфа.

ь Какие виды многоугольников вы знаете?

ь Что такое треугольник?

ь Какие виды треугольников вы знаете?

ь Что такое четырёхугольник?

ь Какие виды четырёхугольников вы знаете?

ь Что такое четырёхугольник? Квадрат?

ь Что такое периметр многоугольника?

ь Чему равен периметр треугольника? Прямоугольника? Квадрата?

3. Изучение нового материала

Ввожу определение правильных фигур.

Далее вводится понятие равной фигуры.

4. Закрепление изученного материала на практике

Для закрепления нового материала предлагается решить несколько задач.

Итак, что же мы узнали нового сегодня на уроке?

Какие фигуры называются правильными?

Какие фигуры называются равными?

Все ли правильные фигуры равны?

Все ли равные фигуры правильные?

Объёмные фигуры могут быть равными?

Объёмные фигуры могут быть правильными?

О каких объёмных правильных фигурах вы знали с начальной школы?

О каких объёмных фигурах вы сегодня узнали?

Что вам понравилось больше всего на уроке?

Что было самым сложным?

Размещено на Allbest.ru

Подобные документы

Из всех прямоугольников с площадью 9 дм2 найдите тот, у которого периметр наименьший.Вычислить площадь фигуры, ограниченной линиями (сделав рисунок). Вычислить площадь фигуры, ограниченной линиями.

задача [20,9 K], добавлен 11.01.2004

Ознакомление с понятием и основными свойствами кривых постоянной ширины. Треугольник Рело: исторические сведения, очертание, площадь. Особенности движения его вершины и центра. Применение исследуемой фигуры в грейферном механизме и кинопроекторах.

курсовая работа [1,4 M], добавлен 18.01.2011

Фигуры вращения правильных многогранников, использование их теории. Виды поверхностей в фигурах вращения. Теорема о пересечении гиперболической и цилиндрической поверхностей вращения. Классификация задач на вращение многогранников и вычисление объемов.

реферат [1,1 M], добавлен 25.09.2009

Основные виды симметрии (центральная и осевая). Прямая в качестве оси симметрии фигуры. Примеры фигур, обладающих осевой симметрией. Симметричность относительно точки. Точка как центр симметрии фигуры. Примеры фигур, обладающих центральной симметрией.

презентация [2,7 M], добавлен 30.10.2014

Цепочка теорем, которая охватывает весь курс геометрии. Средняя линия фигур как отрезок, соединяющий середины двух сторон данной фигуры. Свойства средних линий. Построение различных планиметрических и стереометрических фигур, рациональное решение задач.

научная работа [2,0 M], добавлен 29.01.2010

Источник

Презентация на тему: Правильные фигуры в геометрии

Правильные фигурыв геометрии Учитель математики Беленкова Ольга Александровна

Правильные многоугольники Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

Свойства правильного многоугольника: Правильный многоугольник является вписанным в окружность и описанным около окружности. Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей. Периметры правильных n-угольников относятся как радиусы описанных окружностей.

Виды правильных многоугольников.

Правильные многогранники «Правильных многогранников вызывающе мало, – написал когда-то Л. Кэрролл – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».

Многогранник- это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника.

Существует 5 видов правильных многогранников: 1)тетраэдр2) гексаэдр3) додекаэдр4)октаэдр5)икосаэдр

Тетраэдр Свойства:Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.

Гексаэдр Свойства :Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям. В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным. В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба. Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра. В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Додекаэдр (от греческого dodeka – двенадцать и hedra – грань) Правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.

Икосаэдр Свойства:Икосаэдр можно вписать в куб, при этом, шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра. В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра. Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.

Источник

Правильные фигуры в геометрии

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Правильные фигуры
в геометрии
Учитель математики Беленкова Ольга Александровна

Описание слайда:

Правильные многоугольники
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

Описание слайда:

Свойства правильного многоугольника:
Правильный многоугольник является вписанным в окружность и описанным около окружности.
Центр правильного многоугольника совпадает с центрами вписанной и описанной окружностей.
Периметры правильных n-угольников относятся как радиусы описанных окружностей.

Описание слайда:

Виды правильных многоугольников.

Описание слайда:

Правильные многогранники
«Правильных многогранников вызывающе мало, – написал когда-то Л. Кэрролл – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».

Описание слайда:

Многогранник- это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности.
Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками.
Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника.

Описание слайда:

Существует 5 видов правильных многогранников:
1)тетраэдр
2) гексаэдр
3) додекаэдр
4)октаэдр
5)икосаэдр

Описание слайда:

Тетраэдр
Свойства:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.

Описание слайда:

Гексаэдр
Свойства :
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Описание слайда:

Додекаэдр
(от греческого dodeka – двенадцать и hedra – грань) Правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.

Описание слайда:

Описание слайда:

Икосаэдр
Свойства:
Икосаэдр можно вписать в куб, при этом, шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.

Описание слайда:

Спасибо за внимание!

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Платоновы тела. Платоновы многогранники

Какое название лежит в основе

Обратите внимание на тот, факт что в названии любого многогранника есть слово-основа.

Слово-основа

Из каких геометрических фигур можно составить

Все многогранники Платона можно представить в виде комбинации правильных многоугольников

Свойства Платоновых тел

Двугранный угол тетраэдра.

Две смежные грани тетраэдра стыкуются друг с другом под углом 70,53°.

В одной вершине тетраэдра сходятся три треугольные грани. Трёхмерный угол между тремя гранями (телесный угол тетраэдра при вершине) Ω = 0,55.

Двугранный угол октаэдра.

Две смежные грани октаэдра стыкуются друг с другом под углом 109,47°.

В одной вершине октаэдра сходятся четыре треугольные грани. Трёхмерный угол между четырьмя гранями (телесный угол октаэдра при вершине) Ω = 1,36.

Двугранный угол куба.

Две смежные грани куба стыкуются друг с другом под углом 90°.

В одной вершине куба сходятся три четырёхугольные грани. Трёхмерный угол между тремя гранями (телесный угол куба при вершине) Ω = 1,57.

Двугранный угол икосаэдра.

Две смежные грани икосаэдра стыкуются друг с другом под углом 138,19°.

В одной вершине икосаэдра сходятся пять треугольных граней. Трёхмерный угол между пятью гранями (телесный угол икосаэдра при вершине) Ω = 2,63.

Двугранный угол додекаэдра.

Две смежные грани додекаэдра стыкуются друг с другом под углом 116,57°.

В одной вершине додекаэдра сходятся три пятиугольные грани. Трёхмерный угол между тремя гранями (телесный угол додекаэдра при вершине) Ω = 2,96.

Размеры многогранников

Чтобы создать коллекцию многогранников, нам будет необходимо придерживаться определенных условий, так размеры будут сопоставимы и модели можно легко сравнить друг с другом.

Один из возможных вариантов, это создавать модели, вписываемые в сферу заданных размеров.

Стороны многоугольников для этого должны иметь следующие пропорции:

Вот как будут выглядеть в этом случае все 5 правильных многогранников.

Здесь вы можете скачать развертки для создания всех пяти Платоновых тел с размерами, позволяющими поместить каждое геометрическое тело внутрь сферы диаметром 100 мм:

Другой вариант, это задать единую длину стороны для всех многоугольников, из которых будет собрана модель. Вот каковы пропорции многоугольников, имеющих единую длину стороны:

Здесь вы можете скачать развертки для создания всех пяти Платоновых тел с размерами, позволяющими построить каждое геометрическое тело с длиной стороны 50 мм:

Готовый набор для сборки

Вы можете изготовить все пять моделей Платоновых тел воспользовавшись деталями для сборки из набора «Волшебные грани».

Для удобства сборки все модели имеют рёберную конструкцию, что позволяет собрать их даже начинающему «математику».

Размеры подобраны так, что любой из многогранников может быть вписан в сферу диаметром 110 мм.

Вращение всех правильных многогранников

Сборка многогранников их набора

Ещё один выпуск «Волшебных граней» позволяет собрать все пять моделей Платоновых тел без клея.

Вращение всех правильных многогранников

Сборка многогранников их набора

Популярное

Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.

Для Вашего удобства мы снизили стоимость доставки наборов «Волшебные грани» в разы!

Геометрическая форма коробочки издалека напоминает округлую форму, что делает акцент на сходство с мячиком. Но если присмотреться по внимательнее, то мы видим.

Предположим, вы впервые увидели на прилавке книжного магазина или на страницах в интернете издание «Волшебные грани». Хочется попробовать? Но вот вопрос, какой выпуск взять на пробу.

Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника. В качестве геометрической.

Памятник многограннику «Усечённый большой додекаэдр» был обнаружен в городе Обнинск, напротив здания «ДОСААФ» (ул.Шацкого, д.14).

Источник

ПРАВИЛЬНЫЕ ФИГУРЫ И ТЕЛА

«Пифагор преобразовал геометрию, придав ей форму свободной науки, рассматривая ее принципы чисто абстрактным образом и исследуя теоремы с нематериальной, интеллектуальной точки зрения. Именно он нашел теорию иррациональных количеств и конструкцию космических тел». Так оценивал вклад Пифагора в геометрию Прокл, и эта оценка античного философа совершенно справедлива.

В самом деле, в школе Пифагора геометрия оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически — как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию. При этом, что самое главное, свойства геометрических фигур устанавливались пифагорейцами не путем измерений, а с помощью логических доказательств.

Обладая широчайшей областью практических приложений, геометрия первой из учений пифагорейской μάθημα сбросила пелену «секретности» и стала самой популярной наукой. Впрочем, Ямвлих в «Жизни Пифагора» причины популярности геометрии представлял несколько иначе: «Вот как пифагорейцы объясняют, почему геометрия стала открыто распространяться. Это произошло по вине одного из них, который потерял деньги пифагорейской общины. После этого несчастья община позволила ему зарабатывать деньги при помощи геометрии — и геометрия получила название «Предание Пифагора». Памятуя, что в V в. до н. э. были весьма популярны софисты — странствующие учителя мудрости, вполне возможно, что и пифагорейцы не гнушались пополнять казну преподаванием.

Но каково было содержание «Предания Пифагора» — первого греческого учебника геометрии? К сожалению, мы этого не знаем. Однако сохранились фрагменты из сочинений замечательного греческого математика середины V в. до н. э. Гиппократа с ионийского острова Хиоса[42]. Так вот, в сочинениях Гиппократа Хиосского свойства плоских прямолинейных фигур предполагаются хорошо известными, тогда как свойства круга и хорд подробно изучаются. Поскольку до Гиппократа геометрией занимались только пифагорейцы, то естественно предположить, что все, что Гиппократ считает хорошо известным, было открыто пифагорейцами.

Таким образом, благодаря Гиппократу Хиосскому у нас есть основания считать, что пифагорейцы в целом построили всю планиметрию прямолинейных фигур. Они изучили свойства треугольников, прямоугольников, параллелограммов, трапеций, доказали теорему о сумме углов треугольников, теорему о стороне треугольника, лежащей против тупого угла, теоремы о равновеликости треугольников. Вершиной же планиметрии прямолинейных фигур явилось доказательство знаменитой теоремы Пифагора. Эти результаты пифагорейской геометрии, по-видимому, и составили основу I книги «Начал» Евклида, которая завершается теоремой Пифагора.

Пифагорейцы проявляли повышенный интерес к правильным фигурам и телам. Правильные геометрические формы благодаря их «правильности», т. е. наличию зеркальной или поворотной (а часто и той и другой) симметрии, как нельзя более отвечали всей пифагорейской философии о закономерном, структурно-упорядоченном гармоничном устройстве мироздания. (К этому вопросу мы еще вернемся в пп. 2.2 и 4.3.) Геометрические формы, в особенности правильные, наиболее выразительно выявляли число и как нельзя более подходили для «извлечения числа из вещей». Пифагорейцы раскладывали одни геометрические формы на другие (чаще на правильные или «несущие» какие-либо «священные» числа) и в этом видели постижение внутренней взаимосвязи явлений.

Вот почему пифагорейцы придавали особое значение доказанной ими теореме о том, что плоскость можно сплошь (т. е. без «дырок» и наложений) покрыть лишь тремя правильными многоугольниками: треугольниками, квадратами и шестиугольниками (рис. 42). Доказательство этой теоремы достаточно прозрачно, и мы его оставляем читателю. Не представляет труда и построение этих правильных фигур, а также фигур, получаемых из них удвоением сторон.

Но вот построение правильного пятиугольника уже не столь очевидно. Мы не знаем, как строили правильный пятиугольник пифагорейцы. Но известно, что пятиконечную звезду — свой главный символ и опознавательный знак — они складывали из трех равнобедренных треугольников. А это явно перекликается с методом построения правильного пятиугольника, описанным у Евклида («Начала», кн. IV, пред. 11). Так что метод Евклида, возможно, восходит к пифагорейцам. Рассмотрим его.

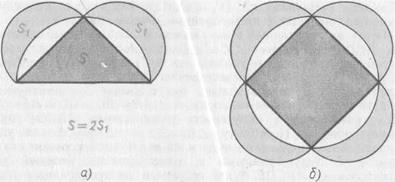
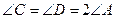Пусть дан вписанный в окружность равнобедренный треугольник ACD, у которого . (Способ построения такого треугольника мы укажем в п. 2.2.) Проведем биссектрисы CE и DB углов C и D соответственно. Тогда углы 1 — 5 (рис. 43) будут равны, а следовательно, будут равны соответствующие им дуги и стягивающие их хорды, т. е. 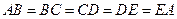. Итак, вписанный в окружность пятиугольник ABCDE будет равносторонним. Поскольку 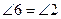и 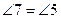как углы, опирающиеся на одинаковые дуги AE и AB соответственно, то все углы 1 — 7 будут равными и, следовательно, каждый угол пятиугольника ABCDE будет составлен из трех равных углов, т. е. 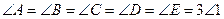. Таким образом, построенный пятиугольник является равносторонним и равноугольным, т. е. правильным.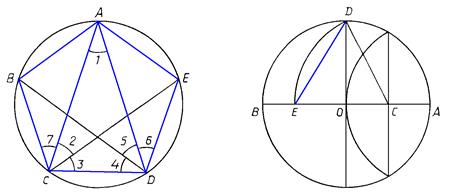

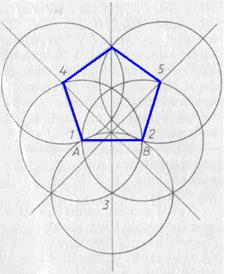
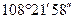Со временем древнегреческими математиками был найден более простой способ построения правильного пятиугольника. Он описан в другом выдающемся сочинении античности — «Альмагесте» Птолемея (ок. 150), которое, подобно «Началам» Евклида в геометрии, является энциклопедией античных знаний по астрономии. Птолемей делит радиус окружности OA пополам (точка C) и радиусом CD описывает окружность до пересечения с диаметром AB в точке E (рис. 44). Тогда ED и есть сторона правильного пятиугольника. (После прочтения п. 2.2 читатель без труда докажет это самостоятельно.)

Еще через полтора тысячелетия, в 1525 г., Альбрехт Дюрер (1471 — 1528), художник и ученый, один из титанов эпохи Возрождения, в трактате «Руководство к измерению при помощи циркуля и линейки» указал приближенный способ построения правильного пятиугольника по заданной стороне AB с помощью «заржавевшего» циркуля, т. е. одним раствором циркуля. Способ Дюрера понятен из рисунка 45, где цифрами последовательно обозначены положения ножки циркуля. Метод Дюрера отличается большой точностью (углы 1 и 2 равны не 108°, а , углы 4 и 5 чуть больше 107°, а угол C чуть больше 109°), так что его погрешности на глаз совершенно не воспринимаются. Сам Дюрер ни словом не обмолвился о приближенном характере своих построений, возможно, считая их точными. И тем не менее метод Дюрера является приближенным. (Попробуйте доказать это.)

А как построить с помощью циркуля и линейки следующую правильную фигуру — семиугольник? Эта задача оказалась непосильной не только древним пифагорейцам, но оставалась неразрешенной более двух тысячелетий! Лишь в 1796 г. 19-летний немецкий юноша Карл Фридрих Гаусс (1777 — 1855), прозванный позднее королем математиков, решил ее. Гаусс показал, что задача построения с помощью циркуля и линейки правильного n-угольника, равносильная задаче деления окружности на n равных частей, связана с изучением корней уравнения . 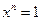Далее Гаусс доказал, что правильный N-угольник может быть построен циркулем и линейкой в том и только том случае, когда N — простое число вида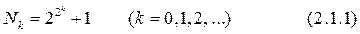

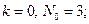
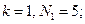
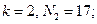
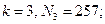
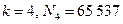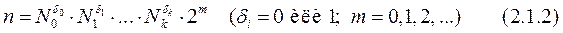
Простые числа вида (2.1.1) называются числами Ферма, и до сих пор известно лишь пять таких чисел: .

Этот результат Гаусса обобщается на случай, когда число сторон многоугольника n является произведением чисел вида (2.1.1). Учитывая также возможность удвоения n, сформулируем теорему Гаусса: правильный многоугольник можно построить с помощью циркуля и линейки тогда и только тогда, когда число его сторон имеет вид

Фактически в , так как других чисел Ферма пока неизвестно.

Так в самом конце XVIII в. была решена проблема, поставленная более 2000 лет назад пифагорейцами. Ее решение помимо гения самого Гаусса потребовало и всей суммы математических знаний, накопленных человечеством за два тысячелетия. Нам же остается лишь вновь в восхищении спросить себя: откуда у пифагорейцев была столь безупречная интуиция на «вечные» математические проблемы?

Перейдем теперь к правильным многогранникам. Их всего пять, и Прокл помимо замечательных открытий в планиметрии приписывает Пифагору построение всех пяти правильных тел. Однако сегодня историки математики предпочитают верить не Проклу, а обнаруженной схолии (σχόλιον — толкование, объяснение) в XIII книге «Начал» Евклида, где говорится, что Пифагор знал лишь три правильных тела — тетраэдр, гексаэдр (куб) и додекаэдр, а позднее Теэтет открыл и два оставшихся — октаэдр и икосаэдр. И в том и в другом случае эти античные свидетельства говорят нам об интересе пифагорейцев к правильным телам.

По-видимому, сама природа подсказала пифагорейцам форму правильных тел: кристаллы поваренной соли имеют форму куба, кристаллы квасцов — октаэдра, а кристаллы пирита — додекаэдра. Последний, как показывают раскопки в Италии, был любимой игрушкой этрусских детей во времена Пифагора.

Название правильному многограннику дается по числу его граней (например, тетраэдр — τετρά-εδρον — τετράς — четыpe + εσρα — область, часть тела, грань — четырехгранник). Правильные многогранники показаны на рисунке 46, а их геометрические характеристики собраны в таблице, где m обозначает число граней при вершине.

Правильный многогранник	Число	Геометрия грани	m
граней, M	вершин, L	ребер, N
Тетраэдр	4 (тетра)	∆
Октаэдр	8 (окто)	∆
Икосаэдр	20 (икоси)	∆
Гексаэдр	6 (гекса)	□
Додекаэдр	12 (додека)

Пифагорейцы заметили, что в кубе число вершин (8) есть среднее гармоническое числа граней (6) и числа ребер (12) и поэтому называли куб гармоническим телом. Особое предназначение куба виделось также и в том, что он единственный из правильных тел сплошь заполняет пространство.

Ко времени Евклида было замечено, что куб и октаэдр, а также додекаэдр и икосаэдр дуальны (двойственны), т. е. число граней одного тела равно числу вершин другого и наоборот. Тогда одно тело может быть получено из другого, если центры тяжести граней одного принять за вершины другого или наоборот (рис. 46). Тетраэдр дуален сам себе.

Однако важнейшее свойство выпуклых многогранников было установлено лишь в середине XVIII в. теоремой Эйлера: во всяком выпуклом многограннике число вершин (L) плюс число граней (M) минус число ребер (N) есть величина постоянная, равная двум:

К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел — они выходят далеко за рамки нашей книги. Заметим только, что строгое построение всех правильных тел было дано в XIII книге «Начал» Евклида, которая является венцом всего великого сочинения[43]. Как построение правильного многоугольника начинается с окружности, точно так же и сфера является основой для построения правильного многогранника. Как в правильном многоугольнике центры вписанной и описанной окружностей совпадают, так и в правильном многограннике совпадают центры вписанной и описанной сфер. Последнее свойство легло в основу кеплеровской модели Вселенной, которую мы рассмотрим в п. 4.3.

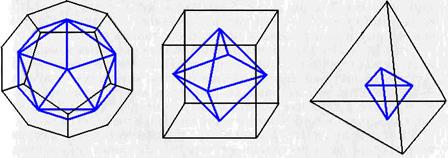
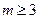И все-таки самым интригующим свойством правильных тел является то, что их существует всего пять. Не случайно доказательством этого факта завершалась последняя XIII книга «Начал» Евклида[44]. В самом деле, сумма плоских углов S при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине . Значит, гранями правильных тел могут быть только три правильных многоугольника: треугольник, квадрат и пятиугольник, ибо уже для шестиугольника 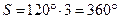. Из правильных треугольников можно составить три правильных тела: — тетраэдр, 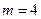— октаэдр и 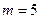— икосаэдр (при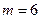 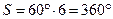). Из квадратов и правильных пятиугольников — только по одному (куб и додекаэдр) при 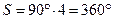(при — для квадратов и 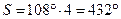— для пятиугольников). Таким образом, правильных многогранников может быть только пять.

Этот факт не мог оставить равнодушными склонных к числовой мистике пифагорейцев, а вслед за ними Платона и неоплатоников. Платон развил знаменитое учение о пяти «стихиях» — основах мироздания, атомы которых он мыслил в виде правильных тел. (Подробнее это учение Платона мы рассмотрим в п. 4.3.) С тех пор правильные многогранники часто называют телами Платона.

Правильные многогранники на протяжении всей истории человечества не переставали восхищать пытливые умы симметрией, мудростью и совершенством своих форм. Леонардо да Винчи любил мастерить каркасы правильных тел и преподносить их в дар знатным особам, возможно, пытаясь таким образом приобщить сильных мира сего к философским размышлениям о красоте вечных истин (рис. 47).

Рис. 47. Рисунки деревянных моделей додекаэдра и икосаэдра, выполненные Леонардо да Винчи для книги его друга Луки Пачоли «О божественной пропорции». Венеция. 1509 г.

Но на пяти правильных телах история многогранников не остановилась. Вслед за правильными телами Платона были открыты полуправильные тела Архимеда, грани которых составлены из правильных равных многоугольников нескольких видов, причем в каждой вершине сходится одно и то же число одинаковых граней в одинаковом порядке и многогранные углы при вершинах равны. Заметим, что тела Архимеда могут быть получены из соответствующих тел Платона снятием равных фасок. Тел Архимеда всего 13. Любопытно, что во второй половине XX в. было обнаружено еще одно тело Архимеда — псевдоромбокубооктаэдр, которое не может быть получено путем однотипных усечений тела Платона и поэтому в течение 2000 лет оставалось незамеченным.

В XVII в. Кеплером и в XVIII в. Пуансо были найдены различные формы звездчатых невыпуклых многогранников, получаемых продолжением граней правильного или полуправильного тела до самопересечения. Простейшее тело такого типа — «звезда Кеплера» — было обнаружено Кеплером в 1619 г. и получается продолжением граней октаэдра (рис. 48). Впрочем, это же тело можно представить и как пересечение двух тетраэдров. Звездчатые многогранники поражают воображение красотой и причудливым разнообразием своих форм (рис. 49). Тем, кого вдохновит эта форма, мы рекомендуем книгу М. Венниджера «Модели многогранников» (М.: Мир, 1974), познакомившись с которой можно на свой вкус выбрать и сделать самый экзотический звездчатый многогранник.

Рис. 48. Рис. 49. Седьмая звездчатая форма тела Архимеда — икосододекаэдр.

И все-таки знакомство с многогранниками мы советуем начать с «Начал» Евклида, ибо, как сказал Альберт Эйнштейн, «Тот не рожден для теоретических исследований, кто в молодости не восхищался этим творением».

Источник