Что такое правильные неправильные дроби
Правильные и неправильные дроби
Обыкновенные дроби делятся на правильные и неправильные.
Правильные дроби
Правильная дробь — это обыкновенная дробь, у которой числитель меньше знаменателя.
Чтобы узнать является ли дробь правильной, надо сравнить её члены между собой. Члены дроби сравниваются в соответствии с правилом сравнения натуральных чисел.
Пример. Рассмотрим дробь:
у которой 7 — это числитель, а 8 — знаменатель. Сравним числитель со знаменателем:
7 Пример 1. Рассмотрим дробь:
у которой 8 — это числитель, а 7 — знаменатель. Сравним числитель со знаменателем:
Так как числитель больше знаменателя, значит данная дробь является неправильной.
Пример 2. Рассмотрим дробь:
Сравним числитель со знаменателем:
Так как числитель равен знаменателю, значит данная дробь является неправильной.
Любая неправильная дробь больше единицы или равна ей:
Обратите внимание, что любое натуральное число можно представить в виде неправильной дроби, следующим образом:
Дробь с числителем p и знаменателем 1 – это другая форма записи натурального числа p: 
Число 0 принято считать равным дроби вида 
Любую неправильную дробь, у которой числитель больше знаменателя можно представить в виде смешанного числа.
Сравнение правильных и неправильных дробей
Любая неправильная обыкновенная дробь больше правильной, так как правильная дробь всегда меньше единицы, а неправильная больше единицы или равна ей.
Правильные и неправильные дроби.
Виды дробей.
Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)
Делятся дроби на два вида правильные дроби и неправильные дроби.
В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)
В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Единицу мы можем представить как дробь \(1 = \frac<3><3>\)
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)
Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.
Дроби
Что такое дробь
Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.
Дробная черта равносильна знаку деления. То есть \(4:6=\frac46\) (четыре шестых), \(7:2=\frac72\) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Знаменатель дроби не может быть нулем.
Основные свойства дробей
Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).
Существует два вида дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: \(\frac <39>
Правильные дроби
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого: \( \frac25
Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.
Смешанные дроби
Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.
Смешанное число — это число, содержащее целую и дробную часть.
Для составления смешанной дроби необходимо:
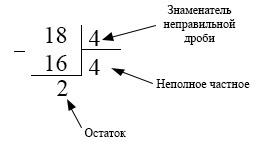
Записать неправильную дробь \(\frac<18>4\) в виде смешанной.
Тогда искомая смешанная дробь \(\frac<18>4=4\frac24.\) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:
Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.
Смешанное число \(6\frac25\) записать в виде неправильной дроби.
Как перевести правильную дробь в неправильную
Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.
Любое натуральное число можно представить в виде неправильной дроби: \(2=\frac21.\)
Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: \(p=\frac p1.\)
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби \(\frac ab\) и \(\frac cd\) к общему знаменателю, необходимо:
Сравнение
Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.
\(\frac34>\frac13,\) поскольку \(\frac9<12>>\frac4<12>.\)
Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.
К примеру, \(8\frac16>5\frac23.\)
Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: \(5\frac23>5\frac13.\)
Сложение и вычитание
Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.
При сложении смешанных чисел целые и дробные части складываются отдельно.
Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.
Умножение и деление
Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.
\(\frac ab\cdot\frac cd=\frac
Умножить дробь \(\frac35\) на \(\frac23.\)
При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде \(p=\frac p1.\)
\(\frac ab\cdot p=\frac ab\cdot\frac p1=\frac
Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.
Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.
\(\frac ab:\frac cd=\frac ab\cdot\frac dc=\frac
Поделить дробь \(\frac34\) на \(\frac23.\)
При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби.
Дроби обыкновенные правильные и неправильные, смешанные и составные.
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида 
Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).
или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:
Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:
Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:
Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.
Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).
К подобному виду обычно и приводят смешанные дроби.
Составные дроби.
Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:



Правильные и неправильные дроби
Вы будете перенаправлены на Автор24
Обыкновенные дроби делятся на \textit <правильные>и \textit <неправильные>дроби. Такое разделение основано на сравнении числителя и знаменателя.
Правильные дроби
Существует определение правильной дроби, которое базируется на сравнении дроби с единицей.
Неправильные дроби
Дадим определение неправильной дроби, которое базируется на ее сравнении с единицей.
Готовые работы на аналогичную тему
Рассмотрим более подробно понятие неправильной дроби.
Рассмотрим далее неправильные дроби:
При работе с неправильными дробями прослеживается тесная связь между ними и смешанными числами.
Решение.
Разделим числитель на знаменатель с остатком:
Чтобы записать смешанное число в виде неправильной дроби, необходимо знаменатель умножить на целую часть числа, к произведению, которое получилось, прибавить числитель дробной части и записать полученную сумму в числитель дроби. Знаменатель неправильной дроби будет равен знаменателю дробной части смешанного числа.
Решение.
Сложение смешанного числа и правильной дроби
Решение.
Воспользуемся формулой сложения смешанного числа и правильной дроби:
Сложение смешанного числа и неправильной дроби
Сложение неправильной дроби и смешанного числа сводят к сложению двух смешанных чисел, для чего достаточно выделить целую часть из неправильной дроби.
Решение.
Далее сложение смешанного числа и неправильной дроби сводится к сложению двух смешанных чисел:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 10 06 2021