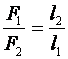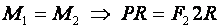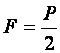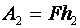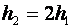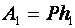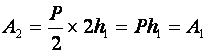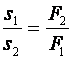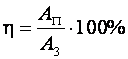Что такое правило механизмов
Что такое правило механизмов
Код ОГЭ 1.19. Простые механизмы. «Золотое правило механики». Рычаг. Момент силы. Условие равновесия рычага. Подвижный и неподвижный блоки. КПД простых механизмов.
Простыми механизмами называются устройства, позволяющие совершить работу без применения источников немеханической энергии. С их помощью можно получить выигрыш в силе или изменить направление её действия.
Золотое правило механики : При отсутствии трения выигрыш в силе равен проигрышу в расстоянии (простые механизмы не дают выигрыша в работе).
Коэффициент полезного действия (КПД, ɳ) – физическая величина, равная отношению полезной работы (мощности, энергии) ко всей затраченной работе (мощности, энергии), выраженному в процентах: 
Виды простых механизмов
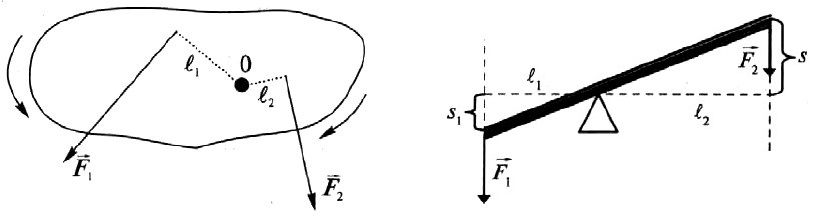
Условие равновесия рычага: Суммарный момент сил, вращающих рычаг по часовой стрелке, равен суммарному моменту сил, вращающих рычаг против часовой стрелки.
Момент силы М ([М] = Н • м) – физическая величина, равная произведению модуля силы на плечо: М = Fl.
Плечо силы (l или d) относительно указанной точки – кратчайшее расстояние от точки до линии действия силы, то есть длина перпендикуляра, опущенного из точки на линию действия силы.
Линия действия силы – прямая линия, на которой лежит вектор силы.
Выигрыш в силе: 
Конспект урока по физике в 9 классе «Простые механизмы. Золотое правило механики».
Золотое правило механики

Всего получено оценок: 733.
Всего получено оценок: 733.
Благодаря простым механизмам было сформулировано «золотое правило» механики. Оказалось, что все перемещения в простых механизмах имеют определенную связь с силами, которые развивает машина. Что же называют «золотым правилом механики»?
Простые механизмы
На протяжении многих столетий человек использует для совершения механической работы различные предметы и приспособления – простые механизмы. Различают следующие простые механизмы: рычаг, блок, ворот, винт, наклонная плоскость.
Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры. Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
А вот как сформулировал постулаты о рычаге сам Архимед:
1. Равные веса, находящиеся на равных расстояниях (от точки опоры), находятся в равновесии, а равные веса, находящиеся на неравных расстояниях, не находятся в равновесии, но перевес происходит в сторону того веса, который находится на большем расстоянии.
2. Если два веса, находясь на определенном расстоянии, уравновешивают друг друга и если к одному из этих весов что-нибудь прибавить, то веса уже не будут уравновешивать друг друга, но наклонятся к тому весу, который увеличили.
3. Если подобным же образом отнять что-либо от одного из весов, то весы не останутся в равновесии, но отклонятся к тому, от которого не отнимали.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелки, равен моменту силы, вращающему его против часовой стрелки.
Блок представляет собой колесо с желобом, которое укреплено в обойме.

Неподвижным блоком называют такой блок, ось которого закреплена и при подъеме грузов не поднимается и не опускается. Неподвижный блок можно рассматривать как равноплечный рычаг, у которого плечи сил равны радиусу колеса. Такой блок не дает выигрыша в силе, но позволяет менять направление действия силы.
У подвижного блока ось опускается и поднимается вместе с грузом, он позволяет получать выигрыш в силе.
«Золотое правило механики»
Перемещения, пройденные точками приложения сил на рычаге, обратно пропорциональны приложенным силам – это и есть «золотое правило» механики, которое можно выразить следующей формулой:
Пользуясь правилом пропорции, получаем из последнего выражения равенство работ, совершенных плечами рычага:
Золотое правило механики гласит: не один механизм не дает выигрыша в работе. Во сколько раз мы выигрываем в силе во столько же раз мы проигрываем в расстоянии.

Что мы узнали?
Простые механизмы известны со времен Архимеда. В данной статье даны определения таких механизмов, как рычаг и блок. Используя простые механизмы, выигрываем в одном, например в силе, зато проигрываем в другом – в расстоянии.
Блоки. Золотое правило механики
Урок 39. Физика 7 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Блоки. Золотое правило механики»
Блоки. Золотое правило механики
«Мыслящий ум не чувствует себя счастливым,
пока ему не удастся связать воедино разрозненные
факты, им наблюдаемые»
Данная тема посвящена изучению блоков. А также рассмотрению «Золотого правила механики».
В прошлых темах говорилось о простых механизмах, таких как рычаг. Рычаг — это любое твердое тело, которое может поворачиваться относительно неподвижной опоры или оси.
Рычаги бывают двух видов – рычаг первого и рычаг второго рода. Рычаг первого рода — это рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Рычаг второго рода — это рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу.
Вывели условие равновесия рычага, согласно которому, рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.
Рассмотрели момент силы — физическую величину, равную произведению модуля силы, вращающей тело, на ее плечо. И сформулировали условие равновесия рычага через правило моментов, согласно которому, рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.
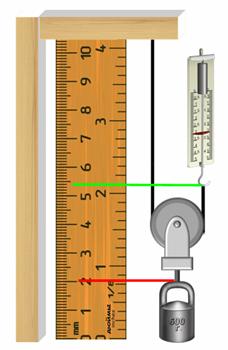
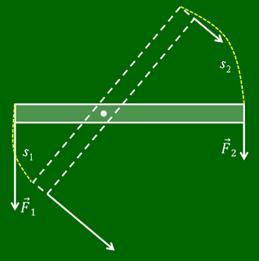
Однако, помимо рычагов, нередко для подъема грузов используется и простой блок или система блоков. Особенно часто применяются блоки на стройплощадках, в портах и на складах. Любой блок представляет собой колесо с жёлобом, укрепленное в обойме. По жёлобу блока пропускают веревку, трос или цепь.
А какие бывают блоки? И как они преобразуют силу?
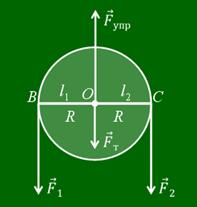
Если ось блока закреплена и при подъеме грузов она не опускается и не поднимается, то блок называется неподвижным. Такой блок можно рассматривать как равноплечный рычаг, у которого плечи сил равны радиусу колеса. Дает ли такой блок выигрыш в силе? Поставим опыт. Возьмем груз весом 3 Н и подвесим к одному концу перекинутой через блок нити, а к другому прикрепим динамометр. При равномерном подъеме груза динамометр покажет силу, равную весу груза, т.е. 3 Н. Изобразим схематически силы, действующие на блок.
Это сила упругости нити, равная весу груза, сила упругости нити, равная приложенной к динамометру силе, сила тяжести, действующая на блок и сила упругости оси блока. Как видно из рисунка, плечи сил тяжести и упругости блока равны нулю. Значит и их моменты относительно оси равны нулю. Плечи сил упругости нити один и два равны между собой как радиусы блока. В состоянии равновесия блока моменты сил F1 и F2 должны быть равны. А раз равны моменты этих сил, то и сами силы равны между собой. Иными словами, прилагаемая сила равна весу груза. Таким образом, неподвижный блок не дает выигрыша в силе, а лишь изменяет ее направление.
Зачем применять неподвижный блок, если выигрыша в силе нет? Ведь с таким же успехом для подъема груза можно было бы использовать любую перекладин. Можно, но проигрышно, так как придется преодолевать силу трения скольжения веревки по перекладине, которая значительно больше силы трения качения в подшипнике блока.
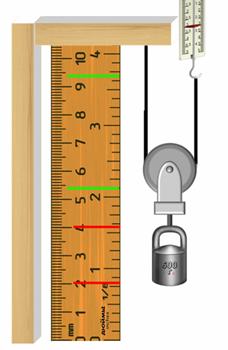
А может ли все-таки блок дать выигрыш в силе? Рассмотрим другой вид блока — подвижный блок. Подвижным называется блок, ось вращения которого при подъеме груза движется вместе с грузом.
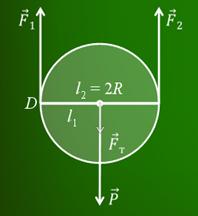
Подвесим к такому блоку груз весом 6 Н. Один конец перекинутой через блок нити закрепим, а за другой будем равномерно поднимать груз при помощи динамометра. Динамометр показывает, что прилагаемая к концу веревки сила равна 3 Н, т. е. в два раза меньше веса груза. Следовательно, подвижный блок дает выигрыш в силе примерно в 2 раза. Почему?
На блок действуют вес груза, силы упругости нити, которые равны между собой, и сила тяжести блока. При этом, чаще всего, силой тяжести блока пренебрегают, так как она, как правило, намного меньше веса груза. При движении груза подвижный блок поворачивается относительно точки D. Следовательно, подвижный блок — это рычаг второго рода. Запишем условие равновесия для него через правило моментов. Из рисунка видно, что плечо веса груза равно радиусу блока, а плечо второй силы — двум радиусам блока.
С учетом того, что сила F2 равна силе F, прилагаемой к концу веревки, и используя основное свойство пропорции, получим
Таким образом, можно сделать вывод о том, что подвижный блок дает выигрыш в силе в два раза.
Теперь можно сделать главный вывод о том, что при использования простых механизмов, мы можем получить выигрыш в силе.
Встает логичный вопрос: А можно ли с помощью простого механизма получить выигрыш в работе? Если прилагаемая сила меньше веса груза, то будет ли совершенная ею работа меньше работы по подъему груза без использования механизма?
Поставим опыт. Будем поднимать равномерно груз на некоторую высоту с помощью подвижного блока (силой тяжести блока и силой трения пренебрегаем).
Работа силы, приложенной к нити, равна произведению приложенной к нити силы и высоты подъема ее точки приложения.
Как видно из рисунка, высота подъема точки приложения силы в два раза больше высоты подъема груза. Работа по подъему груза равна по модулю произведению веса груза и высоты подъема груза.
Теперь сравним две работы. При этом учтем, что сила, приложенная к концу веревки примерно в два раза меньше веса груза.
Принимая этот факт во внимание, получим, что работа по подъему груза равна работе приложенной к нити силы.
Таким образом, использование подвижного блока не дает выигрыша в работе. Так как, имеется выигрыш в 2 раза в силе и проигрыш в 2 раза в пути.
Аналогично можно подойти к рассмотрению рычага. Для этого на рычаге уравновешиваются 2 разные по модулю силы, и рычаг приводится в движение.
Если измерить расстояния, пройденные большей и меньшей силами, и модули этих сил, то получим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам.
Таким образом, как и в случае с подвижным блоком, можем заключить, что действуя на длинное плечо рычага, выигрываем в силе, но при этом во столько же раз проигрываем в пути. Так как произведение силы на путь есть работа, то и в этом случае, выигрыш в работе не получается.
Как показала многовековая практика, ни один механизм не дает выигрыша в работе. Это утверждение получило название «Золотое правило механики». Если с помощью какого-либо простого механизма выигрываем в силе, то во столько же раз проигрываем в пути.
Можно ли при сравнении работ ставить между ними строгое равенство? Ведь делая тот или иной вывод, вводилось условие о том, что силой тяжести, действующей на блок, и силой трения в блоке можно пренебречь? Однако трение существует. Оно присутствует во всех механизмах. И сила тяжести, которая действует на сам блок, пусть даже и небольшая, тоже есть. Даже если не происходит подъема простого механизма или его частей (как в случае неподвижного блока), необходимо прилагать дополнительную силу на приведение его в движение, т. е. на преодоление инертности механизма. Поэтому прилагаемая к механизму сила должна реально совершать большую работу, чем полезная работа по подъему груза.
Работа силы, приложенной к механизму, называется затраченной или полной работой. А полезной является работа по поднятию только самого груза.
Если рассмотреть любой механизм, то полезная работа всегда составляет лишь некоторую часть полной работы. Обозначим полезную работу как AП, а затраченную — A3. Отношение полезной работы, к работе затраченной, называется коэффициентом полезного действия механизма (сокращенно КПД).
Коэффициент полезного действия обозначается маленькой греческой буквой h (эта) и, чаще всего, выражается в процентах. Так как полезная работа всегда меньше совершенной, то коэффициент полезного действия механизма всегда меньше 100%.
Задача 1. Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 50 кг с помощью подвижного блока? На какую высоту будет поднят мешок при совершении этой силой работы в 2500 Дж?
Задача 2. Плита массой 120 кг была равномерно поднята с помощью подвижного блока на высоту 16 м за промежуток времени, равный 40 с. Считая коэффициент полезного действия равным 80%, а массу блока — 10 кг, определите полную работу и развиваемую мощность.
– Блок — это одна из разновидностей рычага, который представляет собой колесо с желобом, укрепленное в обойме. Различают подвижный и неподвижный блоки.
– Неподвижный блок — это блок, ось вращения которого закреплена и при подъеме грузов она не поднимается и не опускается.
– Подвижный блок — это блок, ось вращения которого поднимается и опускается вместе с грузом.
– Неподвижный блок не дает выигрыша в силе, а лишь меняет ее направление.
– Подвижный блок, если пренебречь трением и весом самого блока, дает выигрыш в силе в два раза.
– «Золотое правило механики», согласно которому во сколько раз выигрываем в силе, во столько же раз проигрываем в пути.
– Коэффициента полезного действия механизма показывает, какую часть от совершенной прилагаемой силой работы составляет полезная работа.
– Полезная работа всегда меньше совершенной. Коэффициент полезного действия любого механизма меньше 100%.
Простые механизмы. «Золотое правило» механики
п.1. Виды простых механизмов
По традиции, сложившейся ещё со времен Возрождения, к простым механизмам относятся:
Примеры физических систем в механике
п.2. Принцип действия рычага
Подробно рычаги и условия равновесия были рассмотрены в §26 данного справочника.
В этом разделе мы рассмотрим принцип работы рычага с точки зрения закона сохранения энергии.
Пусть действие приложенной силы \(F_1\) приводит к перемещению \(h_1\) левого плеча вниз.
Работа приложенной силы равна \(A_1=F_1h_1\).
Тогда правое плечо при этом переместится вверх на расстояние \(h_2\).
Получаем, что \(F_1h_1=F_2h_2\).
Что соответствует результату, полученному ранее.
п.3. «Золотое правило» механики
 | Архимеду приписывают следующую фразу: «Дайте мне точку опоры, и я переверну Землю». |
Попробуем для начала хотя бы сдвинуть Землю на 1 микрон с орбиты, \(h_2=1\ \text<мкм>=10^<-6>\ \text<м>\). Это послужит хорошей иллюстрацией «золотого ПРАВИЛО» механики.
Расстояние от Солнца до Земли – 1 астрономическая единица – это «всего лишь» 150 миллионов километров:\(1\ \text<а.е.>\approx 1,5\cdot 10^<11>\ \text<(м)>\).
Значит, если на одной стороне рычага мы сдвигаем Землю на 1 микрон, то на другой стороне – прикладывая весь свой вес – должны преодолеть расстояние в полторы Солнечных системы. Вот что такое – «проигрыш в расстоянии».
п.4. Блоки и полиспасты
Блок — это колесо с желобом, по которому пропущена веревка или трос.
В технике используют неподвижные и подвижные блоки.
Подвижный блок даёт выигрыш в силе в 2 раза.
При этом получаем двойной проигрыш в расстоянии: чтобы поднять груз на высоту \(h\), нужно вытравить канат справа на длину \(2h\).
В реальных ситуациях выигрыш в силе при использовании подвижного блока получается меньшим, т.к. часть работы уходит на подъем самой веревки и блока (они тоже имеют вес) и преодоление трения.
На практике используют комбинации из неподвижных и подвижных блоков – полиспасты.
Они позволяют получить выигрыш в силе и менять её направление.
Чем больше в полиспасте подвижных блоков, тем большим будет выигрыш в силе.
Характеристики полиспастов представлены в таблице.
| № | К-во неподвижных блоков | К-во подвижных блоков | Изменение направления силы, раз | Выигрыш в силе, раз | Проигрыш в расстоянии, раз |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 3 | 3 |
| 4 | 1 | 3 | 1 | 4 | 4 |
| 5 | 1 | 4 | 1 | 5 | 5 |
| 6 | 1 | 5 | 1 | 6 | 6 |
п.5. «Золотое правило» механики для гидравлического пресса
Подробней о гидравлическом прессе – см. §30 данного справочника.
Работы малого и большого поршня равны.
Таким образом, «золотое правило» для гидравлического пресса также выполняется.
Гидравлический пресс не дает выигрыша в работе.
п.6. «Золотое правило» механики для наклонной плоскости
В любом случае тело, оказавшись в точке B, приобретает потенциальную энергию \begin
Получаем \begin
Наклонная плоскость не дает выигрыша в работе.
Выигрыш в силе компенсируется проигрышем в расстоянии.
Выигрыш в силе равен отношению длины наклонной плоскости к высоте.
Например, из пяти наклонных плоскостей, представленных на рисунке, наибольший выигрыш в силе даст плоскость 5, т.к. у нее отношение \(\frac Lh\) максимально (угол наклона минимален).
В реальности, если учесть силу трения, этот выигрыш уменьшается, т.к. с уменьшением угла наклона сила трения растет.
п.7. Задачи
Задача 1. Груз весом 200 Н равномерно поднимают по наклонной плоскости на высоту 5 м, прикладывая силу 100 Н. Найдите длину наклонной плоскости. Трением можно пренебречь.
Работы при подъеме тела вверх и при перемещении вдоль наклонной плоскости равны: \(A=Ph=FL\). Получаем \begin
Задача 2. При штамповке детали больший поршень гидравлического пресса поднялся на 1 см, а меньший поршень опустился на 20 см. Какая сила действовала на деталь, если на малый поршень действовала сила 500 Н.
Работы по перемещению поршней равны: \begin
Задача 3. К концам рычага длиной 1 м подвешены грузы массой 8 кг и 12 кг. На каком расстоянии от середины рычага должна быть точка опоры, чтобы рычаг находился в равновесии? Ответ запишите в сантиметрах.
Плечо для груза 1: \begin
Задача 4. Если груз лежит на левой чашке неравноплечих весов, его уравновешивают гири массой \(m_1=2\ \text<кг>\) на правой чашке. Если же груз положить на правую чашку, его уравновесит только одна гиря массой \(m_2=0,5\ \text<кг>\) на левой чашке. Какова масса \(m\) груза? Во сколько раз одно плечо весов длиннее другого?
Пусть длина правого плеча \(L_1\), левого плеча – \(L_2\).
По условию задачи \begin
Ответ: 1 кг; левое плечо длиннее правого в 2 раза
Задача 5*. Прямолинейный кусок проволоки массой \(m=40\ \text<г>\) подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы груз надо подвесить в точке A, чтобы восстановить равновесие.
Пусть длина всей проволоки \(L\).
Тогда расстояние от центра тяжести проволоки слева до точки подвеса \(OK=L/4\), а расстояние от центра тяжести проволоки справа до точки подвеса \(OE=L/2\).
Груз массой \(M\) подвешен на расстоянии \(OA=L/2\).
Из ПРАВИЛА моментов получаем: \begin
Сокращаем на \(gL\) \begin
Задача 6*. Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м.
Какую силу, перпендикулярную балке и направленную вертикально вверх нужно приложить, чтобы приподнять балку за один из её краёв?