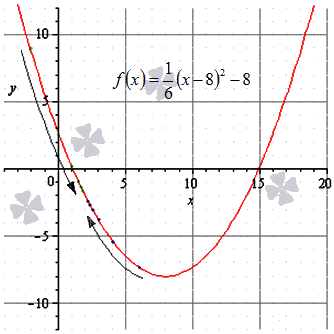
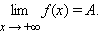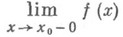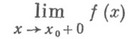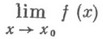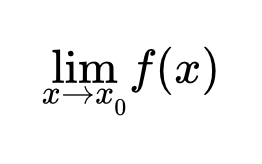Что такое предел слева и справа
Что такое предел слева и справа
Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.
Определения предела функции по Коши и по Гейне эквивалентны.
Так, функция имеет в точке бесконечный предел Часто различают пределы, равные +∞ и –∞. Так,
Если для каждого ε > 0 существует такое δ > 0, что для любого > δ выполняется неравенство 
Для вычисления пределов часто используют так называемые замечательные пределы :
Для доказательства первого предела используется неравенство
 , |
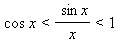верное для (неравенство следует из определения синуса при рассмотрении единичной окружности, а для доказательства неравенства необходимо нарисовать ось тангенсов). Для доказательства второго предела используются теорема о пределе монотонной функции и монотонная ограниченная последовательность
Функция α называется бесконечно малой при (здесь – конечное число или ∞), если Функция является бесконечно малой функцией в каждой точке. Примерами бесконечно малых (на бесконечности) функций являются зависимость силы тяжести от расстояния до притягивающего центра или зависимость скорости движения по параболической орбите от времени.
Предел функции: основные понятия и определения
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
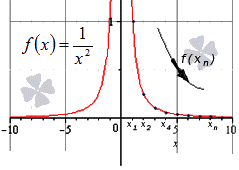
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Решение
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
Ответ: Верность данного в условии равенства подтверждена.
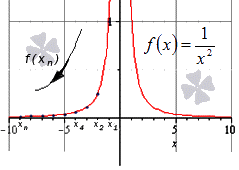
Решение
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Теперь сформулируем, что такое предел функции справа.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Решение
Значения функции в этой последовательности будут выглядеть так:
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
ОДНОСТОРОННИЙ ПРЕДЕЛ
(он не зависит от выбора 
), а предел по интервалу 
наз. пределом справа и обозначают
(он не зависит от выбора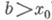 
). Если точка 
является предельной как слева, так и справа для множества определения функции f, то обычный предел
по проколотой окрестности точки х 0 (в этом случае его наз. также двусторонним, в отличие от односторонних пределов) существует тогда и только тогда, когда в точке х 0 существуют пределы слева и справа и они равны между собой.
Смотреть что такое «ОДНОСТОРОННИЙ ПРЕДЕЛ» в других словарях:
Односторонний предел — в математическом анализе предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).… … Википедия
Предел функции — x 1 0.841471 0.1 0.998334 0.01 0.999983 Хотя функция (sin x)/x в нуле не определена, когда x приближается к нулю, значение (sin x)/x становится сколь угодно близко к 1. Другими словами, предел функции (sin x)/x при x, стремящемся к … Википедия
Предел слева — Односторонний предел в математическом анализе предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом… … Википедия
Предел справа — Односторонний предел в математическом анализе предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом… … Википедия
ПРЕДЕЛ — одно из основных понятий математики, означающее, что какая то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек рому постоянному значению. Основным при определении П. является… … Математическая энциклопедия
Левосторонний предел — Односторонний предел в математическом анализе предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом… … Википедия
Правосторонний предел — Односторонний предел в математическом анализе предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом… … Википедия
Замечательный предел — Содержание 1 Первый замечательный предел 2 Второй замечательный предел 2.1 … Википедия
нижний доверительный предел — 3.4 нижний доверительный предел (lower confidence limit) sLCL, МПа: Величина, определяющая свойство рассматриваемого материала, представляющая собой 97,5 % нижнего доверительного предела предсказанной длительной гидростатической прочности при 20… … Словарь-справочник терминов нормативно-технической документации
нижний доверительный предел прогнозируемого гидростатического давления pLPL, МПа — 3.7 нижний доверительный предел прогнозируемого гидростатического давления pLPL, МПа: Величина с размерностью давления, представляющая собой 97,5 % ный (односторонний) нижний доверительный предел прогнозируемого гидростатического давления при… … Словарь-справочник терминов нормативно-технической документации
Предел функции – определения, теоремы и свойства
Определение предела функции
Первое определение предела функции по Гейне
С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.
См. «Универсальное определение предела функции по Гейне и по Коши».
Второе определение по Коши
Здесь a и x 0 также могут быть как конечными числами, так и бесконечно удаленными точками. С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.
Если в качестве множества взять левую или правую окрестность конечной точки, то получим определение предела по Коши слева или справа.
Теорема
Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство
Применяемые окрестности точек
Далее мы приводим формулировки определений предела функции по Коши для разных случаев, используя определения окрестностей с равноудаленными концами.
Конечные пределы функции в конечных точках
С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.
Конечные пределы функции в бесконечно удаленных точках
Аналогичным образом определяются пределы в бесконечно удаленных точках.
.
.
.
Бесконечные пределы функции
Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.
Свойства и теоремы предела функции
Основные свойства
Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.
Если на некоторой проколотой окрестности точки x 0 :
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то
.
Доказательства основных свойств приведены на странице
«Основные свойства предела функции».
Арифметические свойства предела функции
Доказательства арифметических свойств приведены на странице
«Арифметические свойства предела функции».
Критерий Коши существования предела функции
Предел сложной функции
Доказательство теоремы приводится на странице
«Предел и непрерывность сложной функции».
Бесконечно малые и бесконечно большие функции
Бесконечно малые функции
Доказательства свойств изложены в разделе
«Свойства бесконечно малых функций».
Бесконечно большие функции
Свойства бесконечно больших функций
Связь между бесконечно большими и бесконечно малыми функциями
Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.
Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».
Пределы монотонных функций
Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.
Аналогичная теорема для невозрастающей функции.
Доказательство теоремы изложено на странице
«Пределы монотонных функций».
Определение функции, верхней и нижней грани
Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.
Если это особо не оговорено, мы рассматриваем функции, области определения и множества значений которых принадлежат множеству действительных чисел.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Односторонние пределы
Односторонние пределы
Определение 3.4. Число А называется правым (левым) пределом функции 
в точке 
, если для любой последовательности 
, сходящейся к , элементы которой больше (меньше) , соответствующая последовательность значений функции 
сходится к А при 
.
Таким образом, определение правого предела:
определение левого предела:
Предел справа обозначается 
, предел слева — 
.
Теорема 3.2*. Функция 
имеет предел в точке тогда и только тогда, когда в этой точке существуют правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции в точке .
Пример 3.3.
Найти односторонние пределы функции 
в х точке 
.
Решение:
Вывод. Так как односторонние пределы функции 
в точке 
существуют, но не равны между собой, то данная функция не имеет предела в этой точке.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института