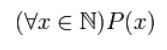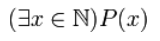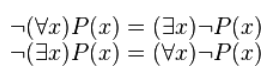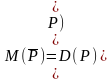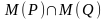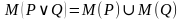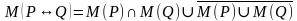Что такое предикат в математике дискретной

Предикат

Что такое предикат

Предикат (с латинского praedicatum означает «заявленное, упомянутое, сказанное») — понятие в логике, которым называют утверждение, высказанное о том или ином субъекте. Субъект высказывания — это та вещь или явление, о котором или которой делается утверждение.

Одна из важнейших особенности логики предикатов в том, что все общие имена (такие, как «цветок», «деревня»), знаки свойств («розовый», «большая») и знаки отношений («красивее», «роднее») рассматриваются как относящиеся к одной категории знаков: категории предикаторов (иначе говоря, предметно-истинных функторов).

Предикаторы, в свою очередь, показывают функции, у которых вероятные аргументы — это универсальные в рассмотрении объекты, а значения — истинные оценки. В классической логике они называются «истина» и «ложь». К примеру, возьмем предикатор «человек», который представляет функцию, определяемую как истина каждым отдельным человеком, а каждым отличным от человека существом — как ложь.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другой пример : функция, которая соответствует предикатору «больше», сопоставляет истину каждой паре объектов или субъектов, один из которых больше. Например, такая пара, как «слон, мышь». Но всем остальным парам, по типу «мышь, слон» и «мышь, мышь», такая функци будет сопоставлять оценку «ложь».

Предикаторы могут быть:

Логические операции над предикатами

Так как предикаты принимают два значения, «истина» и «ложь» (1 и 0), к ним можно применить все операции алгебры логики.

Представим, что в неком множестве N определены два предиката P(x) и Q(x). Рассмотрим все операции с ними по-отдельности.

Область истины в этом случае — объединение областей истинности обоих утверждений.

Область истины здесь — дополнение множества истинности утверждения P(x) до множества N, иначе говоря \(I_overline

=N\I_P=CI_P.\)

Кванторные операции над предикатами

Прежде чем изучить квантовые операции, нужно разобраться, что из себя представляет сам квантор.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание.

Кванторы впервые были определены немецким математиком Готлобом Фреге. Он упомянул их в своей работе «Begriffsschrift» («Исчисление понятий», 1879 года). Однако сам термин был изобретен английским логиком Чарльзом Пирсом в 1885 году. Вместе со словом «квантор» он ввел также и термин «квантификация», который означает измерение качеств признаков.

Обозначение кванторов

Символическое обозначение кванторов придумал итальянский математик Дж. Пеано в 90-е годы XIX века. Выглядят эти символы так:

\(\forall\) — «для любого», «для каждого», «для всех»;

\(\exists\) — «существует», «найдётся».

! – «единственный»;

: – «такой, что»;

| – «такой, что».

Знак «:» обычно используется в формулировках определений или теорем, которые записываются с помощью кванторов. Знак «|» применяется в определениях множеств.

Виды кванторов

Квантор общности \(\forall\)

Оно истинно только в том случае, когда \(P(x)\) — тождественно истинен. В ином случае данное высказывание ложно.

Оно истинно только в том случае, когда одноместный предикат \(P(x, a_2, …, a_n)\) на множестве \(N_1\) тождественно истинен. В противном случае оно ложно.

Квантор существования \( \exists\)

Примеры применения

Использование предикатов

Использование кванторов

Пусть предикат «x кратно 5». Тогда с помощью квантора общности можно записать ложные высказывания:

В этом случае решение будет выглядеть так:

Чтобы обозначить истинные высказывания, используем квантор существования:

В записи оно будет выглядеть так:

На множестве x простых чисел существует предикат: «Простое число является нечетным». Если мы поставим перед предикатом слово «любое», то получим ложное высказывание «Любое простое число является нечетным». Если мы поставим перед предикатом слово «существует», то получим истинное высказывание «Существует простое число, которое является нечетным».

Так, предикат можно превратить в высказывание, если поставить перед ним квантор.

Источник

Дискретная математика — предикатная логика

Логика предикатов имеет дело с предикатами, которые являются предложениями, содержащими переменные.

Предикатная логика — определение

Предикат — это выражение одной или нескольких переменных, определенных в некоторой конкретной области. Предикат с переменными можно сделать предложением, либо присвоив значение переменной, либо определив ее количественно.

Ниже приведены некоторые примеры предикатов:

Хорошо сформированная формула

Хорошо сформированная формула (wff) — это предикат, содержащий любое из следующего:

Все пропозициональные константы и пропозициональные переменные являются wffs

Если x — переменная, а Y — wff, то f o r a l l x Y и с у щ е с т в у ю щ и е x Y также являются wff

Истинное значение и ложные значения являются wffs

Каждая атомная формула является WFF

Все соединения, соединяющие wffs, являются wffs

Все пропозициональные константы и пропозициональные переменные являются wffs

Если x — переменная, а Y — wff, то f o r a l l x Y и с у щ е с т в у ю щ и е x Y также являются wff

Истинное значение и ложные значения являются wffs

Каждая атомная формула является WFF

Все соединения, соединяющие wffs, являются wffs

Кванторы

Переменная предикатов определяется количественно квантификаторами. Существует два типа квантификаторов в логике предикатов — универсальный квантификатор и экзистенциальный квантификатор.

Универсальный квантификатор

f o r a l l x P ( x ) читается как для каждого значения x, P (x) верно.

Экзистенциальный квантификатор

с у щ е с т в у е т x P ( x ) читается как для некоторых значений x, P (x) верно.

Вложенные квантификаторы

Если мы используем квантификатор, который появляется в области действия другого квантификатора, он называется вложенным квантификатором.

Источник

Предикаты и кванторы

Вы будете перенаправлены на Автор24

Понятие предиката

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Примеры предикатов

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Готовые работы на аналогичную тему

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Чаще всего используют кванторы:

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

С помощью квантора всеобщности можно записать следующие ложные высказывания:

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

Запись будет иметь вид:

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

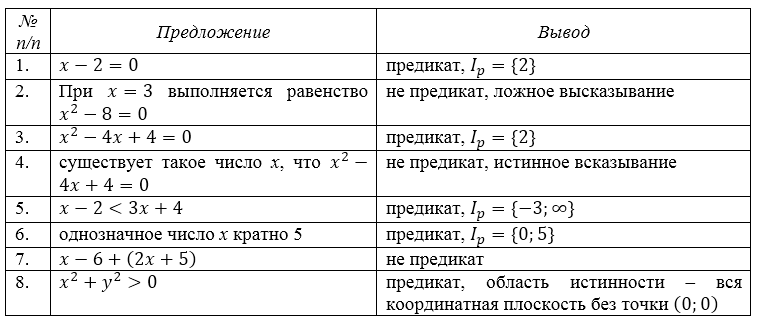
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 07 04 2016

Источник

Лекция 3. Логика предикатов. Логические операции над предикатами

3.1. Понятие предиката

«Предикат» с английского переводится как сказуемое. Формально предикатом называется функция, аргументами которой могут быть произвольные объекты из некоторого множества, а значения функции «истина» или «ложь». Предикат можно рассматривать как расширение понятия высказывания.

Средства, предоставляемые логикой высказываний, оказываются недостаточными для анализа многих математи­ческих рассуждений. В алгебре логики не рассматриваются ни структура высказываний, ни, тем более, их содержание. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.

3.2. Логика предикатов

Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно может играть и роль дополнения) и предикат(буквально – сказуемое, хотя оно может играть и роль определения).

Субъект – это то, о чем что-то утверждается в высказывании, а предикат – это то, что утверждается о субъекте.

Логи­ка предикатов – это расширение логики высказываний за счет использова­ния предикатов в роли логических функций.

Например, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».

Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму «х – простое число». При одних значениях х (например, х = 13, х = 17) эта форма дает истинные высказывания, а при других значениях х (например, х = 10, х = 18) эта форма дает ложные высказывания.

Определение 1. Одноместным предикатом Р(х) называется всякая функция одного переменного, в которой аргумент x пробегает значения из некоторого мно­жества M, а функция при этом принимает одно из двух значений: истина или ложь.

Множество M, на котором задан предикат, называется областью определения предиката.

Множество , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).

Определение 2. Предикат Р(х), определённый на множестве M, называется тождественно истинным (тождественно ложным), если

Определение 3. Двухместным предикатом P(x, у) называется функция двух переменных х и у, определённая на множестве М=М₁×М₂ и принимающая значения из множества <1,0>.

В качестве примеров двухместных предикатов можно назвать предикаты: Q(x, у) – «х = у» предикат равенства, определённый на множестве R 2 =R×R; F(x, у) – «х || у» прямая х параллельна прямой у, определённый на множестве прямых, лежащих на данной плоскости.

Говорят, что предикат Р(х) является следствием предиката Q(х) , если ; и предикаты Р(х) и Q (х) равносильны , если .

Пример 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истин­ности:

Пусть на некотором множестве М определены два предиката Р(х) и Q(х).

Определение 4. Конъюнкциейдвух предикатов Р(х) и Q(х) называется новый предикат Р(х)&Q(х), который принимает значение «истина» при тех и только тех значениях , при которых каждый из предикатов Р(х) и Q(х) принимает значение «истина» и принимает значение «ложь» во всех остальных случаях. Очевидно, что областью истинности предиката Р(х)&Q(х) является общая часть областей истинности предикатов Р(х) и Q(х), т.е. пересечение .

Так, например, для предикатов Р(х): «х – четное число» и Q(х): « х кратно 3» конъюнкцией Р(х)&Q(х) является предикат «х – четное число и х кратно 3», то есть предикат «х делится на 6».

Определение 5. Дизъюнкцией двух предикатов Р(х) и Q(х) называется новый предикат , который принимает значение «ложь» при тех и только тех значе­ниях , при которых каждый из предикатов при­нимает значение «ложь» и принимает значение «исти­на» во всех остальных случаях. Ясно, что областью истинности предиката является объединение областей истинности предикатов Р(х) и Q(х), то есть объединение .

Определение 6. Отрицаниемпредиката Р(х) назы­вается новый предикат , который принимает значе­ние «истина» при всех значениях , при которых предикат Р(х) принимает значение «ложь», и принима­ет значение «ложь» при тех значениях , при кото­рых предикат Р(х) принимает значение «истина». Очевидно, что, .

Определение 7. Импликацией предикатов Р(х) и Q(х) называется новый предикат , который является ложным при тех и только тех значениях , при которых одновременно Р(х) принимает значение «истина», а Q(х) – значение «ложь» и принимает значе­ние «истина» во всех остальных случаях.

Ясно, что при выполнении логических операций над предикатами к ним применимы и равносильности алгеб­ры логики. Для детального изучения темы необходим курс «Дискретной математики».

Источник

Предикаты и операции над ними. Кванторы

Лекция по Дискретной математике предназначена для студентов 2 курса специальности 09.02.01 для самостоятельного изучения во время дистанционного обучения

Просмотр содержимого документа
«Предикаты и операции над ними. Кванторы»

Занятие 19. Тема «Предикаты и операции над ними. Кванторы»

Основные множества для предикатов

Операции над предикатами

Кванторы. Операции навешивания квантора

В дискретной математике, как и в математической теории, основными неопределяемыми понятиями являются понятия суждение, истина, ложь. Суждение не может быть одновременно истинным и ложным. Например, все предложения, которые произносит человек, являются суждениями. Суждение, зависящее от переменной величины, которое при подстановке значений переменного становится высказыванием, называют предикатом. Для описания внутренней логической структуры простых высказываний используется понятие предиката. Сегодня мы изучим основные понятия предикатов, рассмотрим операции, совершаемые с предикатами.

Определение. Предложения, содержащие переменные, истинность или ложность которого зависит от значения переменного, входящего в него, называется предикатом. Другими словами, это функция, заданная на определенном множестве. Обозначение Р(х), Р(х,у), …, Р(х1,х2, …,хn).

Пример. Высказывание А=«Волк – это хищник»

Предикат Р(х)=«х – это хищник». Истинность Р(х) будет зависеть от того, что поставить вместо х, т.е. если поставим х=Лиса, то получим истину, а если поставим х=Коза, то получим ложь.

Основные множества для предикатов

Считается, что с каждым предикатом задано множество, из которого выбирают значение переменных. Такое множество называют областью определения предиката. Обозначение D(P).

Подмножеством области определения предиката, на котором он принимает значение истинность, называется множеством истинности данного предиката. Обозначение М(Р). М(Р) 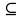D(P).

Операции над предикатами

Все операции будем рассматривать на примере Р(х)=«х-число, делящееся на 9», K(х)=«х-цифра». Для выполнения операций, нужно найти область определения предиката и множество истинности предиката и расписать эти множества как множество с перечислением элементов (с этого нужно начинать практическую), то есть

Для предиката Р(х)=«х-число, делящееся на 9»

Отрицанием предиката Р(х) называется новый предикат 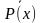, определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.

Пример. 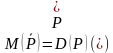=<1,2,3,4,5…95,96,97,98,…>\ <9,18,27,36,…,81,90,99,108,…>=<1,2,3,4,5,6,7,8,10,11,12,…,>то есть убрать из D(P) все числа, делящиеся на 9.

Конъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)⋀Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истины одновременно оба предиката P(x) и Q(x).

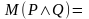
Пример. 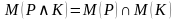=<9,18,27,36,…,81,90,99,108,…> <0,1,2,3,4,5,6,7,8,9>=

Дизъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)VQ(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истинен хотя бы один из предикатов P(x) и Q(x).

=<9,18,27,36,…,81,90,99,108,…> <0,1,2,3,4,5,6,7,8,9>=

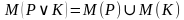
Импликацией двух предикатов Р(х) и Q(x) называется новый предикат Р(х) Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.

Пример. =<9,18,27,36,…,81,90,99,108,…>\ <0,1,2,3,4,5,6,7,8,9>=

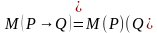
Эквиваленцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х) ↔ Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых либо оба предиката истины, либо оба предиката ложны.

=

= <9>,

=

=

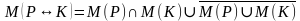
Кванторы. Операции навешивания квантора

Для количественных характеристик обычно используют понятия «все», «некоторые», «существуют» и др. В математике эти слова называются кванторами. От латинского слова quantum – сколько.

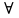
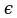
Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то ( х R)( х+3=8) – ложь. Читается это так «Для любого числа х из множества действительных чисел выполняется равенство х+3=8»-ложь

Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то ( х 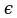R)( х+3=8) – истинно. Читается это так «Существует такое число х из множества действительных чисел, для которого выполняется равенство х+3=8»-истино.

Предикатная формула – это формула, содержащая знаки булевых операций и кванторов, то есть в формуле участвуют: символы предметных переменных, символы предикатов, логические символы и символы кванторов.

Задания для самостоятельной работы

Объяснить, почему следующие выражения имеют значение истина или ложь, описать выражения словами

Для следующих предложений выделить предикаты и для каждого из них указать область истинности:

однозначное число х кратно 3;

Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы

Запишите приведенные ниже утверждения в символической форме, введя предикаты. В случае необходимости укажите предметную область.

а) Некоторые машины умнее людей.

б) Любой играет в теннис лучше Фрэда.

в) Для каждого действует существует равное и противоположно направленное противодействие.

г) Каждый игрок в гольф, в конце концов, будет обыгран более сильным игроком

Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 5 п.5.3 стр.224, выполнить все задания.

Источник