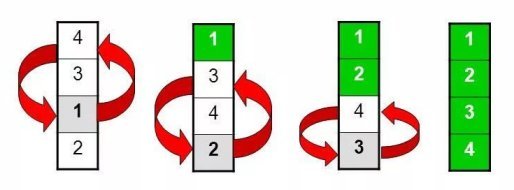
Что такое пузырьковая сортировка
Сортировка пузырьком
В процессе выполнения данного алгоритма элементы с большими значениями оказываются в конце списка, а элементы с меньшими значениями постепенно перемещаются по направлению к началу списка. Образно говоря, тяжелые элементы падают на дно, а легкие медленно всплывают подобно пузырькам воздуха.
В сортировке методом пузырька количество итераций внешнего цикла определяется длинной списка минус единица, так как когда второй элемент становится на свое место, то первый уже однозначно минимальный и находится на своем месте.
Количество итераций внутреннего цикла зависит от номера итерации внешнего цикла, так как конец списка уже отсортирован, и выполнять проход по этим элементам смысла нет.
Пусть имеется список [6, 12, 4, 3, 8].
За первую итерацию внешнего цикла число 12 переместится в конец. Для этого потребуется 4 сравнения во внутреннем цикле:
Результат: [6, 4, 3, 8, 12]
За вторую итерацию внешнего цикла число 8 переместиться на предпоследнее место. Для этого потребуется 3 сравнения:
Результат: [4, 3, 6, 8, 12]
На третьей итерации внешнего цикла исключаются два последних элемента. Количество итераций внутреннего цикла равно двум:
Результат: [3, 4, 6, 8, 12]
На четвертой итерации внешнего цикла осталось сравнить только первые два элемента, поэтому количество итераций внутреннего равно единице:
Результат: [3, 4, 6, 8, 12]
Реализация сортировки пузырьком с помощью циклов for
Пример выполнения кода:
С помощью циклов while
Функция сортировки пузырьком на Python
Сортировка пузырьком
Сортировка простыми обменами, сортиро́вка пузырько́м (англ. bubble sort ) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n²).
Алгоритм считается учебным и практически не применяется вне учебной литературы, вместо него на практике применяются более эффективные алгоритмы сортировки. В то же время метод сортировки обменами лежит в основе некоторых более совершенных алгоритмов, таких как шейкерная сортировка, пирамидальная сортировка и быстрая сортировка.
Содержание
Алгоритм
Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются N-1 раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу, очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим наибольшим элементом, а наименьший элемент перемещается на одну позицию к началу массива («всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма).
Псевдокод
Псевдокод улучшенного алгоритма (устойчивая реализация) с почти вдвое уменьшенным числом проходов.
На входе: массив A[N], состоящий из N элементов, с нумерацией от A[1] до A[N]
В улучшенном алгоритме количество повторов во внутреннем цикле уменьшается на 1 с каждой итерацией внешнего цикла.
Если нет функции обмена (SWAP A[I],A[I+1]), то её можно заменить тремя операторами присваивания:
Cложность: O(n·n), не уменьшается.
Наилучший случай (на вход подаётся уже отсортированный массив):
Особенность данного алгоритма заключается в следующем: после первого завершения внутреннего цикла максимальный элемент массива всегда находится на N-ой позиции. При втором проходе, следующий по значению максимальный элемент находится на N-1 месте. И так далее. Таким образом, на каждом следующем проходе число обрабатываемых элементов уменьшается на 1 и нет необходимости «обходить» весь массив от начала до конца каждый раз.
Так как подмассив из одного элемента не нуждается в сортировке, то для сортировки требуется делать не более N-1 итераций внешнего цикла. Поэтому в некоторых реализациях внешний цикл всегда выполняется ровно N-1 и не отслеживается, были или не были обмены на каждой итерации.
Введение индикатора (флажка F) действительно произошедших во внутреннем цикле обменов уменьшает число лишних проходов в случаях с частично отсортированными массивами на входе. Перед каждым проходом по внутреннему циклу флажок сбрасывается в 0, а после действительно произошедшего обмена устанавливается в 1. Если после выхода из внутреннего цикла флажок равен 0, то обменов не было, то есть массив отсортирован и можно досрочно выйти из программы сортировки.
Псевдокод ещё более улучшенного алгоритма с проверкой действительно произошедших обменов во внутреннем цикле.
Нв входе: массив A[N], состоящий из N элементов, с нумерацией от A[1] до A[N]
В случае досрочного выхода из сортировки в этом алгоритме делается один избыточный проход без обменов.
Наихудший случай (не улучшается):
Наилучший случай (улучшается):
Время сортировки 10000 коротких целых чисел на одном и том же программно-аппаратном комплексе (операция сравнения ≈3.4мкс, обмена ≈2.3мкс) сортировкой выбором составило ≈40сек., ещё более улучшенной сортировкой пузырьком ≈30сек, а быстрой сортировкой ≈0,027сек.
O(n·n) больше, чем O(n·log(n)) у сортировки слиянием, но при малых n разница не очень большая, а программный код очень прост, поэтому вполне допустимо применение сортировки пузырьком для множества задач с массивами малой размерности на простаивающих и малозагруженных машинах.
Алгоритм можно немного улучшить, сделав следующее:
В сортировке пузырьком, при каждом проходе по внутреннему циклу, можно добавить определение очередного минимального элемента и помещение его в начало массива, то есть объединить алгоритмы сортировки пузырьком и сортировки выбором, при этом число проходов по внутреннему циклу сокращается вдвое, но более чем вдвое увеличивается число сравнений и добавляется один обмен после каждого прохода по внутреннему циклу.
Псевдокод объединённого алгоритма сортировки пузырьком и сортировки выбором (устойчивая реализация):
Пример работы алгоритма
Возьмём массив с числами «5 1 4 2 8» и отсортируем значения по возрастанию, используя сортировку пузырьком. Выделены те элементы, которые сравниваются на данном этапе.
(5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами. (1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как 5 > 4 (1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как 5 > 2 (1 4 2 5 8) (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах (8 > 5), алгоритм не меняет их местами.
(1 4 2 5 8) (1 4 2 5 8) (1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как 4 > 2 (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8)
Теперь массив полностью отсортирован, но алгоритм не знает так ли это. Поэтому ему необходимо сделать полный проход и определить, что перестановок элементов не было.
(1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8) (1 2 4 5 8)
Теперь массив отсортирован и алгоритм может быть завершён.
Пузырьковая сортировка и бинарный поиск на PHP (обучение, эксперименты)
Введение
Хотел бы поделиться с сообществом своей реализацией пузырьковой сортировки и бинарного поиска. Проект сделал исключительно в учебных целях.
Когда меня раньше спрашивали на собеседовании об алгоритмах сортировки и реализации поиска по массивам данных — я терялся и считал, что для реализации подобных вещей надо быть как минимум талантливым отличником-олимпиадником, что это сложно-долго-малоизучено и т.п. 🙂 Так же я находил курсы, где за несколько недель (месяцев) предлагают научить всех желающих всему-всему по алгоритмам, сортировкам, криптографии. Но ведь сейчас есть Интернет, а в нем уже все выложено и известно? Остается только поднять и изучить нужные знания и практически реализовать и закрепить приобретенные знания.
Итак, приступим к реализации самих алгоритмов. Забегая вперед скажу, что статья состоит из трех логических частей: реализация алгоритмов, тестирование написанного кода (PHPUnit) и проведение нагрузочных тестов (базовые функции языка VS написанный код).
Т.е. как бы имитируется разработка некой системы (выполнение практической задачи) и прохождение по всем обязательным этапам (исходя из существующих на сейчас «стандартов» разработки).
Пузырьковая сортировка
НА Википедии и в профильных статьях довольно подробно и детально описаны все виды поиска. Сортировки анимированны, а на Ютубе есть видео с основными видами сортировок и наглядным отображением самого процесса упорядочивания массивов.
Перед началом написания кода я специально не вглядывался в код реализаций такой сортировки (для чистоты эксперимента), а лишь читал условия задачи. Начал писать код, подбросил тестовые данные, запустил скрипт в первый раз и смотрю на результат: массив отсортирован! В голове легкая паника! Что я сделал не так? Где ошибка? Ошибки нет — массив отсортирован верно.
Несколько строк кода — это и есть вся реализация пузырьковой сортировки?! Почему же я раньше считал, что это очень сложно и доступно не всем?
Бинарный поиск
Реализация бинарного поиска далась немного труднее. Несколько раз переписывал код, удалял и заново компоновал его. Часть времени пошла на подготовку тестовых данных и проверку различных ситуаций, при которых поиск должен работать корректно.
Но все успешно заработало. Единственное, что я не сейчас не знаю, что такое «переполнение целого при вычислении среднего индекса» 🙂
Тестирование кода
Код классов разнесен по отдельным файлам. Логично будет покрыть код юнит-тестами и, если мы внесем в реализацию какие-то изменения, иметь возможность быстро перепроверить работоспособность базового функционала.
При тестировании бинарного поиска были учтены следующие ситуации:
Пузырьковая сортировка тестируется достаточно просто — сравниваем результат, ожидаем корректный массив данных.
Нагрузочное тестирование
Сортировка, нагрузочные тесты
| PHP::sort() сек. | BubbleSort()->sort() сек. | |
|---|---|---|
| Массив из 100 элементов | 0.0000 | 0.0023 |
| Массив из 1000 элементов | 0.0002 | 0.2305 |
| Массив из 10000 элементов | 0.0031 | 23.1601 |
Поиск позиции элемента, нагрузочные тесты
| PHP::array_search() сек. | PHP::in_array() сек. | BinarySearch()->search() сек. | |
|---|---|---|---|
| Массив из 100 элементов | 0.000012 | 0.000004 | 0.000032 |
| Массив из 1000 элементов | 0.000003 | 0.000003 | 0.000026 |
| Массив из 10000 элементов | 0.000004 | 0.000003 | 0.000034 |
| Массив из 100000 элементов | 0.000005 | 0.000003 | 0.000046 |
| Массив из 1000000 элементов | 0.000003 | 0.000003 | 0.000005 |
Выводы по результатам тестирования:
Заключение
Буду рад, если подходы, мысли и идеи, которые я применял при написании этого кода пригодятся людям или послужат основой для обсуждения и нахождения более оптимальных решений.
Понимаю, что многие разработчики уже давно прошли подобные этапы взросления и становления как специалисты. Подобные задачи почти наверняка входят в университетскую программу лабораторных работ по программированию.
Весь код, приведенный в этой статье выложен на GitHub.
Готов выслушать ваши замечания и предложения.