Что такое расчетная длина
Расчетная длина стержня
Расчетная длина стержня
—
Расчетная длина l0 сжатых элементов является одним из главных параметров расчета на устойчивость. Для ее нахождения необходимо геометрическую длину стержня l умножить на коэффициент μ, зависящий от расчетной схемы. Так например, для шарнирно опертого стержня μ=1,0, а для стержня, жестко защемленного на обеих концах μ=0,5, т.е. гибкость такого стержня будет в два раза меньше первого, а для консольного стержня μ=2,0 — гибкость будет в два раза больше. Значения коэффициента μ для разных расчетных схем приведены на рисунках. Таким образом, расчетная схема определяет устойчивость стержней, что нельзя не учитывать при проектировании строительных конструкций.
Related posts:
10 комментариев к “Расчетная длина стержня”
Расчетная длина сжатых стержней стропильных ферм
Расчетные длины стержней ферм. Конструирование и расчет опорных узлов стропильных ферм. Расчет фермы с параллельными поясами длиной 12 м в SCAD. Часть 2-ая. Расчетная длина сжатых стержней стропильных ферм. Расчетные длины элементов фермы. УЗЛЫ ФЕРМ. Определение расчетной длины стержней. Расчетная длина сжатых стержней стропильных ферм. Железобетонные фермы. Как определяются расчетные длины элементов плоских ферм?
Определение расчетной длины стержней фермы
К определению расчетных длин элементов ферм Таким образом, расчетная длина пояса из плоскости фермы в общем случае равна расстоянию между точками, закрепленными от смещения. Элементами, закрепляющими пояс, могут служить кровельные панели, прогоны, связи и распорки. … стержня и меньше его расчетная длина. Влиянием сжатых стержней на защем-. ление можно пренебречь.
Определение расчетной длины стержней
Расчетная длина стержней решетки при выгибе их из плоскости фермы принимается равной расстоянию между геометрическими центрами узлов, так как фасонки очень гибки и рассматриваются как листовые шарниры. В трубчатых фермах с бесфасонными узлами расчетная длина раскоса, как в плоскости фермы, так и из нее, с учетом повышенной крутильной жесткости замкнутых сечений применятся равной 0,9.
РАСЧЕТНЫЕ ДЛИНЫ СТЕРЖНЕЙ — Строительные…
Расчетные длины стержней. Понятие расчетной длины применяется обычно при определении гибкости сжатых элементов, но в связи с тем, что в фермах определяют гибкости как сжатых, так и растянутых элементов, будем применять это понятие и к растянутым стержням. Расчетные длины, как и формы потери устойчивости, могут быть в плоскости и из плоскости фермы. Расчетные длины стержней в плоскости фермы 1Х…
Расчетные длины стержней
Расчетные сечения стержней. Смена типа конечного элемента (КЭ). Согласование осей объемных КЭ. … При задании расчетных длин элементов следует руководствоваться термином Относительно оси: Термин «относительно оси» означает плоскость, перпендикулярную оси. На рисунке плоскости, соответствующие осям, обозначены тем же цветом, что и оси, которым они соответствуют
9.6. Определение расчетной длины стержней
9.6. Определение расчетной длины стержней. В момент потери устойчивости сжатый стержень выпучивается, поворачивается вокруг центров соответствующих узлов и вследствие жесткости фасонок заставляет поворачиваться и изгибаться в плоскости фермы остальные стержни. Примыкающие стержни сопротивляются изгибу и повороту узла и препятствуют свободному изгибу стержня, теряющего устойчивость.
Расчетная длина стержня
Расчетная длина стержня. Расчетная длина стержня —. Расчетная длина l0 сжатых элементов является одним из главных параметров расчета на устойчивость. Для ее нахождения необходимо геометрическую длину стержня l умножить на коэффициент μ, зависящий от расчетной схемы. Так например, для шарнирно опертого стержня μ=1,0, а для стержня, жестко защемленного на обеих концах μ=0,5, т.е. гибкость такого стержня будет в два раза меньше первого…
Оставьте комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
25. Определение расчетных длин
От правильности задания расчётных длин элементов конструкций зависит надежность принятых конструктивных решений.
В большинстве случаев определение расчетных длин происходит согласно нормативных документов. Но нормативные документы рассматривают далеко не все возможные случаи.
В качестве примера рассматривается каркасное здание пролётом 10 метров с колоннами из двутавра 40К1 и ригелями из двутавра 40Б1 (рис. 1).
Рис. 1. Расчётная модель здания. ПК ЛИРА 10.
Дл я определения расчетных длин кол онн с определенной погрешностью можно использовать формулу 142 таблицы 31 СП 16.13330.2011, а для ригелей, которые в таких рамах, наряду с изгибом, испытывают также и сжатие, нормы не дают ответа по определению расчетной длины.
Поэтому, для определения расчетных длин элементов рамы в плоскости, воспользуемся подсистемой «устойчивость». Для этого возьмем плоскую раму и зададим на нее нагрузку для определения свободных длин (рис. 2).
Для анализа устойчивости схемы проектировщик должен составить характерное загружение, или характерную комбинацию загружений (РСН), по которой будет происходить определение расчетных длин элементов. Характерных загружений, или комбинаций загружений может быть несколько, для различных групп элементов. При этом следует руководствоваться п. 10.3.2 СП 16.13330.2011, согласно которому при определении расчетных длин следует брать сочетание, создающее наибольшие значения продольных сжимающих сил N в рассматриваемых элементах, и полученные расчетные длины использовать при проверке устойчивости для всех возможных комбинаций РСУ. Таким образом, для нашего объекта характерная комбинация загружений для определения расчетных длин включает (со своими коэффициентами сочетаний) все постоянные, длительные и снеговые загружения, но не включает ветер.
Рис. 2. Плоская рама для определения расчётных длин. ПК ЛИРА 10
В редакторе загружений выбираем Выполнять Анализ устойчивости (рис. 3).
Рис. 3. Настройка параметров для расчёта устойчивости
Далее переходим в результаты расчёта и выбираем результаты по устойчивости.
Необходимо смотреть на первую форму потери устойчивости, дающую максимальные расчётные длины. Расчёт устойчивости по характерной комбинации загружений подтвердил, что первой, наиболее опасной, формой потери устойчивости ожидаемо является кососимметричная форма (рис. 4).
Рис. 4. Первая форма потери устойчивости. ПК ЛИРА 10
Если в этом режиме нажать левой кнопкой мыши на элемент, то появиться таблица с характеристиками расчётной длины этого элемента (рис. 5).
При определении расчетных длин следует также иметь в виду, что для анализа устойчивости принято, чтобы продольные сжимающие силы N в пределах рассматриваемых участков были неизменными. В нашем случае, как для колонн, так и для ригелей имеется равномерно-распределённая составляющая нагрузки вдоль стержня, обеспечивающая плавное изменение усилия N, что не вполне корректно. Соответственно, меняется и расчётная длина элемента на различных участках. Чем больше сжимающая сила, тем меньше получается расчётная длина. Здесь проектировщик должен обращать внимание на то, чтобы эта равномерно-распределённая составляющая нагрузка вдоль стержня не играла бы решающую роль в работе стержня, а разброс расчётных длин в пределах конструктивного элемента был бы несущественным. Далее, следуя логике пункта 10.3.2 норм СП 16.13330.2011, расчётную длину элемента следует брать в том месте, где сила N максимальная, т. е. там, где расчётная длина минимальна. Однако, подозревая, что максимальный эффект от совместного действия силы N и момента Му в месте жёсткого соединения ригеля с колонной, мы бы рекомендовали брать величину расчётной длины как для колонны, так и для ригеля именно в этом месте.
Окончательный же выбор остаётся за автором расчёта.
Получаем для колонн расчётную длину 14.1 м, а для ригелей 13.3 м (рис. 6).
Если считать по формуле (142), расчётная длина колонны получилась бы 11.7 м. Однако, формула (142) не учитывает двускатную форму ригеля, а это при значительных уклонах может существенно повлиять на результат.
Рис. 5. Расчетная длина колонн. ПК ЛИРА 10
Рис. 6. Расчётная длина ригелей. ПК ЛИРА 10
Теперь, задав эти параметры в редакторе конструирования (рис. 7), можем производить расчёт конструирования и получать точные результаты по подбору и проверке МК.
Рис. 7. Задание параметров конструирования для колонн и ригелей. ПК ЛИРА 10
Более подробно методика определения расчетных длин и другие вопросы рассматриваются на наших курсах обучения. Будем рады видеть вас среди наших учеников.
Расчетная длина колонны или стены
При расчете колонн или стоек ферм постоянного по длине сечения требуется помимо всего прочего знать расчетную длину колонны или стойки. Знание расчетной длины также необходимо при расчете участка стены на прочность. При этом не имеет решающего значения, из какого материала изготовлена или проектируется колонна, стойка или стена. Ни дерево ни металл ни бетон ни пластик на значение расчетной длины почти не влияют. А вот способ закрепления рассчитываемой конструкции на опорах или на опоре влияет на значение расчетной длины весьма значительно.
Так, например, для колонны с высотой Н с жестким защемлением только на нижней опоре, другими словами, глубоко заделанной в фундамент или крепящейся к фундаменту анкерными болтами, расчетная длина будет в 4 раза больше, чем колонны с такой же высотой Н и жестким защемлением на нижней опоре, но дополнительно имеющей жесткое защемление сверху. Почему? Сейчас попробуем разобраться.
Теоретически все выглядит до смешного просто: чтобы определить расчетную длину, нужно умножить высоту (реальную длину) колонны, стойки или рассчитываемого участка стены на коэффициент μ, учитывающий способ закрепления на опорах:
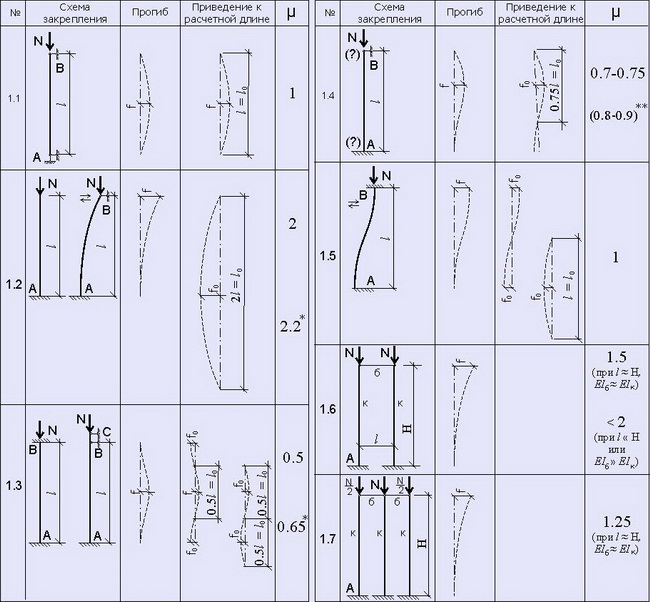
Если же Вы чувствуете в себе силы разобраться в нюансах закрепления, то милости просим. Проще всего это сделать по следующей таблице:
Значение коэффициента μ при нагрузке,
приложенной к верху (оголовку) колонны, стойки, стены.
При шарнирных опорах:
При жестком защемлении только на верхней опоре:
Как видим, теоретическая простота на деле распыляется на несколько вариантов. Даже при наличии всего двух вариантов вероятность выбора наугад правильного варианта составляет около 50%. При 7 представленных вариантах вероятность отгадывания правильного варианта падает значительно, поэтому мы не будем полагаться на волю случая, а более подробно рассмотрим указанные варианты.
Любая сжимаемая колонна или стойка или стена будет деформироваться, причем чем более неоднородным будет материал конструкции, чем сильнее его центральная ось будет отклонена от прямой линии и чем больше при этом соотношение длины конструкции к ширине или высоте поперечного сечения, тем больше вероятность того, что конструкция не сожмется как пружина, а выгнется как палка, на которую давишь. В таблице изменение положения центральной оси стержня показано пунктиром. Это приведет к появлению эксцентриситета приложения нагрузки, а значит и внутренние напряжения в изогнутой конструкции будут больше, чем в прямолинейной. Причем потеря устойчивости скорее всего произойдет относительно той оси, относительно которой соотношение длины к конструкции к одному из размеров поперечного сечения наибольшее. И хотя в данной статье рассматриваются некие стержни без привязки к каким-либо осям, но помнить об этом все-таки нужно.
Наиболее опасным с точки зрения потери устойчивости для стержней постоянного по всей длине сечения является поперечное сечение посредине длины стержня. В этом рассчитываемые на сжатие стержни похожи на симметрично или равномерно загруженные балки. В принципе если исхитриться и наклонить голову на 90 градусов и посмотреть на таблицу, то колонну от балки не отличишь. Как и для балки, для сжатой стойки или колонны очень важной характеристикой является величина прогиба, ведь чем больше прогиб, тем меньше несущая способность конструкции. Вот только как быстро определить этот прогиб? Ведь эпюры прогиба, характеризующие изменение положения центров тяжести поперечных сечений относительно центральной оси, при различных способах закрепления на опорах разные. И тогда какой-то умный человек придумал способ приведения различных расчетных схем к единому знаменателю, реализованный в таблице выше. Суть этого способа сводится к тому, чтобы одно из возможных закреплений балки взять за основу, а все остальные варианты закрепления стержней на опорах привести к основному использованием соответствующего коэффициента.
Наиболее заслуживающей доверия расчетной схемой является расчетная схема для колонны с жестким защемлением на нижней опоре (№1.2). Такая расчетная схема подходит для всех отдельно стоящих колонн, а также может применяться при колонн однопролетного и даже двухпролетного каркаса при соблюдении условий указанных для схемы №1.6.
Для колонн из древесины, металла и других материалов, на которые будут опираться балки перекрытия, на которые в свою очередь будет монтироваться перекрытие лучше использовать расчетные схемы №1.6 и №1.7.
Расчётная длина колонны
И в качестве продолжения озвученных вопросов: какой коэффициент расчётной длины применять к высоким колонная в продольной плоскости здания: двойку как для свободной рамы или всё же уменьшенный коэффициент? Можно ли ссылаться на результаты анализа устойчивости в Лире, которые ни при каких формах потери устойчивости не показывают расчётную длину колонны двойку (всегда видно, что колонна теряет устойчивость не как свободно стоящая).
Заранее спасибо за ответы.
Если хотите поточнее получить расчетную длину для правых колонн, нужно правую колонну рассчитать на устойчивость как отдельную колонну с пружинкой сверху. Жесткость пружинки можно получить, получив перемещения каркаса от горизонтальных единичных сил (лучше взять Qfic), приложенных к каркасу вверху рассматриваемых колонн (рассматриваемые колонны в этом случае или отбросить, или поставить сверху-снизу шарниры, чтобы не влияли на горизонтальную жесткость каркаса). Горизонтальное перемещения каркаса желательно получить в нелинейной постановке от всех расчетных нагрузок.
Спасибо большое, попробую, посмотрю, что получится
Спасибо большое, попробую, посмотрю, что получится
Я извиняюсь, но на 20м высоты будут 100% двухветвевые колонны. Там гибкость в плоскости рамы обыгрывается расстоянием между ветвями, незначительно увеличивая расход только решетки.
какие интересные узелки
omigo001, ваши связи ни хре фига не держат. Есть подозрения в большом количестве косяков в схеме.
Всем добрый день.
Напишу свои мысли.
Всем добрый день.
Напишу свои мысли.
какие интересные узелки
omigo001, ваши связи ни хре фига не держат. Есть подозрения в большом количестве косяков в схеме.
В чём проблема со связями?
Я извиняюсь, но на 20м высоты будут 100% двухветвевые колонны. Там гибкость в плоскости рамы обыгрывается расстоянием между ветвями, незначительно увеличивая расход только решетки.
Там в уровне диска должны быть распорки по колоннам высокой части, приходящие в систему вертикальных связей. Вообще система связей у вас. интересная
Расчетная длина колонны (стены)
При расчете колонн или стоек ферм постоянного по длине сечения требуется помимо всего прочего знать расчетную длину колонны или стойки. Знание расчетной длины также необходимо при расчете участка стены на прочность. При этом не имеет решающего значения, из какого материала изготовлена или проектируется колонна, стойка или стена. Ни дерево ни металл ни бетон ни пластик на значение расчетной длины почти не влияют. А вот способ закрепления рассчитываемой конструкции на опорах или на опоре влияет на значение расчетной длины весьма значительно.
Так, например, для колонны с высотой Н с жестким защемлением только на нижней опоре, другими словами, глубоко заделанной в фундамент или крепящейся к фундаменту анкерными болтами, расчетная длина будет в 4 раза больше, чем колонны с такой же высотой Н и жестким защемлением на нижней опоре, но дополнительно имеющей жесткое защемление сверху. Почему? Сейчас попробуем разобраться.
Теоретически все выглядит до смешного просто: чтобы определить расчетную длину, нужно умножить высоту (реальную длину) колонны, стойки или рассчитываемого участка стены на коэффициент μ, учитывающий способ закрепления на опорах:
lef = μl (233.1.1)
lo = μH (233.1.2)
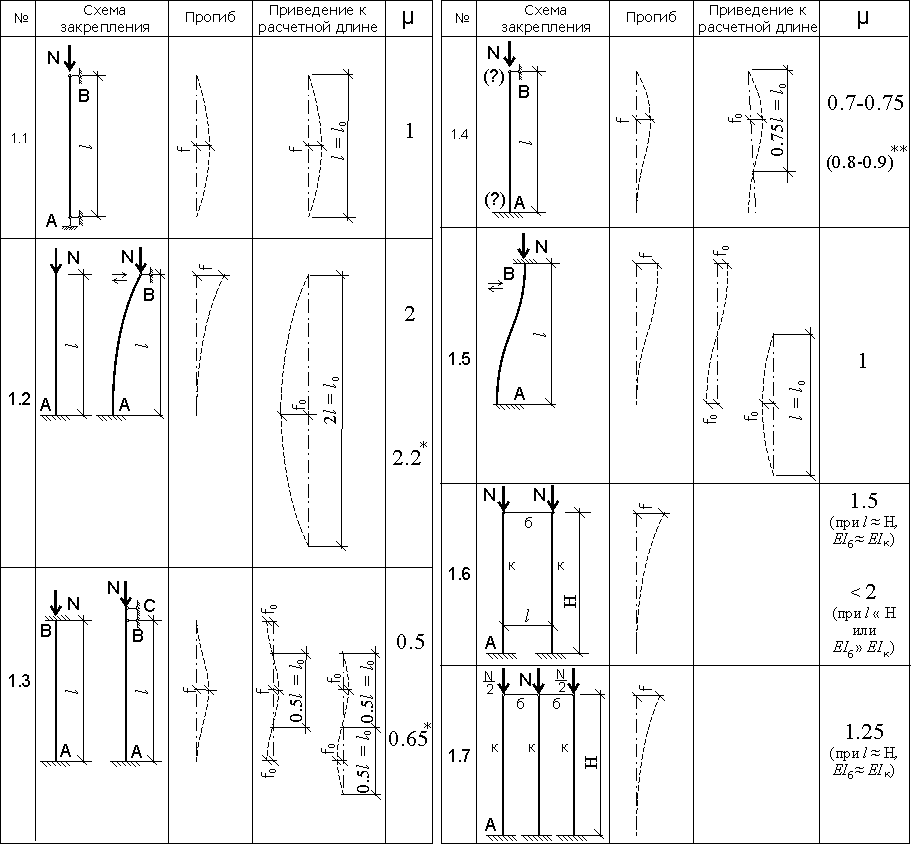
Если же Вы чувствуете в себе силы разобраться в нюансах закрепления, то милости просим. Проще всего это сделать по следующей таблице:
Таблица 233.1. Значение коэффициента μ при нагрузке, приложенной к верху (оголовку) колонны, стойки, стены.
При шарнирных опорах:
При жестком защемлении только на верхней опоре:
Как видим, теоретическая простота на деле распыляется на несколько вариантов. Даже при наличии всего двух вариантов вероятность выбора наугад правильного варианта составляет около 50%. При 7 представленных вариантах вероятность отгадывания правильного варианта падает значительно, поэтому мы не будем полагаться на волю случая, а более подробно рассмотрим указанные варианты.
Любая сжимаемая колонна или стойка или стена будет деформироваться, причем чем более неоднородным будет материал конструкции, чем сильнее его центральная ось будет отклонена от прямой линии и чем больше при этом соотношение длины конструкции к ширине или высоте поперечного сечения, тем больше вероятность того, что конструкция не сожмется как пружина, а выгнется как палка, на которую давишь, впрочем и очень длинную пружину тоже равномерно сжать не удастся и она тоже выгнется.
Наиболее опасным с точки зрения потери устойчивости для стержней на двух шарнирных опорах постоянного по всей длине сечения является поперечное сечение посредине длины стержня. В этом рассчитываемые на сжатие стержни похожи на симметрично или равномерно загруженные балки. В принципе если исхитриться и наклонить голову на 90 градусов и посмотреть на таблицу, то колонну от балки не отличишь. Как и для балки, для сжатой стойки или колонны очень важной характеристикой является величина прогиба, ведь чем больше прогиб, тем меньше несущая способность конструкции. Вот только как быстро определить этот прогиб? Ведь эпюры прогиба, характеризующие изменение положения центров тяжести поперечных сечений относительно центральной оси, при различных способах закрепления на опорах разные. И тогда какой-то умный человек, фамилии которого я не знаю (возможно это был математик Эйлер, впервые рассчитавший значение критической сжимающей силы, но утверждать не буду), придумал способ приведения различных расчетных схем к единому знаменателю, реализованный в таблице 233.1. Суть этого способа сводится к тому, чтобы одно из возможных закреплений балки взять за основу, а все остальные варианты закрепления стержней на опорах привести к основному использованием соответствующего коэффициента.
Вот в принципе и все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Доброго дня, Доктор!
Помогите решить вопросик. Имеется деревянный двухэтажный дом,брус 15х15, размер дома 8х9м внутри несущие стены делят его практически на четыре равные части.Есть идея выпилить одну стену на первом этаже и одну на втором. Как рассчитать максимально возможную величину проема, для того что бы эта великолепная конструкция не рухнула, крышу не повело и вообще не навредить строению. Есть какие либо формулы для расчета «от обратного».
Буду весьма признательна за пояснения
Формул всяких много есть. Вот только в вашем случае лучше пригласить инженера, чтобы он по месту определил конструктивную схему вашего здания и предложил оптимальный вариант.
Добрый день, док!
Почему у Вас в расчетах для деревянных конструкций часто расчетная длина равна фактической, т.е. коэффициент равен 1? Ведь там больше подойдет схема 1.6/1.7? Или это поправка на диафрагму жесткости такая? Какую схему целесообразно применить для расчёта стойки в каркасной стене прямоугольного/квадратного дома?
Как определить расчетную длину торцевой самонесущей стены 4-х этажного дома, если плиты перекрытий на нее совсем не заходят. Расчетная схема 1.1 или 1.2?
Такая стена будет иметь перевязку с наружными, возможно и с внутренними стенами, поэтому рассматривать ее по всей высоте, как отдельно стоящую колонну будет не совсем корректно. Тем не менее для упрощенных расчетов можете воспользоваться расчетной схемой 1.1.
А для расчета опор(ног) козлового крана какая схема ближе? Опоры при виде сбоку имеют угол Крепление опор вверху и внизу стяжками на болтах.
Если крепления опор (болты) рассчитаны на возникающие усилия и обеспечивают неподвижность, то можно воспользоваться схемой 1.3. Но для надежности лучше воспользоваться схемой 1.1. А угол наклона опор козлового крана влияет только на определение вертикальной составляющей нагрузки. Примерно так.
Добрый день! Подскажите, может ли расчетная длина среднего участка двухступенчатой колонны быть в три раза больше чем общая геометрическая высота колонны? (считаю по СП «Стальные конструкции», приложение И)
Вы представили слишком мало данных. Но теоретически, при жестком защемлении внизу и свободном верхнем конце это возможно. Тут главное не забывать, что любой рассматриваемый участок колонны по-прежнему остается частью общей колонны, просто рассматривается отдельно, в зависимости от имеющихся геометрических характеристик.
В то же время, если в районе ступеней имеются дополнительные горизонтальные связи, то это позволяет рассматривать каждый участок колонны отдельно и тогда расчетная длина каждого участка будет меньше или равна реальной высоте участка. Впрочем тут нужно смотреть на ситуацию в целом. Как я уже говорил данных для анализа вы представили не достаточно.
Подскажите расчетную длину колонны.Заранее спасибо, Dr.LOM.
Какой именно колонны?
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).