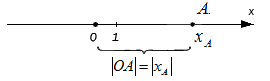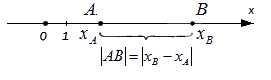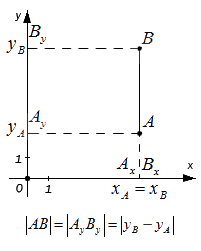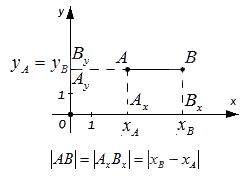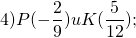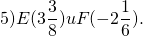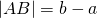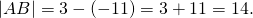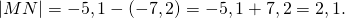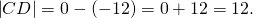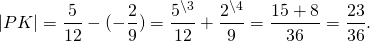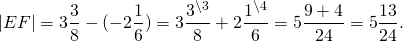Что такое расстояние между двумя точками 6 класс

Расстояние от точки до точки: формулы, примеры, решения

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

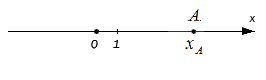
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A

Расстояние между точками на плоскости

— если точки А и В совпадают, то расстояние между ними равно нулю;

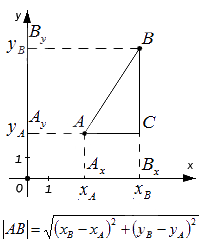
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

Расстояние между точками в пространстве

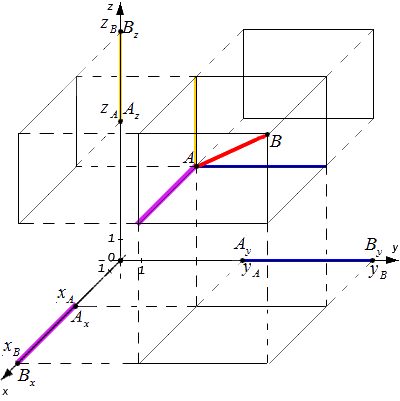
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2

Используя полученные ранее выводы, запишем следующее:

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

Полученная формула действительна также для случаев, когда:

— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Решение

Решение

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Решение

Источник

Конспект урока математики 6 класс по теме «Расстояние между двумя точками на координатной прямой»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Конспект урока по математике 6 класс

Тема: «Расстояние между точками координатной прямой»

Цель урока : Организация деятельности обучающихся для :

овладения навыком находить расстояние между точками координатной прямой, вычисляя модуль разности, координаты середины отрезка ;

развития у учащихся умения самостоятельно добывать знания, самоконтроля и самооценки.

Представление о результатах:

личностные – уважительное и доброжелательное отношение к другому человеку, его мнению; готовность и способность вести диалог с другими людьми и достигать в нем взаимопонимания ;

метапредметные – выдвигать версии решения проблемы, формулировать гипотезы, предвосхищать конечный результат;

предметные – нахождение расстояния между точками координатной прямой, координаты середины отрезка .

продолжить развитие логического мышления учащихся;

организовать деятельность обучающихся таким образом, чтобы они смогли сделать самопроверку, взаимопроверку, самоконтроль.

1. Организационный момент.

2. Проверка домашнего задания.

3. Устный счет (на слайде).

— Вы узнаете тему урока, если найдете значения выражений и запишите соответствующие буквы в таблицу ответов.

— Итак, тема нашего урока «Расстояние между точками координатной прямой».

4. Теоретический опрос.

— Какие числа называются целыми?

(Целые числа – это натуральные числа, им противоположные и ноль).

— Какие числа называют противоположными?

(Противоположные числа – это числа, имеющие одинаковые модули, но отличающиеся знаком).

— Как сложить два числа с разными знаками?

(Для того, чтобы сложить два числа с разными знаками необходимо из модуля большего числа вычесть модуль меньшего числа и поставить знак больше модуля).

— Как сложить два числа с одинаковыми знаками?

(Для того, чтобы сложить два числа с одинаковыми знаками, мы складываем их модули и ставим общий знак).

— Что такое модуль числа?

(Модулем числа называют расстояние от определенной точки до начала отсчета).

— Чему равно расстояние между точками координатной прямой?

(Расстояние между точками координатной прямой равно модулю разности координат этих точек).

5.Закрепление изученного материала.

Решение номеров из учебника у доски, дети, работающие в более высоком темпе, получают дополнительные задачи на карточках.

— Решаем номера из учебника: № 296 (в, г), 297 (в, г), 300 (в)

Отмечаем данные по условию точки на координатном луче:

— А теперь решим с вами такую задачку:

Наш город, Нерчинск находится между городами Чита и Сретенск. Расстояние от Нерчинска до Читы 272 км, от Сретенска до Читы 359 км. Найдите расстояние от Сретенска до Нерчинска.

Ответ: расстояние от Сретенска до Нерчинска составляет 87 км.

7. Проверочная работа.

— Сейчас вам предлагается выполнить проверочную работу, задания вы можете увидеть на слайде. Время работы 5 минут. За задачу № 3* ставится отдельная оценка.

1. Найдите расстояние

2. На координатной прямой отмечены точки

3*. Расстояние от города Нерчинска до поселка Приисковый 10 км, а расстояние от поселка Приисковый до села Калинино – на 20% меньше. Найдите расстояние от города Нерчинска до села Калинино.

1. Найдите расстояние

2. На координатной прямой отмечены точки

3*. Расстояние от села Березово до поселка Заречный 15 км, а расстояние от поселка Заречный до города Нерчинска – на 60% меньше. Найдите расстояние от села Березово до города Нерчинска.

— Поменяйтесь тетрадью с соседом, возьмите в руки простые карандаши и проверьте друг друга (ответы на слайде).

8. Постановка домашнего задания

Учитель записывает домашнее задание на доске.

— Откройте дневники, запишите домашнее задание:

, № 1*, № 2* (на карточках для более сильных учеников).

— Номера со звездочкой для любознательных ребят.

— А теперь положите дневники в открытом виде на край стола для проверки записи домашнего задания.

— «Что на уроке вам было особенно интересно?»

— «Что вызвало трудности?»

— «Что еще по данной теме вы хотели бы узнать?»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-789266

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В МГПУ сформулировали новые принципы повышения квалификации

Время чтения: 4 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Школьники из Москвы выступят на Международной олимпиаде мегаполисов

Время чтения: 3 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Педагогам Северной Осетии в 2022 году будут выплачивать надбавки за стаж

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

«Расстояние между двумя точками. Масштаб» (6 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема: Расстояние между двумя точками. Масштаб.

Цель урока: повторить понятие расстояния между двумя точками; показать применение масштаба в повседневной жизни; развивать в детях умение работать в коллективе и воспитывать в детях уверенность в себе; развивать интерес к математике и показать связь математики с другими науками, в частности с географией.

Тип урока: Урок обобщения и систематизации знаний

Математика 5 класс И.И.Зубарева, А.Г. Мордкович

Индивидуальные карточки для групповой работы,

мультимедийная установка, интерактивная доска.

показать применение масштаба в повседневной жизни;

развивать в детях умение работать в коллективе и воспитывать в детях уверенность в себе;

развивать интерес к математике и показать связь математики с другими науками, в частности с географией.

I. Организационный момент.

Разбить класс на группы.

II. Актуализация знаний.

Презентация. (Приложение1. Приложение 2).

1. Фронтальная работа с классом.

1) Масштаб карты квартала 1: 1000. Найди данные расстояния в реальности:

• от школы до Петиного дома 3 см;

• от Петиного дома до бассейна 7 см;

• от Петиного дома до Мишиного дома 8 мм;

• от Петиного дома до ближайшего магазина 5 мм.

2) Какое расстояние будет на карте с тем же масштабом, если в реальности:

• от школы до районо 3 км;

• от школы до театра ТЮЗ 10 км;

• от школы до магазина 300 м.

3) Можно назвать расстоянием путь, который проходит поезд от Саратова до Самары?

Если преодолеть путь от Саратова до Ростова на автобусе, будет ли этот путь расстоянием между этими городами?

Из Саратова до Москвы можно добраться на самолете, будет ли этот путь являться расстоянием между этими городами?

III. Работа с картой.

Для чего нам нужен масштаб? На этот вопрос поможет отве­тить карта России.

Каждой группе раздается карточка. На карточке название города, в который предлагается совершить путешествие, указана скорость самолета, с которой это путешествие будет совершаться.

1) Москва. V = 650 км/ч.

2) Санкт-Петербург. V = 800 км/ч.

3) Нижний Новгород. V = 700 км/ч.

4) Томск. V = 900 км/ч.

5) Самара. V = 750 км/ч.

Алгоритм работы с картой:

• Повторить понятие расстояния.

• Найти на карте России город, заданный на карточке, и город Саратов.

• Перевести расстояние в реальные размеры с помощью мас­штаба.

• Найти время пути, зная расстояние и скорость.

Задание: найти время, за которое будет совершен перелет из одного города в другой.

Для презентации своей работы группа выбирает одного человека.

IV. Практическое задание «Ремонт в квартире».

Цель: показать использование масштаба в повседневной жизни.

Задание: подсчитать, в какую сумму обойдется ремонт полов в заданном помещении

из данного материала. Каждой группе раздаётся план квартиры:

1. Линолеум – 400 р. За 1 кв.м.

3. Кавролин – 300 р. 1 кв.м.

4. Паркет – 600 р. За 1 кв.м.

Группам предлагается одна из карточек.

1. Сделать ремонт в столовой.

2. Материал покрытия выбрать самостоятельно.

3. Сделать расчет, используя алгоритм.

Алгоритм работы составляется учащимися:

• Измерение параметров нужного помещения.

• Перевод с помощью масштаба величин в реальные размеры.

• Выбор покрытия полов.

• Подсчет расходов на материал для ремонта.

V. Подведение итогов.

Наш президент собирается посетить несколько городов с визи­тами и провести в них различные совещания. Совещания у прези­дента длятся 3 часа. Ему нужно посетить следующие города: Сара­тов, Омск, Казань, Владивосток. Вылетает он из Москвы на само­лете, скорость которого 900 км/ч, и ему нужно как можно быстрее вернуться в столицу. Составить последовательность посещений таким образом, чтобы поездка заняла как можно меньше времени.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-095434

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Более 50 российских школ перешли на дистанционку из-за коронавируса

Время чтения: 1 минута

Псковских школьников отправили на дистанционку до 10 декабря

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Расстояние между точками на координатной прямой

Расстояние между двумя точками на координатной прямой равно модулю разности их координат.

Формула расстояния между точками на координатной прямой:

где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.

Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.

Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:

Ответ. Расстояние между точками L и M равно 8.

Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).

Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:

10 : 2 = 5, значит |AC| = |CB| = 5.

Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:

Ответ. Координата середины отрезка C(0).

Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).

Ответ. Координата точки C — 16.

Источник

Расстояние между точками на координатной прямой

Расстоянием между двумя точками A и B называется длина отрезка, соединяющего эти точки.

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату левого конца.

Найти расстояние в единичных отрезках между точками:

Чтобы найти расстояние между точками на координатной прямой, определим, какая из точек находится правее, и из координаты правого конца отрезка вычтем координату его левого конца.

Из двух точек на координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.

Для точек A(a) и B(b) это означает, что если b>a, то точка B на координатной прямой лежит правее точки A и расстояние между точками A и B равно

3) Так как 0>-12, точка C (0) на координатной прямой лежит правее точки D(-12). Расстояние между точками C и D:

— \frac<2><9>,\]» title=»Rendered by QuickLaTeX.com»/>

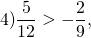
поэтому точка K на координатной прямой расположена правее, чем точка P.

— 2\frac<1><6>,\]» title=»Rendered by QuickLaTeX.com»/>

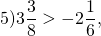
значит, точка E на координатной прямой находится справа от точки F. Поэтому длина отрезка EF, а значит, и расстояние между точками E и F

2 Comments

Для чего находить наибольшее число, если |a-b|=|b-a|?

Дмитрий, всё зависит от учебника. Если данную тему изучают после того, как ввели понятие модуля, то расстояния между точками на координатной прямой можно искать как модуль разности координат этих точек. В противном случае действуем, как описано выше.

Источник