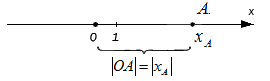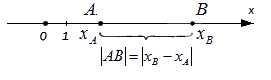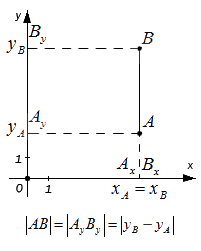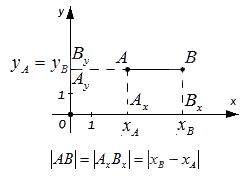Что такое расстояние между точкой и прямой

Расстояние от точки до прямой онлайн

С помощю этого онлайн калькулятора можно найти расстояние от точки до прямой. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до прямой, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Расстояние от точки до прямой − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Расстояние от точки до прямой на плоскости

Пусть в двухмерном пространстве задана точка M₀(x₀, y₀) и прямая L:

где q=(m,p) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (1)(Рис.1).

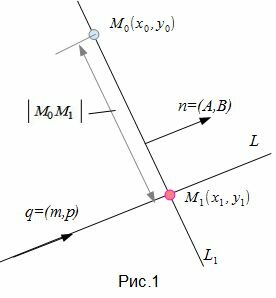Алгоритм нахождения расстояния от точки M₀ до прямой L содержит следующие шаги:

Уравнение прямой, проходящей через точку M₀(x₀, y₀) имеет следующий вид:

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M₀ на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

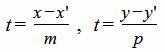Подставим значения x и y в (4):

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M₀ на прямую L:

Далее находим расстояние между точками M₀ и M₁ используя формулу:

Пример 1. Найти расстояние от точки M₀(−6, 2) до прямой

Направляющий вектор прямой (8) имеет вид:

Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x₀, y₀, x’, y’ в (6):

Подставляя значение t в (5), получим:

Вычислим расстояние между точками M₀(-6, 2) и M₁

Расстояние от точки M₀(-6, 2) до прямой (8) :

2. Расстояние от точки до прямой в пространстве

где q=(m, p, l) направляющий вектор прямой L.

Найдем расстояние от точки M₀ до прямой (9)(Рис.2).

Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:

где n=(A,B,C) нормальный вектор плоскости α.

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M₀ на прямую L, выведем параметрическое уравнение прямой (9):

Подставим значения x и y в (11):

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M₀ на прямую L:

Далее вычисляем расстояние между точками M₀ и M₁ используя формулу

,

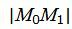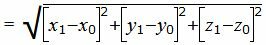(14)

которое является расстоянием между точкой M₀ и прямой (9).

Пример 2. Найти расстояние от точки M₀(1, 2, 1) до прямой

Направляющий вектор прямой (15) имеет вид:

Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x₀, y₀, z₀ x’, y’, z’ в (13):

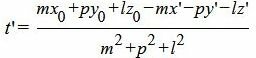Подставляя значение t=t’ в (12), получим координаты точки M₁:

Далее, используя формулу (14) вычисляем расстояние от точки M₀ до прямой (15):

.

.

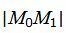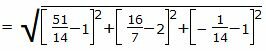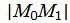Расстояние от точки M₀(1, 2, 1) до прямой (15) :

Источник

Определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П₄. В новой системе (П₁, П₄) точки C»₁, D»₁, M»₁ находятся на том же удалении от оси X₁, что и C», D», M» от оси X.

Выполняя вторую часть алгоритма, из M»₁ опускаем перпендикуляр M»₁N»₁ на прямую b»₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»₁N»₁. Для этого строим прямоугольный треугольник M»₁N»₁N₀, у которого катет N»₁N₀ равен разности (Y_M1 – Y_N1) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M»₁N₀ треугольника M»₁N»₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

Источник

Формула нахождения расстояния от точки до прямой

Что такое расстояние от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую.

При этом перпендикуляр – это наименьшее из расстояний от этой точки до точек прямой.

Расстояние от точки до прямой на плоскости, методы нахождения

Найти расстояние от точки до прямой можно двумя способами. С помощью теоремы Пифагора или прямоугольной системы координат. Рассмотрим первый метод.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема Пифагора гласит, что прямоугольная система координат OXY имеет точку М₁ (x₁, y₁). Из нее к плоскости проведена прямая а. Уравнение плоскости имеет вид:

Это уравнение равно по модулю значению, которое получается в левой части уравнения прямой при x = x₁, а y = y₁. Это значит, что:

Доказательство

Прямой а соответствует уравнение плоскости, которое имеет вид:

Что и следовало доказать.

Согласно теореме Пифагора, чтобы найти расстояние от точки до прямой, нужно совершить следующие шаги:

Рассмотрим второй метод. Если у точки Н₁ есть координаты (х₂, у₂), тогда расстояние от точки до прямой можно найти по формуле:

Найдем координаты точки Н1.

Прямая линия в ОХУ равна уравнению прямой на плоскости. Необходимо составить уравнение прямой b, проходящей через точку М₁ перпендикулярно прямой а. Н₁ – это точка пересечения прямых a и b. Для начала нужно найти общее уравнение прямой а, которое имеет вид А₁х + В₁у + С₁ = 0. Либо можно воспользоваться уравнением с угловым коэффициентом у = k₁x + b₁.

Далее нужно вывести уравнение прямой b, которое имеет вид А₂х + В₂у + С₂ = 0. Либо можно использовать уравнение по аналогии с прямой а: у = k₂x + b₂. Чтобы определить координаты точки Р1, нужно решить систему линейных уравнений:

Конечное расстояние получают с помощью формулы:

Формулы для нахождения расстояния

Длину перпендикуляра также можно найти с помощью следующей формулы:

Решение уравнений

Пример 1

Решение

Пример 2

Решение

Пример 3

Решение

Примеры задач для нахождения расстояния от точки до прямой

Задача 1

Дана треугольная пирамида АВСD. Ее грани ABС и ABD представляют собой равные равнобедренные треугольники с прямыми углами при вершине A.

Найти расстояние от точки A до грани ACD, если высота пирамиды равна h и равна CD.

Решение

Так как △BCD равнобедренный, то BC ⊥ CD, K – середина CD. Так же AK ⊥ CD. Получается, перпендикуляр BH на плоскость ACD упадет на прямую AK (удовлетворяет теореме о трех перпендикулярах: HK – проекция, BK – наклонная, обе перпендикулярны CD).

Задача 2

Дана правильная четырехугольная пирамида ABCDE с вершиной A. Через точку пересечения диагоналей основания провели плоскость α перпендикулярно ребру AB.

Решение

По теореме о трех перпендикулярах AB ⊥ CE как наклонная (AO ⊥ (BCD), OB ⊥ CE – проекция). Получаем две пересекающиеся прямые OK и СЕ из плоскости α. Значит, сечением является треугольник СKЕ.

Проведем MN ∥ СЕ. Тогда MN ∥ α. Так как расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то:

Т.к. по условию SA⊥α, то проведем QH∥SA⇒QH⊥α. По построению MN – средняя линия △BAD, следовательно:

ВQ = QO ⇒ QH – средняя линия △ KВO ⇒ QH = \frac12 ВK.

Задача 3

Дано: в цилиндре параллельно диаметру ВС = 10 в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках Р и Z, причем PZ = 6. Через отрезок PZ проведена плоскость α под углом 15 градусов к плоскости осевого сечения ВСDE.

Найти расстояние от центра нижнего основания до плоскости α.

Решение

Обозначим за OQ – ось цилиндра. Тогда OQ ⊥ BC ⇒ OQ ⊥ p (OQ ∩ p = L).

Проведем OR ⊥ PZ ⇒ по теореме о трех перпендикулярах RL ⊥ PZ ⇒ RL ⊥ p ⇒ ∠ RLO – угол между плоскостями BCDE и α.

Так как и OR⊥PZ и LR⊥PZ, то перпендикуляр из точки O на плоскость α упадет на прямую LR.

Рассмотрим △ OPR: OP = 5, PR = 3, ∠ ORP = 90° ⇒ OR = 4.

Источник

Расстояние от точки до точки: формулы, примеры, решения

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

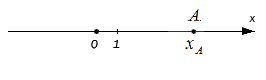
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A

Расстояние между точками на плоскости

— если точки А и В совпадают, то расстояние между ними равно нулю;

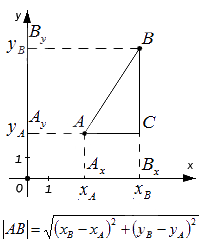
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:

Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:

Расстояние между точками в пространстве

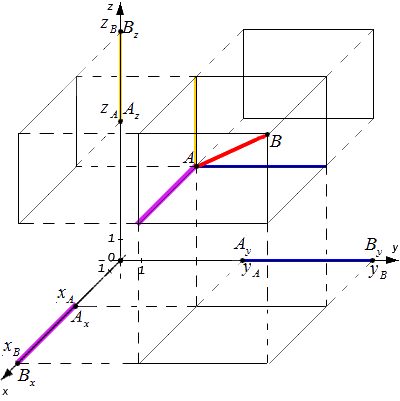
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2

Используя полученные ранее выводы, запишем следующее:

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

Полученная формула действительна также для случаев, когда:

— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Решение

Решение

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Решение

Источник

Расстояние от точки до прямой

Вы будете перенаправлены на Автор24

Основные определения и теоремы

Расстояние — это мера, характеризующая удалённость нескольких объектов друг относительно друга. Термин “расстояние” применим как в пространстве, так и на плоскости.

Рассмотрим небольшую иллюстрацию.

Мы видим на рисунке 2 точки. Необходимо найти расстояние между ними.

Для выполнения данной задачи необходимо использовать любой измерительный инструмент, например, линейку.

Необходимо приложить его начало к одной из точек, а конец к другой, и списать полученное с линейки число.

Также для измерения можно использовать, например, циркуль. С помощью него можно даже измерять толщину складок жира, прикладывая циркуль после снятия замера к линейке.

Перейдём к рассмотрению частного случая: поиску расстояния между точкой и прямой.

Расстояние между точкой и прямой

Рассматривая прямую и точку, не возлежащую на ней, следует помнить, что они всегда образуют плоскость по одной из основных аксиом объёмной геометрии, поэтому рассматривать эту задачу можно как одну из планиметрических.

Рисунок 3. Точка и не проходящая через неё прямая — служат характеристиками плоскости

Теорему, об образовании одной-единственной плоскости точкой и прямой можно вывести из аксиомы, в которой говорится, что три точки описывают плоскость.

Готовые работы на аналогичную тему

Дело в том, что на любой прямой всегда можно отметить 2 произвольные несовпадающие точки, а некая третья точка у нас уже дана. Вот и всё доказательство теоремы.

Расстояние между точкой и прямой — это перпендикуляр, который опускают с этой прямой в рассматриваемую точку.

Рассмотрим, что же такое расстояние от точки до прямой на примере задачи ниже.

Расстояние от точки до прямой на плоскости

Рисунок 4. Найти расстояние от точки до прямой

Одной из наиболее частых задач по данной теме на плоскости и в пространстве является определение расстояния от прямой до точки по координатам точки и уравнению прямой.

На практике обычно не очень удобно заниматься таким построением в масштабе 1:1, поэтому обычно поиск кратчайшей длины между точкой и прямой осуществляется аналитически.

Рассмотрим решение такой задачи на плоскости.

Определить расстояние между точкой и прямой.

Нормальный вектор для этой прямой является направляющим для перпендикуляра.

Следовательно, мы можем записать его уравнение:

И затем подставляем его в первое:

Подставляем полученный икс во второе уравнение:

Расстояние от точки до прямой в пространстве

При определении расстояния от точки до прямой в пространстве можно воспользоваться следующей формулой:

Эта формула также выведена из построений, аналогичных построением при решении подобной задачи на плоскости, но выглядит она более тяжеловесно.

Однако, этого не стоит пугаться, так как довольно удобно пользоваться.

Но, возможно, что новичкам перед её использованием придётся ознакомиться с тем, как высчитывать определитель матрицы.

Рассмотрим задачу с использованием этой формулы.

Подставим все эти числа в формулу для нахождения расстояния:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 12 07 2021

Источник