Что такое расстояние в геометрии 7 класс

Расстояние от точки до прямой

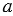
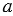
Пусть нам даны прямая и точка А, не лежащая на данной прямой. Опустим из точки А к прямой перпендикуляр АН и соединим точку А с произвольной точкой М, лежащей на прямой А и отличной от Н.

Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.

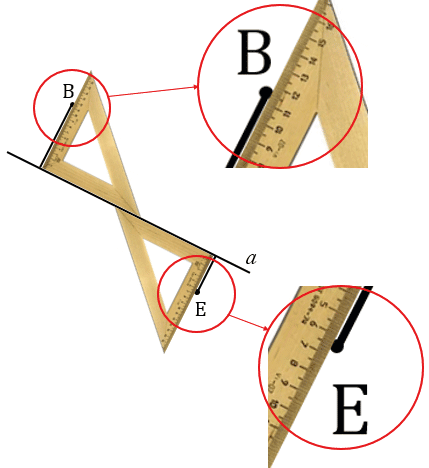
Для того, чтобы найти расстояние от точки до прямой, нужно с помощью чертежного угольника провести перпендикуляр из данной точки к данной прямой, а затем измерить длину этого перпендикуляра.

Расстояние от точки Е до прямой 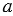равно 6,5 см, расстояние от точки В до прямой равно 11,5 см.

Поделись с друзьями в социальных сетях:

Источник

Геометрия. 7 класс

Расстояние от точки до прямой. Расстояние между параллельными прямыми

Перпендикуляр

Расстояние

Треугольник

Равнобедренный треугольник

Расстояние между параллельными прямыми

Необходимо запомнить

Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямой, не являющийся перпендикуляром к прямой.

Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.

Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.

Параллельность прямых

Докажем утверждение: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.

Доказать: точки A, B, C – принадлежат одной прямой.

Источник

61. Стереометрия Читать 0 мин.

61.333. Расстояния

Расстояния

Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.

Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.

В стереометрии найти расстояние можно между следующими комбинациями фигур:

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ

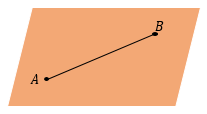
Расстояние между точками– это длина отрезка, соединяющего эти точки.

В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.

То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.

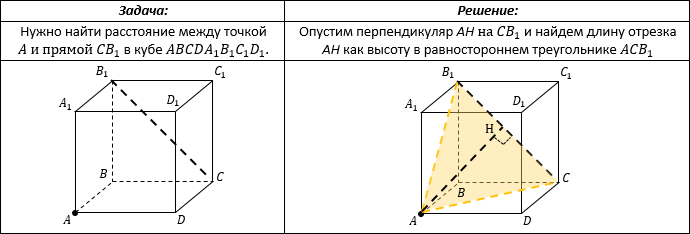
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ

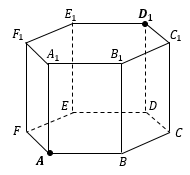
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.

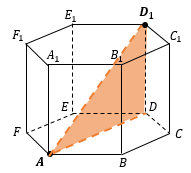
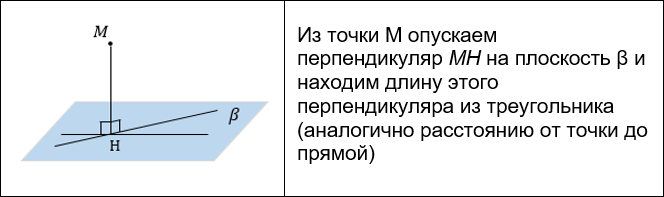
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ

Существует несколько способов нахождения расстояния от точки до плоскости:

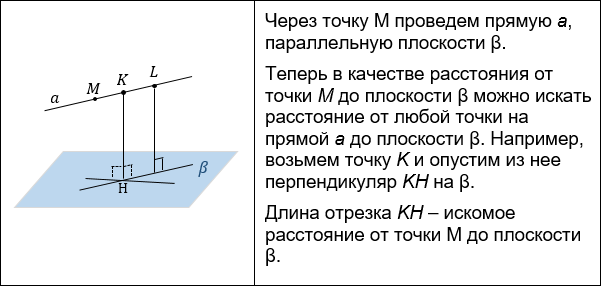
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Существует несколько способов нахождения расстояния между скрещивающимися прямыми:

1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.

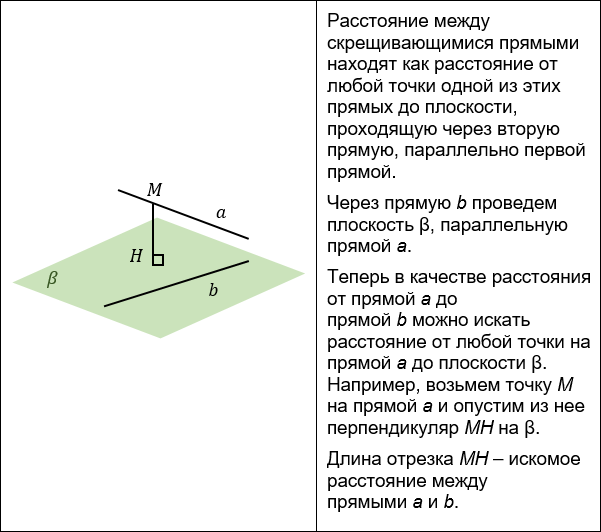
3. Построение параллельной плоскости.

Источник

Расстояние от точки до прямой. Расстояние между параллельными прямыми

Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой. Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой. Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой. На рисунке 137 расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.

Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.

Рассмотрим параллельные прямые а и B. Отметим на прямой а точку А и проведём из этой точки перпендикуляр АВ к прямой B (рис. 138). Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.

Проведём из точки X перпендикуляр ХУ к прямой B. Так как ХY ⊥ b, то ХY ⊥ a. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY — общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых а и B секущей AY). Следовательно, ХY = АВ.

Итак, любая точка X прямой а находится на расстоянии АВ от прямой B. Очевидно, все точки прямой b находятся на таком же расстоянии от прямой а. Теорема доказана.

Источник

Геометрия. 7 класс

Конспект урока

Расстояние от точки до прямой. Расстояние между параллельными прямыми

Перечень рассматриваемых вопросов:

Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямойине являющийся перпендикуляром к прямой.

Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.

Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Теоретический материал для самостоятельного изучения.

Расстояние между двумя точками – длина отрезка, соединяющего эти точки. Введём также следующие понятия:

1) расстояние от точки до прямой;

2) расстояние между параллельными прямыми.

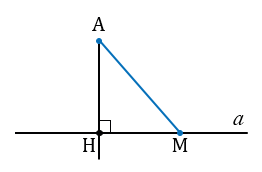
Пусть отрезок АН – перпендикуляр, проведённый из точки А к прямой а, М – любая точка прямой а, отличная от Н. Отрезок АМ называется наклонной, проведённой из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы АМ. Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.

Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.

Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.

На рисунке расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.

Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.

Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Доказательство. Рассмотрим параллельные прямые а и b. Отметим на прямой a точку A и проведём из этой точки перпендикуляр AB к прямой b. Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.

Проведём из точки Х перпендикуляр XY к прямой b. Так как XY‎ перпендикулярно b, то XY‎ перпендикулярно а. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY). Следовательно, XY = AB.

Итак, любая точка X прямой a находится на расстоянии AB от прямой b. Очевидно, что все точки прямой b находятся на таком же расстоянии от прямой a. Теорема доказана.

Из доказанной теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Отметим, что расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.

Замечание. Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.

Доказательство: по аксиоме параллельных прямых, через точку A проведем прямую b, b║a, тогда все точки b║a равноудаленыот точек прямой a. Докажем, что B, C∈ b.

Пусть B∉ b, C∉ b, значит, расстояние от точки B до a и C будет больше или меньше, чем расстояние h. Но это противоречит AA₁ = BB₁ = CC₁.

Следовательно, наше предположение неверно и A, B и С ∈ b || a, что и требовалось доказать.

Разбор заданий тренировочного модуля.

В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 12 см. Найти расстояние от точки A до прямой BC.

Объяснение: равносторонним треугольником называется треугольник с тремя равными сторонами (значит, и с тремя равными углами, то есть – по 60°). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD⊥BC

Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую AC, то DH – данное расстояние. Рассмотрим треугольник AHD. В нём угол H = 90°, так как DH – перпендикуляр к AC (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла DAH = 30°, поэтому AD = 2 ∙ 12= 24см (по свойству).

Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD⊥ BC, значит, AD = 24 см.

Источник