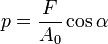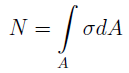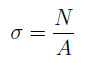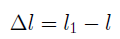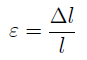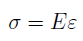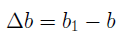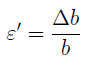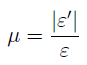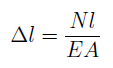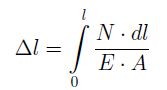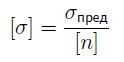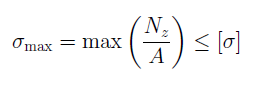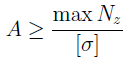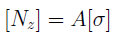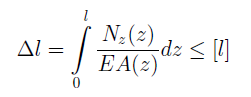Что такое растяжение сопромат

Тема 2.2. Растяжение и сжатие

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.

Рис. 1. Растяжение стержня

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2, б).

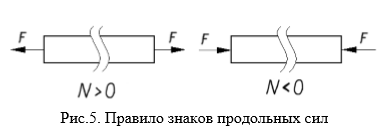
Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z направлена от сечения (рис. 2, б), а при сжатии – к сечению.

Рис. 2. Нормальная сила N

Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).

Рис. 3. Знак продольной силы N

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N_z). Он дает наглядное представление о законе изменения продольной силы.

Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

§2. Напряжение в поперечных сечениях стержня

Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия

§3. Расчеты на прочность и жесткость при растяжении-сжатии

Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],

Данное выражение определяет условие прочности при растяжении или сжатии.

С помощью этой формулы решается три вида зада (выполняется три вида расчета):

1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].

В случаях, когда рабочее напряжения значительно ниже допускаемых σ

Источник

Что такое растяжение и сжатие?

Растяжение и сжатие является первым разделом с которым знакомятся студенты в рамках сопромата. Растяжение (сжатие) – это такой способ воздействия на стержень при котором в его поперечных сечениях возникает только одно внутреннее усилие – продольная сила.

Какие существуют виды растяжения и сжатия?

Указанное выше определение относится только к центральному растяжению или сжатию, то есть все внешние силы, в этом случаем, прикладываются к центру тяжести поперечных сечений, то есть они направленны вдоль оси стержней. В сопромате есть более сложный вид растяжения при котором силы прикладываеются внеценртенно, а в поперечных сечениях в ответ появляется сразу несколько внутренних силовых факторов. Для решения задач на данную тематику потребуются знания сразу нескольких разделов сопромата, поэтому будем продвигаться постепенно, начиная с более простых тем, данная статья будет посвященна только центральному растяжению и сжатию.

Метод сечений и растяжение (сжатие)

Как говорилось выше, в центрально растянутых или сжатых элементах конструкций возникают только продольные усилия. Как узнать численное значение этих сил? Для их определения сопроматчики пользуются методом сечений. В чем собственно этот метод заключается? Если тело нагружено внешними силами находится в равновесии, то и отдельные части этого тела будут находится в равновесии. Данный метод позволяет устанавливать связь между внутренними и внешними силами. Рассмотрим этот метод в действии на примере бруса, который растягивается какой-то внешней силой.

Например, если мы хотим узнать продольное усилие в поперечном сечении, находящемся справа от свободно торца бруса на расстоянии x, мысленно рассекаем брус в намеченном месте, компенсируем действие одной части бруса на другую прикладывая силы N, то есть уравновешиваем одну часть и другую, тем самым сила N и будет той искомой внутренней продольной силой, не трудно догадаться что эта сила будет численно равна внешней силе F.

Отличием здесь служит только направление этих сил. Так же очевидно, что в каком бы месте бруса мы не делали сечение и находили продольную силу, она бы всегда была равна внешней. Отсюда, формулируем полезное правило, которое в дальнейшем обязательно пригодится: если в пределах участка нагруженного стержня действует только постоянная внешняя сила, то в поперечных сечениях стержня на данном участке будут возникать одинаковые внутренние усилия, которые численно будут равны внешней силе.

На практике в стержнях по всей длине могут возникать различные по величение продольные силы. Для того чтобы отслеживать их величину по всей длине, сопроматчики придумали строить так называемые эпюры продольных сил.

Эпюра в сопромате – это график показывающий распределение какой-либо величины по длине нагруженного элемента.

Источник

Растяжение (в сопротивлении материалов)

Растяжение-сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс).

Называется также одноосным или линейным напряжённым состоянием. Является одним из основных видов напряжённого состояния параллелепипеда. Может быть также двух- и трёх-осным. [1] Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).

Растяжение вызывает удлиннение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).

В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает т. н. внецентренное растяжение (сжатие). В этом случае за счёт эксцентриситета приложения нагрузки в стержне кроме растягивающих (сжимающих) напряжений возникают ещё и изгибные напряжения.

Напряжение вдоль оси прямо пропорционально растягивающей или сжимающей силе и обратно пропорционально площади поперечного сечения. При упругой деформации между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их на коэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами.

Напряжения в растянутом или сжатом стержне

Разложим напряжения p на нормальную σ_α и касательную составляющие. Продолжение следует.

Примечания

Полезное

Смотреть что такое «Растяжение (в сопротивлении материалов)» в других словарях:

Растяжение (в сопротивлении материалов) — Растяжение в сопротивлении материалов, см. Растяжение сжатие … Большая советская энциклопедия

Растяжение-сжатие — – вид деформации железобетонного элемента под дей­ствием продольных (растягивающих или сжимающих) сил. [Терминологический словарь по бетону и железобетону. ФГУП «НИЦ «Строительство» НИИЖБ им. А. А. Гвоздева, Москва, 2007 г. 110 стр.]… … Энциклопедия терминов, определений и пояснений строительных материалов

Растяжение (Деформация) — Растяжение сжатие в сопротивлении материалов вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному… … Википедия

РАСТЯЖЕНИЕ-СЖАТИЕ — в сопротивлении материалов деформация стержня под действием сил, равнодействующая которых направлена по оси центров тяжести его поперечных сечений. Силы могут быть приложены к концам стержня или распределены по его длине … Большой Энциклопедический словарь

растяжение-сжатие — (в сопротивлении материалов), деформация стержня под действием сил, равнодействующая которых направлена по оси центров тяжести его поперечных сечений. Силы могут быть приложены к концам стержня или распределены по его длине. * * * РАСТЯЖЕНИЕ… … Энциклопедический словарь

Растяжение-сжатие — У этого термина существуют и другие значения, см. Сжатие. Растяжение сжатие в сопротивлении материалов вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси… … Википедия

Растяжение-сжатие — в сопротивлении материалов, вид деформации (См. Деформация) стержня под действием сил, равнодействующая которых нормальна поперечному сечению стержня и проходит через его центр тяжести. Р. с. называется также линейное (одноосное)… … Большая советская энциклопедия

Растяжение — I Растяжение дисторсия (от лат. distortio искривление, скручивание), повреждение мягких тканей (мышц, связок, сухожилий, нервов) под влиянием силы, растягивающей их, но не нарушающей анатомической целостности ткани. Р. возникает при… … Большая советская энциклопедия

РАСТЯЖЕНИЕ-СЖАТИЕ — (в сопротивлении материалов), деформация стержня под действием сил, равнодействующая к рых направлена по оси центров тяжести его поперечных сечений. Силы могут быть приложены к концам стержня или распределены по его длине … Естествознание. Энциклопедический словарь

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ — раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность … Энциклопедия Кольера

Источник

Растяжение-сжатие.

Внутренние усилия при растяжении-сжатии.

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)

Напряжения при растяжении-сжатии.

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
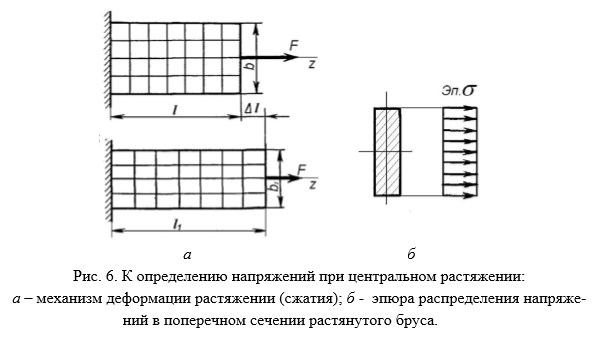
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.

Деформации при растяжении-сжатии.

Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l₁ и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

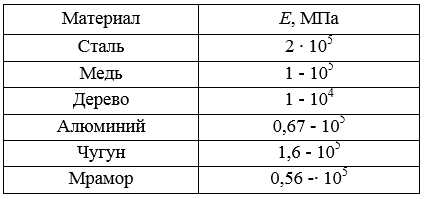
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε ‘ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε ‘ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

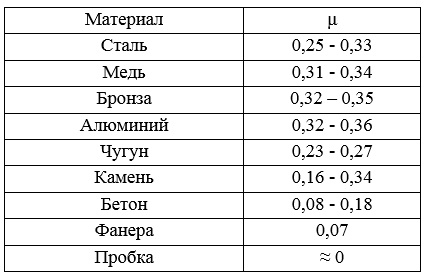
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).

Механические свойства материалов.

Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.

Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).

Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.

Твердость – свойство материала сопротивляться проникновению в него других тел.

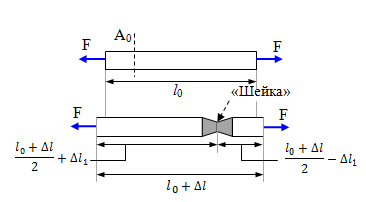
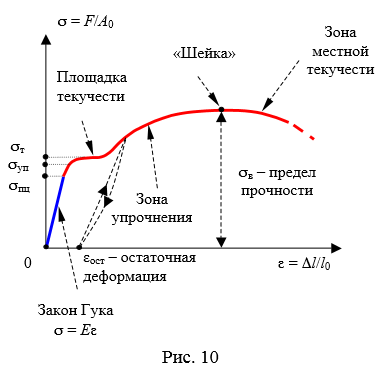
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l₀ и начальным постоянным поперечным сечением площади A₀ статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

Расчеты на прочность и жесткость при растяжении и сжатии.

Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

Расчеты на прочность при растяжении и сжатии.

Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.

Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.

Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.

Следующая важная статья теории:
Изгиб балки

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Растяжение — Сжатие

Расчеты на прочность при осевом растяжении (сжатии). Типы задач при расчете на прочность

Условие прочности при растяжении (сжатии):, где

Если расчет ведется по методу предельных состояний,то в расчет вместо допускаемого напряжения вводится расчетное сопротивление материала R.

Три типа задач при расчете на прочность при растяжении (сжатии)

1. Проверочный расчет

2. Проектный расчет или подбор сечения

3. Определение допускаемой нагрузки

Коэффициент Пуассона

Рассмотрим схему, согласно которой стержень растягивается силой Р. Ширина стержня b, длина ℓ.

Эта безразмерная величина называется относительной продольной деформацией.

Это относительная поперечная деформация.

медь, μ = 0,31 : 0,34; сталь, μ = 0,25 : 0,33; чугун, μ = 0,19 : 0,27; бетон, μ = 0,08 : 0,18

Коэффициент Пуассона характеризует физические свойства материала.

Напряжения и деформации в стержне от собственного веса

Влияние собственного веса на напряжения и деформации.В длинных вертикальных брусьях существенную роль играет собственный вес, он вызывает напряжения и деформации, которые нельзя не учитывать. Вес материала G представляет собой нагрузку, равномерно распределенную по объему бруса. Рассмотрим схему, согласно которой стержень подвергается действию собственного веса G (а).

Схема к учету собственного веса: а) общее нагружение; б) для определения напряжений; в) для определения удлинений

Проведем сечение 1 – 1 и рассмотрим равновесие отсеченной части (рис. б). В сечении 1 – 1 будет действовать неизвестное усилие от собственного веса N_G, Составим уравнение равновесия на ось z:

Определим напряжение от собственного веса:

Теперь разберемся с деформациями. Так как напряжения возрастают пропорционально расстоянию z, то и относительные удлинения бесконечно малых по длине элементов бруса dz согласно закону Гука пропорциональны величине z:

Абсолютное удлинение элемента dz составляет:

Полное удлинение всего бруса складывается из удлинений отдельных элементов:

(2)Умножим числитель и знаменатель на А:

Если сравнить формулу (3) и формулу закона Гука для деформаций: увидим, что абсолютное удлинение бруса от собственного веса равно половине того удлинения, которое получит тот же брус от силы, равной его весу и приложенной к свободному концу.

Иными словами, абсолютное удлинение от собственного веса равно удлинению, которое получит брус, если его вес будет сосредоточен в центре тяжести.

Закон Гука при растяжении – сжатии

Вывод закона Гука при растяжении – сжатии. В ходе многочисленных экспериментов установлена зависимость между нагрузкой, приложенной к стержню, и перемещениями сечений, к которым эта нагрузка приложена:

Произведение ЕА – называется жесткостью сечения стержня при растяжении – сжатии.

получаем величину относительной продольной деформации.

Тогда: Или, собственно, закон Гука при растяжении-сжатии:

Этот закон был предложен в 1660 г. английским физиком Гуком (закон был опубликован только в 1678 г.). В 1680 г. этот же закон независимо от Гука открыл французский ученый Мариотт.

Напряжения, возникающие под действием температуры

Температурные напряжения. При нагреве или охлаждении в элементах конструкций возникают напряжения. Рассмотрим стержень, защемленный с двух сторон и подвергающийся нагреву, т.е. имеем: t₂>t₁.

Схема к расчету нагретого стержня

Составим уравнение статики: Р₁ – Р₂ = 0 Как видим, задача статически неопределима.

Если мысленно снять правое защемление, то под действием усилия распора и температуры возникнут перемещения:

, где α – коэффициент линейного расширения материала. Тогда имеем:

Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения α и разности температур ∆t.

При нагреве стержня в нем возникают сжимающие напряжения при невозможности свободного удлинения (а), при охлаждении – растягивающие, поскольку брус будет испытывать растяжение, не имея возможности свободно укорачиваться (б). Вообще при изучении температурных напряжений следует строго разграничивать понятия: растяжение и удлинение, сжатие и укорочение, так как в некоторых задачах стержни могут удлиняться, испытывая при этом сжатие и наоборот.

Центральное (осевое) растяжение (сжатие) стержней

Растяжение (сжатие) – это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.

Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения, на продольную ось бруса.

Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.

Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.

Правило знаков для σ совпадает с правилом знаков для N.

В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.

Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом

ε=Δℓ/ℓ.

Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)

где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:

Значение модуля упругости устанавливается экспериментально.

Согласно закону Гука (данную запись называют законом Гука для деформаций)

Δℓ=Νℓ/ЕА

Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.

Перемещение произвольного сечения ступенчатого стержня

Относительная поперечная деформация:

ε′=Δb/b

где b – поперечный размер стержня.

Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь

μ =│ε′⁄ε│ — const,

Для твердых материалов имеет значения коэффициент Пуассона

0≤μ ≤0,5

Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tº_к-tº_н) — изменение температуры между значениями начальным (tº_н) и конечным (tº_к).

Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.

Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.

В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.

Алгоритм решения подобных задач включает следующее:

1) Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.

2) Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.

3) Физическая связь. Записываются законы деформирования отдельных стержней системы.

Порядок расчета статически неопределимых брусьев

Порядок расчета статически неопределимых шарнирно-стержневых систем

Источник