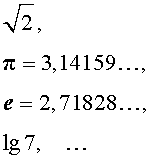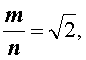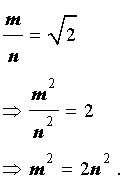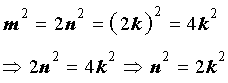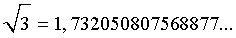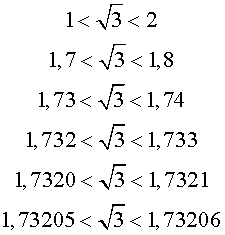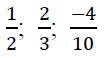Что такое рациональные числа и иррациональные числа примеры
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Понятие о вещественных (действительных) числах, рациональные и иррациональные числа
Содержание
 Рациональные и иррациональные числа. Понятие о вещественных числах Рациональные и иррациональные числа. Понятие о вещественных числах |
 Иррациональность числа Иррациональность числа 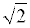 |
 Десятичные приближения иррациональных чисел с недостатком и с избытком Десятичные приближения иррациональных чисел с недостатком и с избытком |
Рациональные и иррациональные числа. Понятие о вещественных числах
Каждое из рациональных чисел можно представить в виде

где m – целое число, а n – натуральное число.
и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Иррациональность числа 
Проведем доказательство иррациональности числа 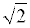
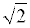

и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:
Отсюда вытекает, что число n 2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби

Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению
не существует. Следовательно, число 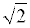
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа 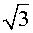
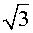
Само число 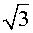
Для числа 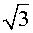
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.
Виды чисел.
У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.
Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…
Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…
Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: 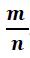
где m−целое число (числитель), n – натуральное число (знаменатель).
Например:
Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида 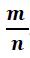
Например: √2; √5; π; e
Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:
Видно их вложенность друг в друга.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Действительные числа, рациональные числа и иррациональные числа
Вы будете перенаправлены на Автор24
В ходе изучения математики мы сталкивались с различными числами.
Натуральные числа
Противоположные числа
Если два числа отличаются только знаками, их называют в математике противоположными числами.
Для любого числа есть противоположное число, и притом только одно.
Число нуль противоположно самому себе.
Целые числа
Целыми числами называют натуральные, противоположные им числа и нуль.
Множество целых чисел включает в себя множество натуральных и противоположных им.
Дробные числа
Так же, как и целые, дробные числа могут быть как положительными, так и отрицательными.
Рациональные числа
Рациональными числами называется множество чисел, содержащее в себе множество целых и дробных чисел.
Готовые работы на аналогичную тему
Таким образом, одно и то же рациональное число можно записать разными способами.
Отсюда видно, что любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби.
В результате выполнения любого арифметического действия над рациональными числами полученный ответ будет рациональным числом. Это легко доказуемо, в силу того, что при сложении, вычитании, умножении и делении обыкновенных дробей получится обыкновенная дробь
Иррациональные числа
В ходе изучения курса математики часто приходится сталкиваться в решении с числами, которые не являются рациональными.
Такие числа называются иррациональными.
Итак, иррациональным числом называют бесконечную десятичную непериодическую дробь.
При выполнении арифметических действий с иррациональными числами получаемый результат может оказаться и рациональным, так и иррациональным числом.
Докажем это на примере нахождения произведения иррациональным чисел. Найдем:
На этом примере видно, что результат может оказаться как рациональным, так и иррациональным числом.
Действительные числа
Множеством действительных чисел называется множество содержащее множество рациональных и иррациональных чисел.
Мы говорили ранее о том, что иррациональным числом называют бесконечную десятичную непериодическую дробь, а любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби, поэтому действительным числом будет являться любая конечная и бесконечная десятичная дробь.
При выполнении алгебраических действий будут выполняться следующие правила
Также действительные числа можно сравнивать друг с другом.
Рациональное и иррациональное число: описание и чем они отличаются?
Откуда же произошли следующие термины такие, как:
А свои корни они извлекли из латинского слова «ratio», что означает «разум». Исходя из дословного перевода:
Общее понятие рационального числа
Рациональным числом считается то число, которое можно записать в виде:
Иными словами, к рациональному число подойдет следующие определения:
Примеры рационального числа
Рассмотрим примеры рациональных чисел:
Из вышеперечисленных примеров совершенно очевидно, что рациональные числа могут быть как положительными так и отрицательными. Естественно, число 0 (нуль), которое тоже в свою очередь является рациональным числом, в тоже время не относится к категории положительного или отрицательного числа.
Общее понятие и определение иррационального числа
Помимо «рациональных чисел» нам известны и так называемые «иррациональные числа». Вкратце попробуем дать определение данным числам.
Еще древние математики, желая вычислить диагональ квадрата по его сторонам, узнали о существовании иррационального числа.
Исходя из определения о рациональных числах, можно выстроить логическую цепь и дать определение иррациональному числу.
Итак, по сути, те действительные числа, которые не являются рациональными, элементарно и есть иррациональными числами.
Десятичные дроби же, выражающие иррациональные числа, не периодичны и бесконечны.
Примеры иррационального числа
Рассмотрим для наглядности небольшой пример иррационально числа. Как мы уже поняли, бесконечные десятичные непериодические дроби называются иррациональными, к примеру:
Вообще все действительные числа являются как рациональными так и иррациональными. Говоря простыми словами, иррациональное число нельзя представить ввиде обыкновенной дроби х/у.
Общее заключение и краткое сравнение между числами
Мы рассмотрели каждое число по отдельности, осталось отличие между рациональным числом и иррациональным:
Заключим нашу статью несколькими определениями: