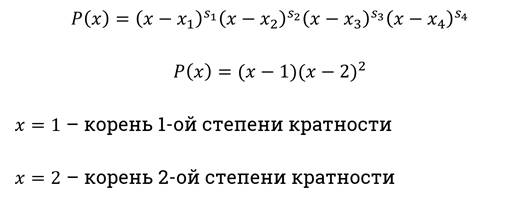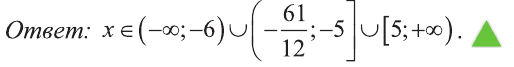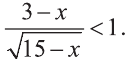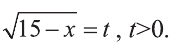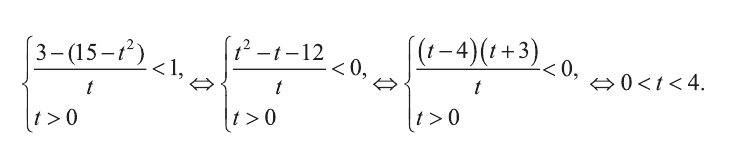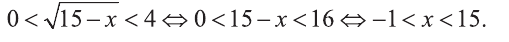Что такое рациональные неравенства определение

Рациональные неравенства (ЕГЭ 2022)

Хочешь без труда решать ЛЮБЫЕ неравенства?

Тогда начни с рациональных! Они станут твоей крепкой опорой в решении других неравенств.

Читай эту статью и ты во всём разберешься!

Рациональные неравенства — коротко о главном

Определение рационального неравенства

Рациональное неравенство — неравенство, левая и правая части которого являются дробно-рациональными функциями, то есть функциями, представимыми в виде отношения многочленов \(\displaystyle f\left(x\right)\) и \(\displaystyle g\left(x\right)\).

Стандартный вид рационального неравенства

Строгие рациональные неравенства

Рациональные неравенства — подробнее

Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.

Что такое рациональное выражение? Напомню:

Рациональное выражение — это алгебраическое выражение, составленное из чисел и переменной \(\displaystyle x\) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.

Например, такое рациональное неравенство: \(\displaystyle \frac<-2>\le \frac\)

Решение всех рациональных неравенств сводится к двум основным шагам:

Шаг 1. Перенос. Общий знаменатель. Разложение на множители

Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.

Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.

Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.

Если забыл, как раскладывать выражение на множители, прочти тему «Разложение многочленов на множители».

Шаг 2. Метод интервалов

Если не знаешь, что это такое, прочти тему «Метод интервалов».

Первый шаг у нас уже раньше встречался. Где? В рациональных уравнениях!

Но в отличие от уравнений, в неравенствах мы никогда не разделяем числитель и знаменатель!

Более того, если в числителе и знаменателе есть одинаковые нечисловые множители, мы их не сокращаем!

Это правило у нас уже было в теме «Метод интервалов». И вообще, в этой теме мы уже учились решать рациональные неравенства. Поэтому здесь ограничимся отдельными примерами.

Источник

Рациональные неравенства

Урок 29. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Рациональные неравенства»

· повторить, какие выражения называются рациональными;

· повторить как решаются рациональные неравенства методом интервалов.

Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.

Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения деления и возведения в степень с натуральным показателем.

Один из видов рациональных неравенств, а именно, линейные неравенства, мы уже повторили. На сегодняшнем уроке мы поговорим о других рациональных неравенствах.

Рациональные неравенства бывают целыми, если в них нет операции деления на выражение, содержащее переменную.

Дробно-рациональными. Это неравенства, в которых есть операция деления на выражение, содержащее переменную.

Основным методом решения рациональных неравенств является метод интервалов.

Алгоритм решения неравенств методом интервалов прост:

1. Все члены неравенства перенести в левую часть, если неравенство дробно-рациональное, то привести левую часть к общему знаменателю.

2. Найти все значения переменной, при которых числитель и знаменатель обращаются в ноль.

3. Нанести найденные точки на числовую прямую, разбивая её при этом на интервалы, в каждом из которых рациональная функция сохраняет знак.

4. Определить знак функции на любом из интервалов.

5. Определить знаки на остальных интервалах: при переходе через точку знак меняется на противоположный, если точка является корнем нечётной степени кратности (то есть встречается нечётное количество раз среди корней числителя и знаменателя); при переходе через точку четной кратности знак сохраняется.

Здесь давайте вернёмся к теме многочлен и вспомним, что такое корни чётной и нечётной степени кратности.

6. Множеством решений неравенства является объединение интервалов с соответствующим знаком функций. В случае нестрого неравенства к этому множеству добавляются корни числителя.

Рассмотрим использование этого алгоритма на примере.

Сегодня на уроке вы вспомнили какие неравенства называются рациональными. Вспомнили как решаются неравенства методом интервалов.

Источник

Рациональные неравенства

Рациональное неравенство — это неравенство, которое можно свести к виду \[\Large<\dfrac\lor 0>\] где \(P(x),\ Q(x)\) — многочлены.
( \(\lor\) — один из знаков \(\geqslant, \ \leqslant, \ >, \ )
Например, следующие неравенства являются рациональными: \[\dfrac1>0,\qquad x+2+\dfrac

Общее правило решения линейных неравенств:

Решение. I способ
Сделаем цепочку преобразований:

Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:

\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x

Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:

Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида

Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.

Существует два способа решения таких неравенств:

1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[ <\large<\left[\begin\begin &\begin P(x)\geqslant 0\\ Q(x)>0 \end\\ &\begin P(x)\leqslant 0\\ Q(x)

2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!

Итак, пусть после разложения на множители неравенство приняло вид \[\dfrac <(x+1)^3(3-x)(2-3x)^2>\geqslant0\]

Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с \(a>0\) знак неравенства остается прежним, а вот при вычеркивании скобок с \(a знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.

Таким образом, неравенство примет вид \[\dfrac <(x+1)^3(3-x)(2-3x)^2>\leqslant 0\]

Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).

В нашем неравенстве среди плохих одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\) ), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: \[\dfrac <(x+1)^3(x-3)(3x-2)^2>\geqslant0\quad (***)\]

4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.

Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.

Т.к. все скобки – хорошие, то первый знак всегда будет “ \(+\,\) ” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень \(x=3\) ), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.

Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки \(-1, \ 0, \ \dfrac23\) (например, точка \(-1\) входит в четное количество скобок: одна в числителе \((x+1)\) и три в знаменателе \((x+1)^3\) ).

Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки \(3\) и \(1\) ).

5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “ \(+\,\) ” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup \left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\] Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “ \((\) ” или “ \()\) ”, если входит в ответ – то в квадратной скобке “ \([\) ” или “ \(]\) ”. Бесконечности всегда пишутся в круглых скобках.

Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]

или сводящееся к такому виду.

Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа ( \(x\in \mathbb\) ).

Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.

Замечание

Вспомним, как преобразуется квадратичный трехчлен \(ax^2+bx+c\) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение \(ax^2+bx+c=0\)

\(\bullet\) не имеет корней ( \(D ), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю и не разлагается на линейные множители.

Шаг 2. Таким образом, наша парабола будет одного из 6 видов: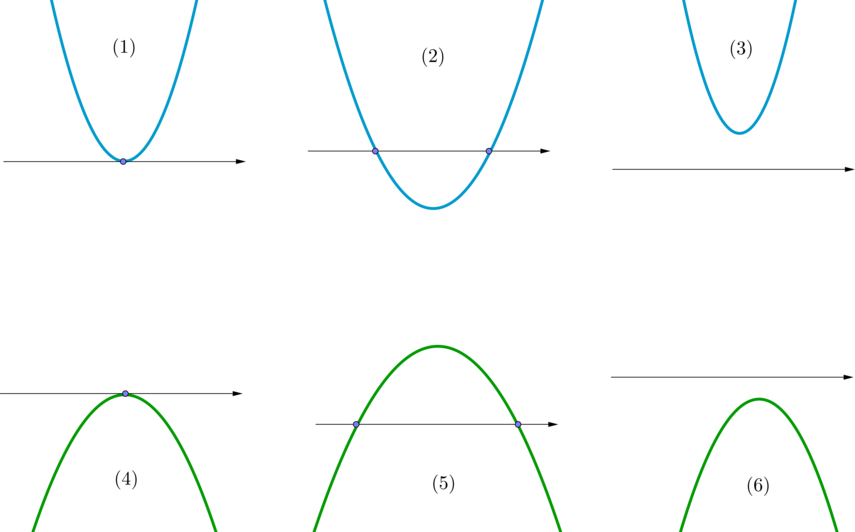
\((1)\) и \((4)\) — когда уравнение \((*)\) имеет один корень;
\((2)\) и \((5)\) — когда уравнение \((*)\) имеет два корня;
\((3)\) и \((6)\) — когда уравнение \((*)\) не имеет корней.

Пример 2.
Решить неравенство \(11x-3x^2-6>0\)

Как правило, подготовка школьников из Москвы (как и из других городов) к ЕГЭ начинается с повторения, а для кого-то и с изучения теории, например, по теме «Рациональные неравенства». Знакомство учащихся с данным разделом математики происходит в 9 классе, поэтому ничуть не удивительно, что у выпускников возникает потребность освежить в памяти правила. Если вы готовитесь к ЕГЭ, рациональные неравенства (теория) непременно стоит повторить. Сделать это вы можете, воспользовавшись нашим порталом.

«Школково» предлагает вам справочный материал, составленный нашими специалистами на основе собственного многолетнего опыта. Для того чтобы учащийся из Москвы или другого населенного пункта России, посетивший наш ресурс, смог легко и качественно подготовиться к ЕГЭ, мы в доступной форме изложили теорию по теме «Рациональные неравенства» и подобрали к ней интересные примеры с подробным описанием хода решения. После того как вы освоите материал, мы предлагаем вам закрепить его на практике. Прорешайте задания по теме, выбрав их в разделе «Каталог».

Источник

Рациональные неравенства и их системы с примерами решения

Содержание:

Простые рациональные неравенства и их системы

Рациональные неравенства одной переменной и методы их решения

Пример:

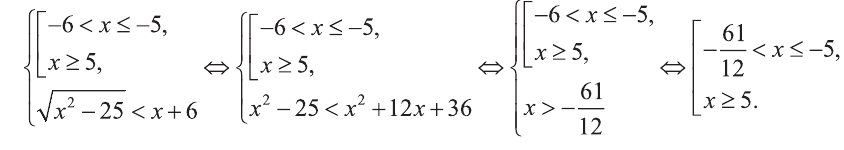
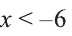
Решите неравенство: 2(2х-5)(Зх-8)(5-4х) 0, то мы можем возвести обе части заданного неравенства в квадрат: При заданное неравенства обязательно выполняется:

Замена переменной

Этот метод аналогичен соответствующему методу замены переменной, использованному при решении иррациональных уравнений.

Пример:

Решите неравенство:

Решение:

Выпишем неравенство в виде:

Введем новую переменную: 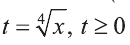В этом случае

Значит:

Пример:

Решите неравенство:

Решение:

Введем новую переменную:

Отсюда, 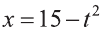и получим рациональное неравенство от переменной t:

Из последнего неравенства найдем х:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Решение целых и дробно рациональных неравенств

Продолжаем углубляться в тему «решение неравенств с одной переменной». Нам уже знакомы линейные неравенства и квадратные неравенства. Они являются частными случаями рациональных неравенств, изучением которых мы сейчас и займемся. Начнем с того, что выясним, неравенства какого вида называются рациональными. Дальше разберемся с их подразделением на целые рациональные и дробные рациональные неравенства. А уже после этого будем изучать, как проводится решение рациональных неравенств с одной переменной, запишем соответствующие алгоритмы и рассмотрим решения характерных примеров с детальными пояснениями.

Навигация по странице.

Что такое рациональные неравенства?

В школе на уроках алгебры, как только заходит разговор про решение неравенств, так сразу же и происходит встреча с рациональными неравенствами. Однако сначала их не называют своим именем, так как на этом этапе виды неравенств представляют мало интереса, а основная цель состоит в получении начальных навыков работы с неравенствами. Сам термин «рациональное неравенство» вводится позже в 9 классе, когда начинается детальное изучение неравенств именно этого вида.

Давайте узнаем, что такое рациональные неравенства. Вот определение:

Рациональное неравенство – это неравенство с переменными, обе части которого есть рациональные выражения.

В озвученном определении ничего не сказано о числе переменных, значит, допускается любое их количество. В зависимости от этого различают рациональные неравенства с одной, двумя и т.д. переменными. Кстати, в учебнике [1, c.12] дается подобное определение, но для рациональных неравенств с одной переменной. Это и понятно, так как в школе основное внимание уделяется решению неравенств с одной переменной (ниже мы тоже будем говорить лишь о решении рациональных неравенств с одной переменной). Неравенства с двумя переменными рассматривают мало, а неравенствам с тремя и большим числом переменных практически вообще не уделяют внимания.

Для удобства дальнейшего описания введем подразделение рациональных неравенств на целые и дробные.

Рациональное неравенство будем называть целым, если обе его части – целые рациональные выражения.

Дробно рациональное неравенство – это рациональное неравенство, хотя бы одна часть которого – дробное выражение.

Теперь мы имеем четкое понимание, что представляют собой рациональные неравенства, и можно смело начинать разбираться с принципами решения целых и дробно рациональных неравенств с одной переменной.

Решение целых неравенств

Поставим перед собой задачу: пусть нам надо решить целое рациональное неравенство с одной переменной x вида r(x) (знак неравенства, естественно, может быть иным ≤, >, ≥), где r(x) и s(x) – некоторые целые рациональные выражения. Для ее решения будем использовать равносильные преобразования неравенства.

В простейших случаях проделанных преобразований будет достаточно, чтобы получить искомое решение, так как они приведут нас от исходного целого рационального неравенства к неравенству, которое мы умеем решать, например, к линейному или квадратному. Рассмотрим примеры.

Получили квадратное неравенство, которое равносильно исходному неравенству. Решаем его любым известным нам методом. Проведем решение квадратного неравенства графическим способом.

Находим корни квадратного трехчлена −2·x 2 +11·x+6 :

Делаем схематический чертеж, на котором отмечаем найденные нули, и учитываем, что ветви параболы направлены вниз, так как старший коэффициент отрицательный:

Следует отметить, что иногда нецелесообразно от неравенства r(x)−s(x) (≤, >, ≥) переходить к неравенству h(x) (≤, >, ≥), где h(x) – многочлен степени выше второй. Это касается тех случаев, когда сложнее разложить многочлен h(x) на множители, чем представить выражение r(x)−s(x) в виде произведения линейных двучленов и квадратных трехчленов, например, путем вынесения за скобки общего множителя. Поясним это на примере.

Проделанное преобразование является равносильным, поэтому решение полученного неравенства будет решением и исходного неравенства.

По чертежу записываем ответ .

.

Решение дробно рациональных неравенств

Теперь займемся решением такой задачи: пусть требуется решить дробно рациональное неравенство с одной переменной x вида r(x) (≤, >, ≥), где r(x) и s(x) – некоторые рациональные выражения, причем хотя бы одно из них – дробное. Давайте сразу приведем алгоритм ее решения, после чего внесем необходимые пояснения.

Алгоритм решения дробно рационального неравенства с одной переменной r(x) (≤, >, ≥):

Так будет получено искомое решение дробно рационального неравенства.

Пояснений требует второй шаг алгоритма. Перенос выражения из правой части неравенства в левую дает неравенство r(x)−s(x) (≤, >, ≥), которое равносильно исходному. Здесь все понятно. А вот вопросы вызывает дальнейшее его преобразование к виду p(x)/q(x) (≤, >, ≥).

Первый вопрос: «Всегда ли его возможно провести»? Теоретически, да. Мы знаем, что можно любое рациональное выражение преобразовать в рациональную дробь. В числителе и знаменателе рациональной дроби находятся многочлены. А из основной теоремы алгебры и теоремы Безу следует, что любой многочлен степени n с одной переменной можно представить в виде произведения линейных двучленов. Это и объясняет возможность проведения указанного преобразования.

На практике же довольно сложно раскладывать многочлены на множители, а если их степень выше четвертой, то и не всегда возможно. Если разложение на множители невозможно, то не будет и возможности найти решение исходного неравенства, но в школе такие случаи обычно не встречаются.

Решите рациональное неравенство .

Воспользуемся алгоритмом решения рациональных неравенств.

Теперь добиваемся того, чтобы в правой части неравенства был нуль, для этого переносим выражение из правой части в левую, не забыв изменить знак этого выражения. В результате приходим к равносильному неравенству .

Дальше нужно преобразовать выражение в левой части к виду, удобному для применения метода интервалов. Сначала выполним приведение алгебраических дробей к наименьшему общему знаменателю, который очевидно есть (x−3) 2 ·(x+1) :

Еще выражение в числителе можно свернуть по формуле квадрат суммы:

Найдите решение неравенства .

Соберем все в левой части неравенства: .

Теперь преобразуем выражение в левой части неравенства. Начнем с первой дроби:

С учетом этого результата имеем

Заканчивая тему, покажем пример, в котором вывод о решении рационального неравенства делается на основе ОДЗ.

Каково решение рационального неравенства ?

Начинаем как всегда с ОДЗ, ей отвечает система . Эта система не имеет решений, так как

Таким образом, рациональное неравенство не имеет решений, так как оно не имеет смысла ни при каких значениях переменной.

Источник