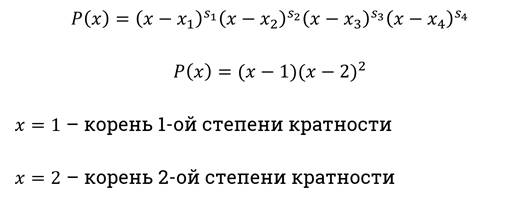Что такое рациональные неравенства
Рациональные неравенства (ЕГЭ 2022)
Хочешь без труда решать ЛЮБЫЕ неравенства?
Тогда начни с рациональных! Они станут твоей крепкой опорой в решении других неравенств.
Читай эту статью и ты во всём разберешься!
Рациональные неравенства — коротко о главном
Определение рационального неравенства
Рациональное неравенство — неравенство, левая и правая части которого являются дробно-рациональными функциями, то есть функциями, представимыми в виде отношения многочленов \(\displaystyle f\left(x\right)\) и \(\displaystyle g\left(x\right)\).
Стандартный вид рационального неравенства
Строгие рациональные неравенства
Рациональные неравенства — подробнее
Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.
Что такое рациональное выражение? Напомню:
Рациональное выражение — это алгебраическое выражение, составленное из чисел и переменной \(\displaystyle x\) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Например, такое рациональное неравенство: \(\displaystyle \frac
Решение всех рациональных неравенств сводится к двум основным шагам:
Шаг 1. Перенос. Общий знаменатель. Разложение на множители
Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.
Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.
Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.
Если забыл, как раскладывать выражение на множители, прочти тему «Разложение многочленов на множители».
Шаг 2. Метод интервалов
Если не знаешь, что это такое, прочти тему «Метод интервалов».
Первый шаг у нас уже раньше встречался. Где? В рациональных уравнениях!
Но в отличие от уравнений, в неравенствах мы никогда не разделяем числитель и знаменатель!
Более того, если в числителе и знаменателе есть одинаковые нечисловые множители, мы их не сокращаем!
Это правило у нас уже было в теме «Метод интервалов». И вообще, в этой теме мы уже учились решать рациональные неравенства. Поэтому здесь ограничимся отдельными примерами.
Рациональные неравенства
Урок 29. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Рациональные неравенства»
· повторить, какие выражения называются рациональными;
· повторить как решаются рациональные неравенства методом интервалов.
Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения деления и возведения в степень с натуральным показателем.
Один из видов рациональных неравенств, а именно, линейные неравенства, мы уже повторили. На сегодняшнем уроке мы поговорим о других рациональных неравенствах.
Рациональные неравенства бывают целыми, если в них нет операции деления на выражение, содержащее переменную.
Дробно-рациональными. Это неравенства, в которых есть операция деления на выражение, содержащее переменную.
Основным методом решения рациональных неравенств является метод интервалов.
Алгоритм решения неравенств методом интервалов прост:
1. Все члены неравенства перенести в левую часть, если неравенство дробно-рациональное, то привести левую часть к общему знаменателю.
2. Найти все значения переменной, при которых числитель и знаменатель обращаются в ноль.
3. Нанести найденные точки на числовую прямую, разбивая её при этом на интервалы, в каждом из которых рациональная функция сохраняет знак.
4. Определить знак функции на любом из интервалов.
5. Определить знаки на остальных интервалах: при переходе через точку знак меняется на противоположный, если точка является корнем нечётной степени кратности (то есть встречается нечётное количество раз среди корней числителя и знаменателя); при переходе через точку четной кратности знак сохраняется.
Здесь давайте вернёмся к теме многочлен и вспомним, что такое корни чётной и нечётной степени кратности.
6. Множеством решений неравенства является объединение интервалов с соответствующим знаком функций. В случае нестрого неравенства к этому множеству добавляются корни числителя.
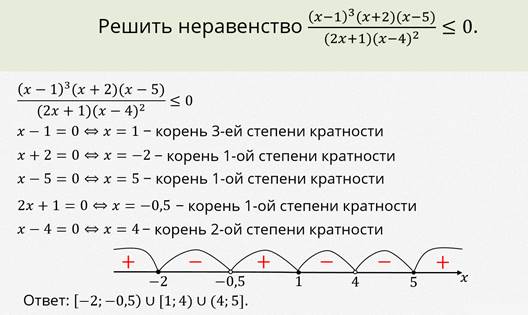
Рассмотрим использование этого алгоритма на примере.
Сегодня на уроке вы вспомнили какие неравенства называются рациональными. Вспомнили как решаются неравенства методом интервалов.