Что такое равенство фигур
Равенство и подобие геометрических фигур
Равенство геометрических фигур
Понятие равенства геометрических фигур в зависимости от принятой системы аксиом вводится по-разному. Обычно, равенства отрезков или углов определяются по их мере: два отрезка (угла) называются равными, если они имеют равные длины (величины). Затем определяются равенства треугольников, многоугольников, многогранников. Наконец, вводится понятие движения, при помощи которого понятие равенства определяется единообразно для любых геометрических фигур. В некоторых системах понятие движения (наложения, перемещения) вводится аксиоматически.
Движением (ортогональным преобразованием) называется преобразование плоскости (пространства), сохраняющее расстояние между точками, т.е. для любых двух точек и их образов имеет место равенство — расстояние между образами равно расстоянию между прообразами. Другими словами, длина отрезка является инвариантом для ортогонального преобразования. Слово «инвариант» имеет смысл «остающийся неизменным».
Подобие геометрических фигур
Отношение длин отрезков является инвариантом для преобразования подобия. В самом деле, из определения следует, что
2. Преобразования подобия и проекции относятся к так называемым аффинным преобразованиям, которые рассматриваются в разд.2.
3. В школьном курсе геометрии изучаются метрические и аффинные свойства фигур. К метрическим относятся такие свойства, которые не изменяются при ортогональных преобразованиях — преобразованиях, сохраняющих расстояния между точками, например, признаки равенства треугольников, теорема Пифагора, метрическое свойство параллелограмма, теоремы синусов и косинусов и др. К аффинным относятся свойства, которые сохраняются при преобразовании подобия (которое является частным случаем аффинного преобразования), например, признаки подобия треугольников, свойство биссектрисы треугольника, теорема Фалеса и др.
Равенство фигур
Содержимое разработки
16.01 Классная работа

В треугольнике МКР сторона МК меньше стороны КР на 18 см, а сторона МР больше стороны КР на 12 см. Найдите периметр этого треугольника, если сторона МК = 35 см
Периметр треугольника – 18 см.
Первая сторона больше второй на 4 см,
а третья больше второй на 5 см.
Найти стороны треугольника
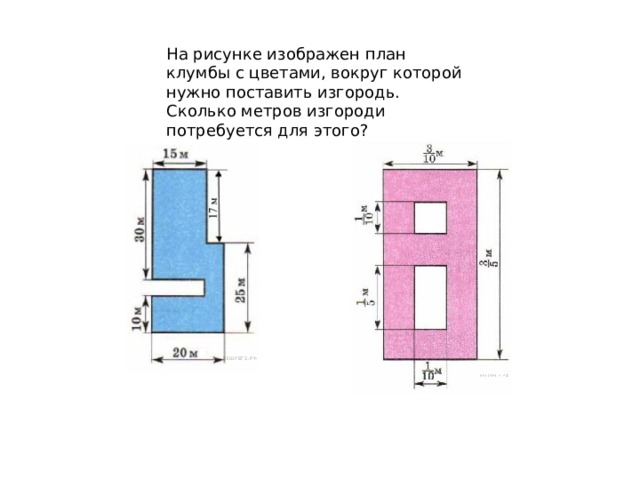
На рисунке изображен план клумбы с цветами, вокруг которой нужно поставить изгородь. Сколько метров изгороди потребуется для этого?
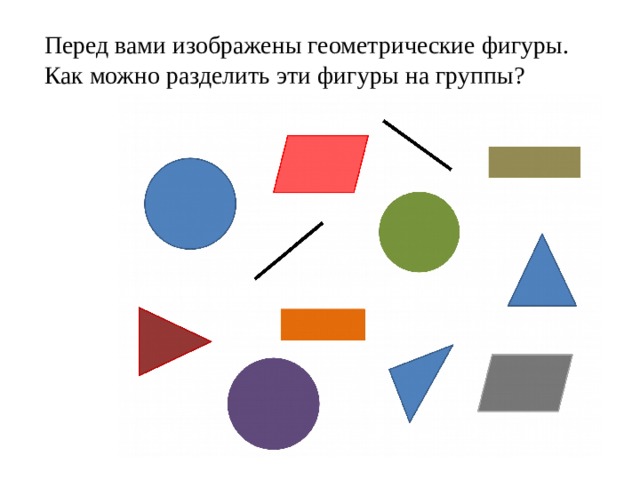
Перед вами изображены геометрические фигуры. Как можно разделить эти фигуры на группы?
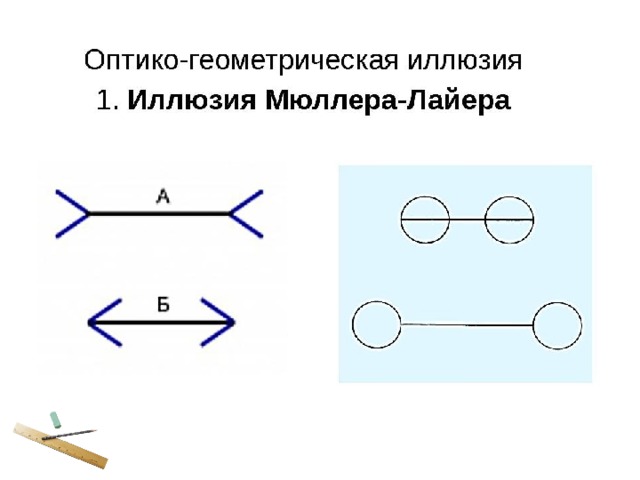
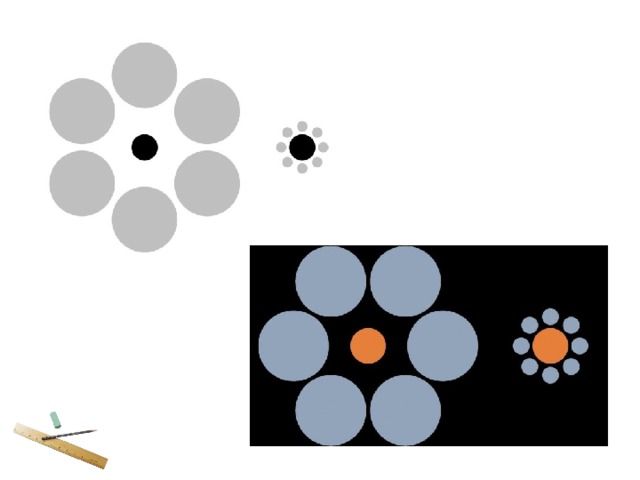
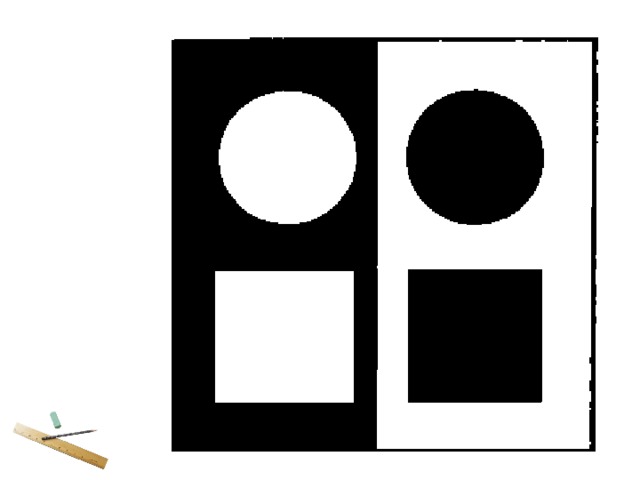
Тема урока : РАВЕНСТВО ФИГУР
Назовите равные треугольники
Ответ: А и Е ; Г и Б ; Д и В.
В равных фигурах равны все
элементы: стороны, углы
АЛГОРИТМ СРАВНЕНИЯ ФИГУР
1. Скопировать на кальку одну из фигур.
2. Наложить копию на вторую фигуру так, чтобы они совпали. При наложении кальку можно переворачивать.
3. Если фигуры совпали, то фигуры равны.
4. Если не совпали, то фигуры не равны.
Выполним практическую работу
1. Берем лист кальки. Накладываем его на многоугольник на желтом листе, обводим многоугольник и накладываем его на другой многоугольник на голубом листе. Совпали ли многоугольники? Равные они?
2. Берем ножницы и вырезаем многоугольники желтый и голубой и накладываем один на другой. Равные ли фигуры получились?
Выполняем практическую работу
из рабочей тетради №2 стр. 20 – 21
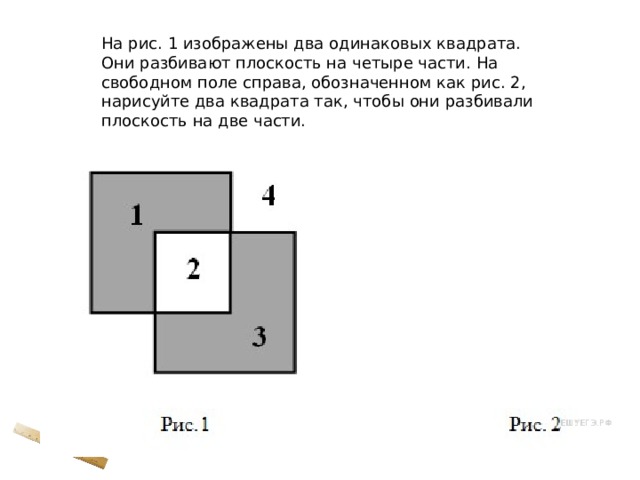
На рис. 1 изображены два одинаковых квадрата. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рис. 2, нарисуйте два квадрата так, чтобы они разбивали плоскость на две части.
У меня всё получилось!
Что – то не очень все понятно было.
Различные подходы к понятию равенства фигур
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Различные подходы к понятию равенства фигур
В «Началах» Евклида о понятии равенства говорит аксиома 7:
«И совмещающиеся друг с другом равны между собой».
Какие объекты совмещаются, и что значит «совместить», Евклид не уточнил, но можно предположить, что он имел в виду любые геометрические фигуры и те их преобразования, которые сейчас именуются движениями, перемещениями или наложениями.
О перемещениях и наложениях фигур говорил А.П.Киселев. Уже в пункте 1 своего учебника он дал такое определение:
«Две фигуры называются равными, если перемещением одной из них в пространстве ее можно совместить со второй фигурой так, что обе фигуры сливаются во всех частях».
А далее он писал следующее.
«Всякую часть плоскости можно наложить всеми ее точками на другое место этой или другой плоскости, причем накладываемую часть можно предварительно перевернуть другой стороной» (пункт 3).
«Два отрезка равны, если они могут быть наложены один на другой так, что их концы совпадут» (пункт 6).
«Два угла считаются равными, если при наложении они могут совместиться» (пункт 14).
«Две геометрические фигуры, например два треугольника, как мы знаем, называются равными, если они при наложении могут быть совмещены» (пункт 41).
Определений понятиям «наложение» и «перемещение» А.П.Киселев не дает.
К числу основных (не определяемых явно) понятий относят наложение Л.САтанасян и его соавторы, определяя с его помощью понятие равенства фигур.
«Две геометрические фигуры называются равными, если их можно совместить наложением».
Используя понятия равенства отрезков и равенства углов, в учебнике авторы на описательном уровне рассказывают об измерении отрезков и углов (§ 4 и § 5) и вводят уже в самом начале систематического курса геометрии понятия «длина отрезка» и «градусная мера угла». Такой описательный уровень изложения представляется в 7 классе разумным и единственно возможным, а откладывать на более поздний срок введение этих важнейших понятий не стоит.
В упомянутом учебнике А.П.Киселева в начале курса на описательном уровне рассказано о градусной мере угла (пункт 18). Теория измерения отрезков дается только в пунктах 144—155; она является наиболее сложным местом в книге (соизмеримые и несоизмеримые отрезки и другие тонкости этой теории мне, учившемуся по учебнику А.П.Киселева, запомнились на всю жизнь, и эти воспоминания нельзя назвать приятными).
Еще один подход предложил Д.Гильберт. В третьей группе своих аксиом — в аксиомах конгруэнтности — как основные он вводит отношения «конгруэнтность отрезков» и «конгруэнтность углов». Фигурой Гильберт называет конечную систему точек, а две фигуры называет конгруэнтными, если их точки можно попарно поставить в соответствие друг другу таким образом, чтобы отрезки и углы, оказавшиеся при этом в соответствии, были друг другу конгруэнтны.
Наконец, А.Д.Александров в монографии «Основания геометрии» при построении планиметрии за основные принимает понятия «отрезок» и «равенство отрезков», а затем, построив алгебру отрезков, применяет ее для измерения длины отрезка. В отличие от Д.Гильберта «равенство углов» А.Д.Александров к основным понятиям не относит, а определяет его через равенство отрезков. Во всех вариантах школьного учебника геометрии А.Д.Александрова и его соавторов эта линия в начале 7 класса дается описательно и завершается введением длины отрезка. Общее же понятие о равенстве фигур определяется позднее, в 9 классе: фигуры равны, если их можно совместить движением.
Какие фигуры называются равными
Содержание статьи
Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно».
Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.
Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.
Движение и равные фигуры
Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.
Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.
Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.
Равновеликие и равносоставленные фигуры
С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.
Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.
Признаки равенства треугольников
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.