Что такое равенство в геометрии

Признаки равенства треугольников

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Равенство и подобие геометрических фигур

Равенство геометрических фигур

Понятие равенства геометрических фигур в зависимости от принятой системы аксиом вводится по-разному. Обычно, равенства отрезков или углов определяются по их мере: два отрезка (угла) называются равными, если они имеют равные длины (величины). Затем определяются равенства треугольников, многоугольников, многогранников. Наконец, вводится понятие движения, при помощи которого понятие равенства определяется единообразно для любых геометрических фигур. В некоторых системах понятие движения (наложения, перемещения) вводится аксиоматически.

Движением (ортогональным преобразованием) называется преобразование плоскости (пространства), сохраняющее расстояние между точками, т.е. для любых двух точек и их образов имеет место равенство — расстояние между образами равно расстоянию между прообразами. Другими словами, длина отрезка является инвариантом для ортогонального преобразования. Слово «инвариант» имеет смысл «остающийся неизменным».

Подобие геометрических фигур

Отношение длин отрезков является инвариантом для преобразования подобия. В самом деле, из определения следует, что

2. Преобразования подобия и проекции относятся к так называемым аффинным преобразованиям, которые рассматриваются в разд.2.

3. В школьном курсе геометрии изучаются метрические и аффинные свойства фигур. К метрическим относятся такие свойства, которые не изменяются при ортогональных преобразованиях — преобразованиях, сохраняющих расстояния между точками, например, признаки равенства треугольников, теорема Пифагора, метрическое свойство параллелограмма, теоремы синусов и косинусов и др. К аффинным относятся свойства, которые сохраняются при преобразовании подобия (которое является частным случаем аффинного преобразования), например, признаки подобия треугольников, свойство биссектрисы треугольника, теорема Фалеса и др.

Источник

Равенство геометрических фигур

В повседневной жизни нас с вами окружают множество различных предметов. Часть из них имеют одинаковые размеры и одинаковую форму. Например, две одинаковые простыни или два одинаковых куска мыла, две одинаковых монеты и т.д.

В геометрии фигуры, имеющие одинаковые размеры и форму, называются равными фигурами. На рисунке ниже изображены две фигуры А1 и А2. Чтобы установить равенство этих фигур, нам необходимо одну из них скопировать на кальку. А затем передвигать кальку и совместить копию одной фигуры с другой фигурой. Если они совместятся, то это означает, что эти фигуры являются одинаковыми фигурами. При это записывают А1=А2 используя обычный знак равенства.

Определение равенства двух геометрических фигур

Мы можем представить, что на вторую фигуру накладывали первую фигуру, а не её копию на кальке. Поэтому в дальнейшем будем говорить о наложении самой фигуры, а не её копии, на другую фигуру. Исходя из всего вышесказанного можно сформулировать определение равенства двух геометрических фигур.

Две геометрические фигуры называются равными, если их можно совместить наложением одной фигуры на другую. В геометрии для некоторых геометрических фигур (например, треугольники) сформулированы специальные признаки, при выполнении которых можно говорить о том, что фигуры равны.

Источник

Равенство фигур

Содержимое разработки

16.01 Классная работа

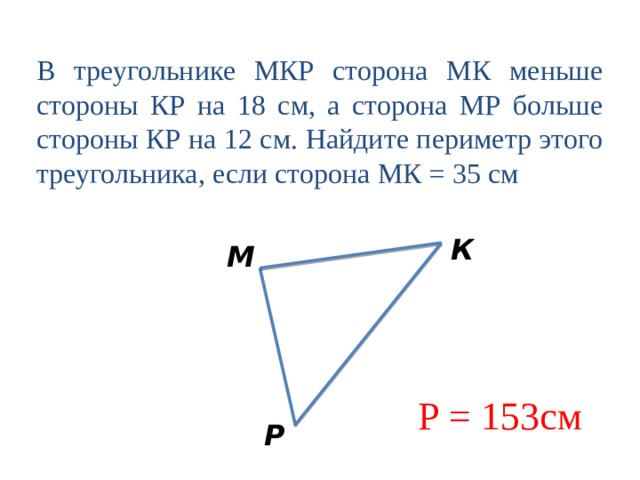
В треугольнике МКР сторона МК меньше стороны КР на 18 см, а сторона МР больше стороны КР на 12 см. Найдите периметр этого треугольника, если сторона МК = 35 см

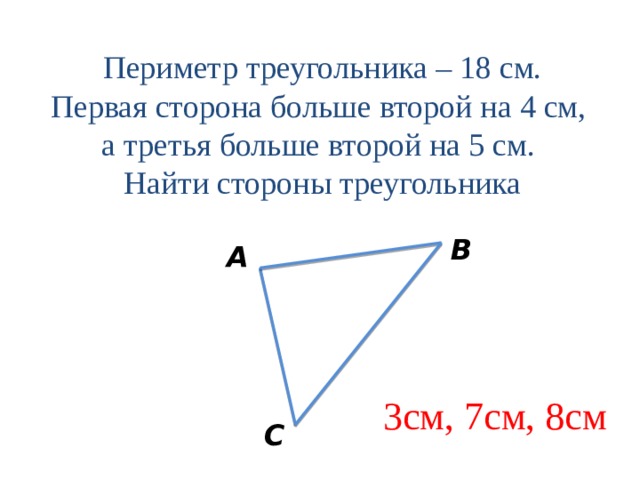
Периметр треугольника – 18 см.

Первая сторона больше второй на 4 см,

а третья больше второй на 5 см.

Найти стороны треугольника

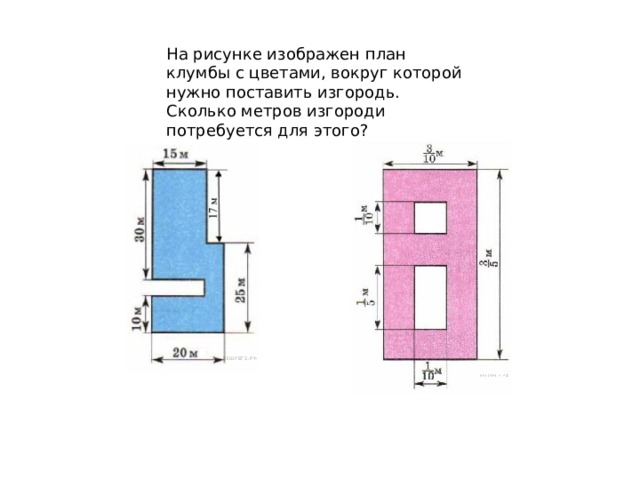
На рисунке изображен план клумбы с цветами, вокруг которой нужно поставить изгородь. Сколько метров изгороди потребуется для этого?

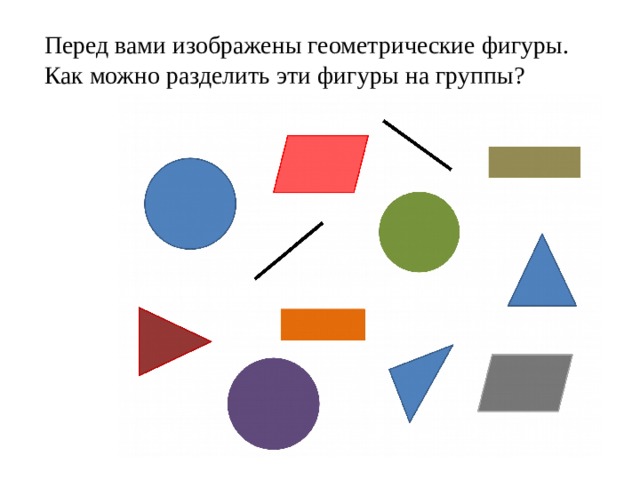
Перед вами изображены геометрические фигуры. Как можно разделить эти фигуры на группы?

Тема урока : РАВЕНСТВО ФИГУР

Назовите равные треугольники

Ответ: А и Е ; Г и Б ; Д и В.

В равных фигурах равны все

элементы: стороны, углы

АЛГОРИТМ СРАВНЕНИЯ ФИГУР

1. Скопировать на кальку одну из фигур.

2. Наложить копию на вторую фигуру так, чтобы они совпали. При наложении кальку можно переворачивать.

3. Если фигуры совпали, то фигуры равны.

4. Если не совпали, то фигуры не равны.

Выполним практическую работу

1. Берем лист кальки. Накладываем его на многоугольник на желтом листе, обводим многоугольник и накладываем его на другой многоугольник на голубом листе. Совпали ли многоугольники? Равные они?

2. Берем ножницы и вырезаем многоугольники желтый и голубой и накладываем один на другой. Равные ли фигуры получились?

Выполняем практическую работу

из рабочей тетради №2 стр. 20 – 21

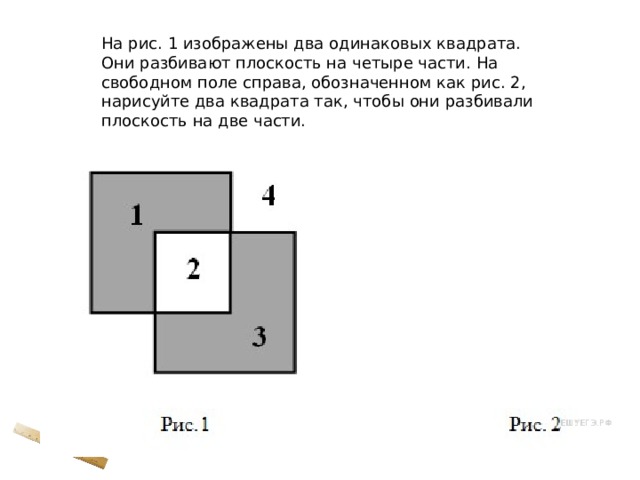
На рис. 1 изображены два одинаковых квадрата. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рис. 2, нарисуйте два квадрата так, чтобы они разбивали плоскость на две части.

У меня всё получилось!

Что – то не очень все понятно было.

Источник

Что такое равенство в геометрии

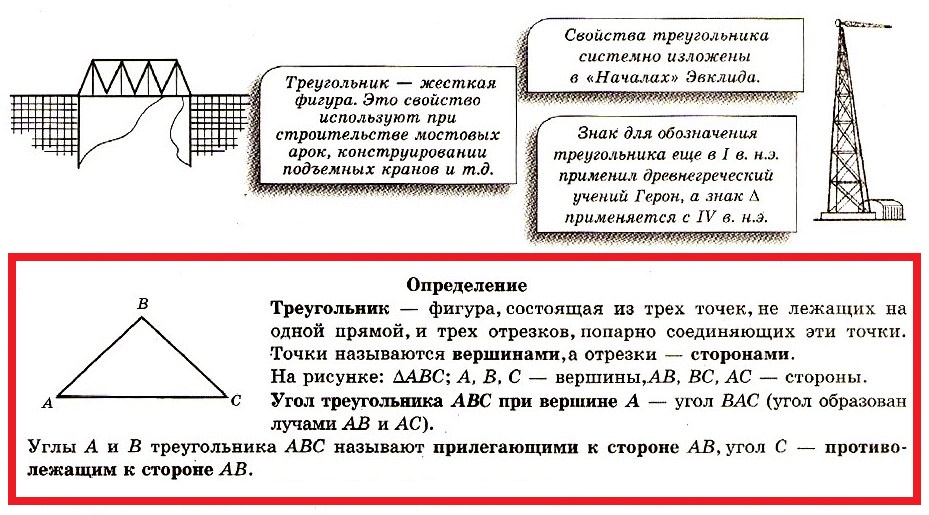
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

Источник