Что такое равнобедренная и прямоугольная трапеция

Трапеция

Трапеция — это выпуклый четырёхугольник, у которого две противолежащие стороны параллельны друг другу, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а две другие — боковыми сторонами или боками.

Отрезок, перпендикулярный основаниям трапеции, называется высотой. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией.

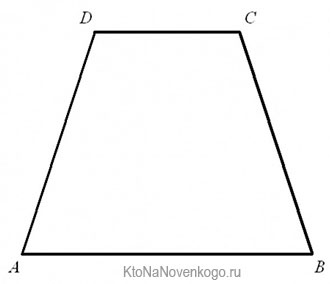
Трапеция может быть равнобедренной или прямоугольной. Равнобедренная (или равнобокая) трапеция — это трапеция, у которой боковые стороны равны. Прямоугольная трапеция — это трапеция, у которой одна из боковых сторон перпендикулярна основаниям.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Формула площади трапеции:

где S — это площадь трапеции, a и b — основания трапеции, h — высота трапеции.

Доказательство. Разделим трапецию на два треугольника, проведя диагональ BD. Получилось два треугольника ΔABD и ΔBCD, имеющих одинаковую высоту — h и основания a и b:

Площади этих треугольников будут вычисляться по следующим формулам:

Площадь трапеции будет равна сумме площадей треугольников, из которых она состоит, следовательно:

Источник

Что такое трапеция: определение, виды, свойства

В данной публикации мы рассмотрим определение, виды и свойства (касательно диагоналей, углов, средней линии, точки пересечения боковых сторон и т.д.) одной из основных геометрических фигур – трапеции.

Определение трапеции

Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.

Параллельные стороны называются основаниями трапеции (AD и BC), две другие стороны – боковыми (AB и CD).

Угол при основании трапеции – внутренний угол трапеции, образованный ее основанием и боковой стороной, например, α и β.

Трапеция записывается путем перечисления его вершин, чаще всего, это ABCD. А основаниям обозначаются маленькими латинскими буквами, например, a и b.

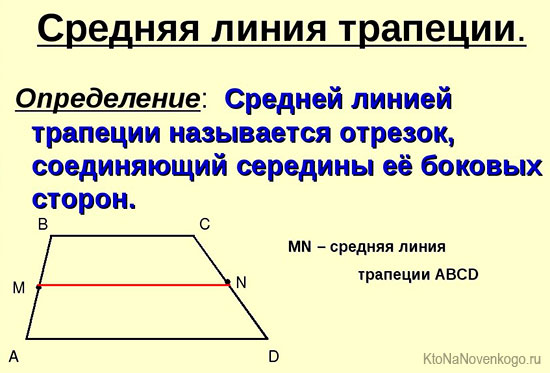
Средняя линия трапеции (MN) – отрезок, соединяющий середины ее боковых сторон.

Высота трапеции (h или BK) – это перпендикуляр, проведенный от одного основания к другому.

Виды трапеций

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной (или равнобокой).

Прямоугольная трапеция

Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.

Разносторонняя трапеция

Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.

Свойства трапеции

Перечисленные ниже свойства применимы к любым видам трапеций. Свойства равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.

Свойство 1

Сумма углов трапеции, прилежащих к одной и той же боковой стороне, равна 180°.

Свойство 2

Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.

Свойство 3

Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.

Свойство 4

Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой.

Если сумма углов при одном основании равняется 90° (т.е. ∠DAB + ∠ADC = 90°), значит продолжения боковых сторон трапеции пересекаются под прямым углом, а отрезок, который соединяет середины оснований (ML) равняется половине их разности.

Свойство 5

Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади.

Свойство 6

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований:

Свойство 7

Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны.

Свойство 8

В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.

Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.

Источник

Трапеция – это стол, который стал геометрической фигурой

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы решили подробно рассказать о такой геометрической фигуре, как ТРАПЕЦИЯ.

Ее подробно изучают на уроках геометрии в 8-м классе. И эти уроки являются частью общего знакомства школьников с различными четырехугольниками.

Определение трапеции

Трапеция – геометрическая фигура, которая представляет собой четырехугольник, у которого две противоположные стороны располагаются на параллельных прямых. А две другие стороны должны, наоборот, быть не параллельными.

Вот так выглядит классическая трапеция:

У этой фигуры стороны АВ и CD являются параллельными. А вот AD и CB – нет.

Происхождения слова

Первое упоминание об этой фигуре встречается еще в трудах известного древнегреческого математика Евклида.

В его книге «Начала» этим термином описывается абсолютно любой четырехугольник, который не является параллелограммом.

Если кто не помнит, параллелограммом называют четырехугольник, у которого противоположные стороны параллельны. Выглядит эта фигура в классическом понимании вот так:

Интересно, что и всем известные фигуры – квадрат, прямоугольник (что это?) и ромб (это как?) – также являются частным случаем параллелограмма. Ведь действительно – у них противоположные стороны параллельны друг к другу.

И получается, что Евклид был в целом прав. Он просто поделил все четырехугольники на две большие категории – параллелограммы и трапеции.

Кстати, само слово ТРАПЕЦИЯ также имеет греческое происхождение. В древние времена оно звучало как «трапедзион». И в переводе это означает « обеденный стол». Поэтому слово «трапеза», которое у нас является синонимом любого приема пищи тоже родом оттуда.

Стороны трапеции

Парные стороны трапеций имеют свои названия:

Закрепим это с помощью рисунка:

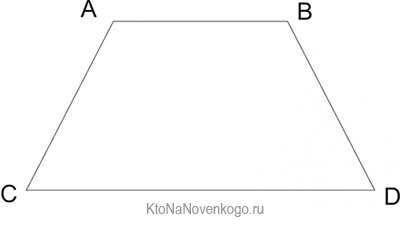
В данном случае стороны АВ и CD параллельны друг другу. А значит, именно они являются основаниями. А вот АС и BD – наоборот, явно не параллельны. И соответственно, это боковые стороны.

Кстати, расположение сторон не зависит от расположения самой фигуры. Даже вот в таких положениях

все равно параллельные стороны будут считаться основаниями, а непараллельные – боковыми.

Равнобедренная и прямоугольная трапеции

Вариант трапеции, который мы рассмотрели – это самые распространенные виды геометрической фигуры. Но есть и частные случаи:

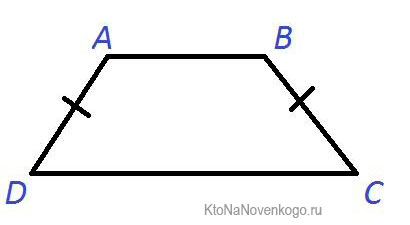
Равнобедренная трапеция – та, у которой боковые (не параллельные) стороны равны. Ее еще называют равнобокой или равнобочной.

Выглядит она вот так:

В данном примере графически показано, что стороны AD и ВС равны между собой. Об этом свидетельствуют небольшие черточки.

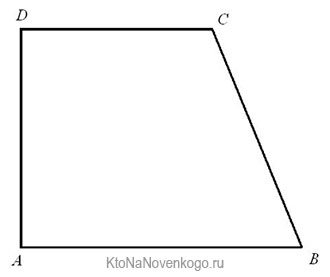
Прямоугольная трапеция – та, у которой одна из боковых сторон и основания образовывают прямой угол.

Выглядит она вот так:

В данном примере, углы DAB и ADC являются прямыми, то есть равны 90 градусам. А соответственно, трапеция называется прямоугольной.

Тут важно заметить, что под прямым углом к основанию должна идти только одна боковая сторона. Если будут обе, то трапеция автоматически превратится в квадрат.

Свойства трапеций

С трапециями связаны несколько понятий в геометрии, которые активно используются для решения различных теорем.

Средняя линия

Средняя линия трапеции – это отрезок, который идет параллельно основаниям и соединяет середины:

Со средней линией связана одна интересная теорема. Очень часто на уроках геометрии школьников просят определить ее длину. И сделать это весьма просто.

Длина средней линии трапеции равна половине суммы длин ее оснований.

Звучит может и несколько тяжеловато. Но на деле – это весьма просто. Так, чтобы посчитать в нашем примере длину отрезка MN, который является средней линией, надо применить формулу:

И это правило распространяется на все виды трапеций.

Биссектриса углов трапеции

Биссектриса – это линия (луч), которая делит угол пополам. Так вот

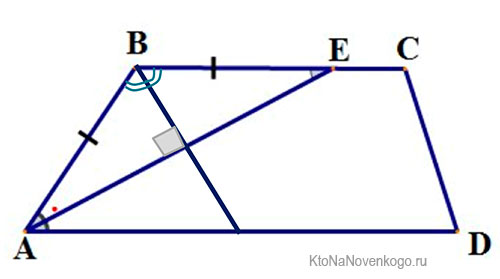
Любая биссектриса, выведенная из угла трапеции, отсекает на основании отрезок, равный по длине боковой стороне.

На данном рисунке отрезок АЕ является биссектрисой угла ABD. И исходя из этого, отрезки АВ и ВЕ равны между собой, о чем свидетельствуют небольшие черточки на них.
В то же время у биссектрис в трапеции есть еще одно свойство.

Две биссектрисы, выведенные из углов одной боковой стороны, пересекаются под прямым углом.

Все эти теоремы в процессе школьного обучения, ученикам еще необходимо доказывать. Ну а мы решили не приводить долгие математические и геометрические выкладки. Просто примите как данность!

Вот и все, что мы хотели рассказать вам о трапеции.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

А я, глядя на трапецию, пуделя своего вспомнил, о трапеции он ничего не знал, но вставал в такую стойку, что передние и задние лапы образовывали трапецию.

Источник

Трапеция

Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.

Элементы трапеции

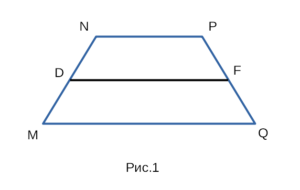
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.

В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.

Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.

Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.

Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.

Виды трапеции

Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.

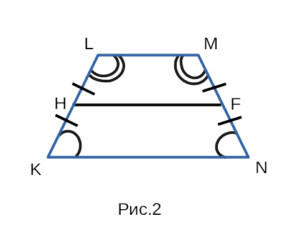
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.

В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.

В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Трапеция

Рассмотрим четырехуг-к, у которого параллельны только две стороны, а две оставшиеся не параллельны. Такая фигура именуется трапецией.

На рисунке трапеция выглядит следующим образом:

Параллельные стороны именуются основаниями трапеции, а другие две – это боковые стороны.

Обратите особое внимание на то, что одно из оснований всегда больше второго основания. Действительно, если бы основания имели одинаковую длину, то получился бы четырехуг-к, у которого две противоположные стороны и равны, и параллельны. Однако это уже один из признаков параллелограмма, а параллелограмм никак не может быть трапецией.

Иногда полезно представлять трапецию как усеченный треуг-к. Действительно, если в треугольнике провести линию, параллельную одной из сторон и пересекающую две остальные стороны, то она как бы «отсечет» верхушку этого треуг-ка, и получится трапеция. И наоборот, любую заданную трапецию можно достроить до треугольника:

Сумма всех 4 углов трапеции составляет, как и у любого четырехугольника, 360°.

Задание. Известно, что у трапеции АВСD АD||ВС, ∠А = 36°, ∠С = 117°. Найдите∠В и ∠D.

Решение: АВ можно рассматривать как секущую параллельных прямых ВС и АD. Но тогда∠А и ∠В будут являться односторонними, а их сумма будет равна 180°. Отсюда можно найти ∠В:

Аналогично, рассматривая в качестве секущей СD, можно найти и ∠D, который вместе с∠С является односторонним:

Средняя линия трапеции

Если отметить середину каждой из боковых сторон трапеции, а потом соединить эти середины, то получится отрезок, именуемый средней линией трапеции.

Докажем важную теорему, связанную со средней линией:

Для этого изучим трапецию АВСD, у которой боковые стороны – это АВ и CD. Пусть М – середина АВ. Проведем через М прямую, параллельную основаниям, которая пересечет СD в точке N. По теореме Фалеса параллельные друг другу прямые АD, МN и ВС отсекут на прямой СD равные отрезки, то есть СN = ND. Но это означает, что N– середина CD, а тогда MN – средняя линия (согласно ее определению). Естественно, что в трапеции возможно построить только одну среднюю линию, а значит, средняя линия МN параллельна каждому из оснований.

Прямоугольная и равнобедренная трапеция

Существует два частных вида трапеции, обладающих особыми свойствами. Первый из них – это прямоугольная трапеция. Она отличается тем, что один из ее углов равен 90°.

Здесь∠А = 90°. Легко догадаться, что на самом деле если у трапеции хоть один угол составляет 90°, то найдется и ещё один угол, также равный 90°. В данном случае это ∠В. Сумма ∠A и ∠D должна составлять 180°, ведь они односторонние. Именно поэтому из условия

Задание. Основания прямоугольной трапеции имеют длину 10 и 15 см, а один из углов составляет 45°. Вычислите длину ее наименьшей боковой стороны?

Пусть основания заданной трапеции – это отрезки АD и ВС, ∠А = 45°, ∠D = ∠C = 90°. Опустим из точки В перпендикуляр ВН на АD:

Очевидно, что ВН||CD, ведь эти отрезки перпендикулярны одной прямой АD. Получается, что в четырехуг-ке НВСD противоположные стороны попарно параллельны, то есть он является параллелограммом. Отсюда вытекает равенство его сторон:

Нашли СD, но является ли этот отрезок именно меньшей боковой стороной трапеции? Для ответа на этот вопрос вернемся к ∆АВН. В нем АВ – это гипотенуза, а потому она заведомо больше катета ВН, то есть больше 5 см. Значит, именно CD – это меньшая боковая сторона.

Ещё один особый вид трапеции – равнобедренная трапеция. Она отличается тем, что у неё длины боковых сторон одинаковы.

Равнобедренная трапеция обладает рядом интересных свойств. Начнем с того, что углы при каждом из ее оснований равны.

В итоге мы получили четырехуг-к АВСН, в котором АВ||CН, ВС||АН. Это значит, что он является параллелограммом, и тогда

Отсюда сразу же вытекает и второе свойство равнобедренной трапеции – у неё равные диагонали.

Действительно, треуг-ки ∆АВD и ∆АСD равны, ведь

Оказывается, есть признаки, которые позволяют определить, является ли трапеция равнобедренной. Сформулируем первый из них:

Для доказательства снова построим в трапеции АВСD такую прямую СН, что СН||АВ:

Несколько сложнее доказать другую теорему:

Пусть в трапеции АВCD одинаковы диагонали ВD и АС. Для определенности будем считать, что большее основание – это АD. Опустим из точек В и С перпендикуляры ВЕ и СF на АD:

Ясно, что эти перпендикуляры параллельны друг другу, ведь они перпендикулярны третьей прямой. Тогда в ВСFЕ противоположные стороны параллельны, то есть эта фигура – параллелограмм. Отсюда вытекает, что

Далее рассмотрим ∆ВЕD и ∆АСF. Они оба являются прямоугольными, у них одинаковы гипотенузы (АС = ВD), а также и катеты ВЕ и СF. Значит, эти треуг-ки равны, следовательно,

Задание. Один из углов равнобедренной трапеции составляет 55°. Найдите все остальные углы этой трапеции.

Решение. Проще всего найти ∠D, ведь углы при основании равнобедренной трапеции одинаковы:

Заметим одно важное обстоятельство. Если достроить равнобедренную трапецию до треугольника, продолжив ее боковые стороны, то получится равнобедренный треуг-к:

Действительно, если АВСD – равнобедренная трапеция, то

Пусть продолжения боковых сторон пересеклись в некоторой точке Е. Тогда в ∆АЕD два угла, ∠А и ∠D, окажутся равными, следовательно, ∆АЕD– равнобедренный.

Прямоугольник

Следующим особым четырехугольником является прямоугольник (иногда его сокращенно обозначают как прямоуг-к). Его отличительный признак заключается в том, что все его углы – прямые.

Продемонстрируем несколько прямоугольников:

Очевидно, что у прямоуг-ка противоположные стороны параллельны, ведь они перпендикулярны одной и той же прямой. Следовательно, всякий прямоуг-к одновременно является параллелограммом и обладает всеми его свойствами. Стоит особо отметить, что обратное утверждение неверно – отнюдь не всякий параллелограмм является прямоугольником. Другими словами, прямоугольник – это частный случай параллелограмма, который отличается тем, что его углы составляют 90°.

Из этого вытекает два свойства прямоугольника:

Однако есть ещё одно свойство, которое НЕ характерно для остальных параллелограммов.

Доказать это очень просто. Пусть есть прямоугольник АВCD:

Сравним ∆АВD и ∆АСD. Они являются прямоугольными, у них есть общий катет АD, а два других катете, АВ и СD, равны как противоположные стороны прямоугольника. Получается, что рассматриваемые треуг-ники равны, и поэтому равны и их гипотенузы, которые как раз и являются диагоналями прямоугольника.

Оказывается, верна и обратная теорема, которую называют признаком прямоугольника:

Действительно, пусть есть некоторый параллелограмм АВCD, у которого одинаковы диагонали АС и BD.

Противоположные стороны в одном параллелограмме одинаковы:

В итоге все углы АВСD оказываются прямыми, и эта фигура по определению оказывается прямоуг-ком.

Задание. В прямоуг-ке ABCD проведена биссектриса, которая делит сторону СD на отрезки СК и КD длиной 27 и 45 см соответственно. Найдите периметр АВCD.

Решение.Для нахождения периметра необходимо найти длины всех сторон.

Если АК – биссектриса, то

∆КАD является прямоугольным, и мы только что нашли один из его острых углов. Тогда можно найти и 2-ой угол:

Получается, что в ∆АКD два угла равны 45°, значит, он является равнобедренным, и

Мы нашли две смежные стороны прямоугольника, АD и СD. Две другие стороны будут им равны:

Следующая особенная фигура – это ромб. Дадим определение ромба:

На рисунке видно, что ромб похож на параллелограмм, и это не случайно. Докажем, что любой ромб является частным случаем параллелограмма. Но прежде заметим, что обратное утверждение неверно – отнюдь не каждый параллелограмм является ромбом.

Для доказательства этого факта проведем диагональ ромба:

В результате получилось два треуг-ка: ∆АВС и ∆АСD. Можно заметить два факта. Во-первых, каждый из этих треуг-ков – равнобедренный, ведь стороны ромба равны. Тогда можно записать равенство углов:

Из равенства треуг-ков вытекает и равенство углов:

Тогда очевидно, что ∠А и ∠С также равны, ведь они состоят из двух равных углов:

В итоге получается, что в ромбе противоположные углы одинаковы. Зная, что все 4 угла в сумме дают 360°, легко найдем сумму каких-нибудь двух смежных углов:

Итак, сумма смежных углов в ромбе равна 180°. Но эти углы можно рассматривать как односторонние. Если их сумма равна 180°, то и соответствующие прямые (в частности, ВС и АD) параллельны. Аналогично доказывается и то, что АВ||CD. Это и значит, что АВСD– параллелограмм.

Продолжим рассматривать построенный нами рисунок, но добавим в него ещё одну диагональ:

Во-первых, мы уже доказали следующее равенство

Из него вытекает, что диагональ АС является биссектрисой для∠А и ∠С. Аналогично и для диагонали ВD можно показать, что и она разбивает ∠В и ∠D пополам. Можно сформулировать следующее свойство ромба:

Далее рассмотрим ∆АВD. Он равнобедренный, а АО является биссектрисой, падающей на основание ВD. Но в равнобедренном треуг-ке такая биссектриса одновременно является высотой, то есть

Получается, что диагонали всякого ромба обязательно пересекаются под прямым углом.

Задание. Длина стороны ромба совпадает с длиной одной из его диагоналей. Определите углы этого ромба.

Решение. Построим рисунок по условию задачи:

Легко заметить, что∆АВС и ∆АСD будут равносторонними. Однако все углы равностороннего треуг-ка равны 60°:

Итак, два угла ромба будут равны 60°, а другие два 120°.

Квадрат

Последний особый случай четырехугольника – это квадрат. Эта фигура, которая сразу является и прямоугольником, и ромбом. Естественно, что любой квадрат одновременно является параллелограммом. Дадим определение квадрата:

Свойства квадрата – это совокупность свойств параллелограмма, ромба и прямоуг-ка.Это значит, что его диагонали:

Задание. Середины сторон квадрата соединили отрезками. Докажите, что получившаяся фигура также является квадратом.

Решение. Требуется доказать, что фигура, показанная красным цветом, является квадратом:

Так как стороны квадрата одинаковы, то одинаковы и их половины:

Получается, что ∆АМН, ∆МВР, ∆РСК и ∆КНD – прямоугольные, причем у них равны все катеты. Это значит, что, с одной стороны, они являются равнобедренными треуг-ками, а с другой стороны, они равны друг другу. Мы уже знаем, что у равнобедренного прямоугольного треуг-ка углы при основании составляют по 45°, а из равенства треуг-ков вытекает, что

Получается, что у четырехуг-ка МРКН все стороны одинаковы, то есть он является ромбом. Осталось доказать, что все его углы прямые. Рассмотрим, например, ∠РМН. Он в сумме с ∠ВМР и ∠АМН дает 180°, что позволяет вычислить его:

Итак, все углы ромба МРКН прямые, значит, он является квадратом.

Мы видим, что есть множество видов четырехугольников, причем часто одна и та же фигура может относиться сразу к нескольким типам. Для наглядности покажем на одной картинке всю иерархию четырехугольников. Здесь на одном рисунке можно увидеть название всех видов четырехугольников, их форму, также главное свойство, по которым их и определяют:

Симметрия

В заключение рассмотрим также такое важное геометрическое понятие, как симметрия.

В случае, показанном на рисунке,А₁ и А₂ не лежат на b. Если же рассматривается точка, лежащая на b, то она считается симметричной самой себе. На рисунке пары точек А и B, C и D, M и N симметричны относительно b.Для точки же Р нельзя найти парную ей симметричную точку. Поэтому условно считается, что она симметрична сама себе.

Теперь перейдем к такому понятию, как симметричная фигура.

В качестве иллюстрации приведем равнобедренный треуг-к. У него роль оси симметрии играет медиана, проведенная к основанию. Выберем на треугольнике произвольные точки А₁, В₁, С₁ и D₁. Далее отметим симметричные им относительно b точки, которые обозначим как А₂, В₂, С₂ и D₂. Видно, что они также принадлежат треугольнику:

Рассмотрим для иллюстрации и какую-нибудь несимметричную фигуру, например, треугольник с 3 разными сторонами:

Видно, что например, для точка А₁ симметричная ей А₂ НЕ принадлежит треугольнику, поэтому красная линия НЕ является осью симметрии.

Осевая симметрия присуща и многим другим фигурам:

Обратите внимание, что осей симметрии фигуры может быть несколько. У ромба их две (это его диагонали), у квадрата уже четыре (помимо диагоналей добавляются ещё и линии, соединяющие середины его противоположных сторон), а у окружности их и вовсе бесконечно много, так как любой ее диаметр может играть эту роль.

Возможен ещё один случай симметрии:

На приведенном рисунке С – это середина АВ, поэтому А и В симметричны, а точка С для них является центром симметрии.

Снова перейдем от отдельных точек к фигурам.

В частности, центральная симметрия присуща параллелограмму (его центром симметрии будет точка, в которой пересекаются его диагонали), а также окружность. Есть центральная симметрия и у любой прямой, причем в качестве центра симметрии фигуры можно выбрать любую точку, принадлежащую этой прямой:

Симметрия – это не просто умозрительная геометрическая конструкция, она встречается и в реальной жизни. Например, листья многих деревьев обладают осевой симметрией, а зубчатое колесо – центральной симметрией. Интересно, что из 32 выделяемых в царстве животных типов у представителей 28 (это более 99% известных видов) можно выделить правую и левую половину, которые симметричны друг другу. Архитекторы и конструктора при проектировании зданий и машин стремятся придать им симметричную форму, так как в большинстве случаев именно такая форма оказывается оптимальной и экономичной.

Источник