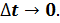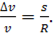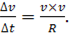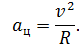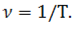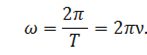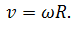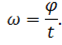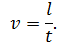Что такое равномерное движение по окружности

Равномерное движение по окружности.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Угловая скорость.

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1 ).

Рис. 1. Равномерное движение по окружности

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

Закон движения.

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

Центростремительное ускорение.

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5) :

С учётом формул (5) имеем:

Полученные формулы (6) можно записать в виде одного векторного равенства:

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1 ). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

Выразим угловую скорость из (4)

Источник

Равномерное движение точки по окружности

Урок 11. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Равномерное движение точки по окружности»

Движение тела по окружности довольно часто встречается в повседневной жизни. Взять хотя бы движение Земли вокруг своей оси или вокруг Солнца.

Кроме этого существуют ещё сотни примеров: вращение колеса автомобиля, вращение электронов вокруг ядра атома, движение стрелок часов и многое другое.

В первую очередь, давайте условимся, что называется равномерным движением по окружности? При прямолинейном движении мы говорили о том, что тело совершает одинаковые перемещения за равные промежутки времени. В случае с движением тела по окружности, равномерным движением называется такое движение, при котором тело поворачивается на одинаковые углы за равные промежутки времени.

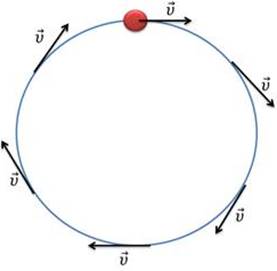
Мы уже говорили о том, что мгновенная скорость направлена по касательной к траектории движения. Значит, при движении тела по окружности, его скорость будет направлена по касательной к этой окружности в данной точке. При этом, модуль скорости, так же, как и модуль ускорения остаётся постоянным, в то время как их направления постоянно меняются.

Из этого можно сделать вывод, что любое криволинейное движение является ускоренным, даже если модуль скорости остаётся постоянным.

Давайте рассмотрим ускорение при движении тела по кривой. Поскольку направление ускорения постоянно меняется, имеет смысл рассматривать мгновенное ускорение. Точно так же, как и в случае с мгновенной скоростью, мы будем брать все меньшие и меньшие промежутки времени.

Тогда, можем записать, что мгновенное ускорение — отношение изменения скорости к промежутку времени, за который это изменение произошло, при

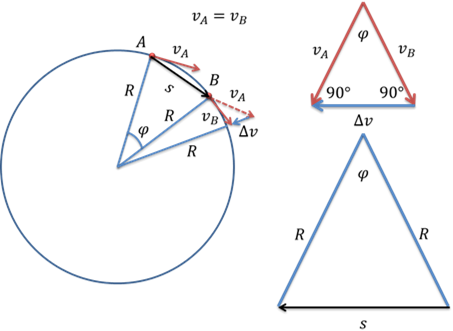
Возьмём две произвольные точки А и В, принадлежащие окружности. В обеих точках скорость будет направлена по касательной, а модуль скорости в точке A будет равен модулю скорости в точке B.

Воспользуемся теперь сложением скоростей, чтобы найти вектор показывающий направление изменения скорости. Рассмотрим два треугольника, показанные на рисунке. Один из этих треугольников образован двумя радиусами и вектором перемещения, а второй — двумя модулями скорости и вектором изменения скорости. Эти треугольники подобны, т.к. являются равнобедренными и имеют одинаковый угол при вершине. Напомним, что мы рассматриваем промежуток времени, стремящийся к нулю. В этом случае, угол поворота будет стремиться к нулю, а значит и угол между скоростью в точке A и скоростью в точке B — тоже будет стремиться к нулю.

Теперь разберёмся с модулем ускорения. Мы снова используем те же два треугольника. Поскольку треугольники подобны, мы можем записать, что

Перемещение мы можем записать как произведение скорости и времени:

Теперь преобразуем выражение:

Это, как раз, и будет модулем ускорения:

Таким образом, мы выяснили, что ускорение при движении по окружности направлено к центру и численно равно отношению квадрата скорости к радиусу окружности.

В завершении темы, вспомним несколько важных физических величин, описывающих криволинейное движение. В первую очередь, это, конечно, период обращения. Периодом обращения называется время, за которое тело совершает полный оборот.

Например, период обращения Земли вокруг Солнца равен одному году.

Существует также величина, обратная периоду, которая называется частотой. Эта величина равна числу оборотов в единицу времени. Очевидно, что период обращения и частота обратно пропорциональны:

К примеру, чем быстрее вращаются лопасти вентилятора, тем больше он оборотов совершит в единицу времени и тем меньше период обращения.

Еще одной важной характеристикой движения по окружности является угловая скорость. Скорость, о которой мы говорили до этого — это фактическая скорость движения, которая называется линейной.

Угловая скорость характеризует скорость поворота, то есть изменение угла поворота в единицу времени.

Таким образом, угловая скорость измеряется в радианах в секунду:

.

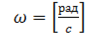
Напомним, что радиан — это угол между двумя радиусами окружности, вырезающими на окружности дугу, длина которой равна радиусу окружности. Применительно к физике, мы можем сказать, что радиан — это такой угол, при повороте на который, точка проходит путь, равный радиусу окружности.

Мы знаем, что полный оборот — это поворот на угол, равный 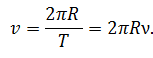. Тогда, угловая скорость будет равна:

Линейная скорость будет определяться:

Также можно записать, что линейная скорость равна произведению угловой скорости и радиуса окружности:

Это вполне логично: чем дальше точка находится от центра, вокруг которого она вращается, тем больше должна быть её линейная скорость, чтобы за одинаковое время совершить поворот на одинаковый угол.

Мы рассмотрели частный случай: когда точка совершает полный оборот по окружности. В более общем случае, угловая скорость будет определяться как отношение угла поворота ко времени, за который этот поворот был совершён:

Аналогично, линейная скорость определяется как отношение длины пройденной дуги ко времени:

Для примера рассмотрим, так называемый, геостационарный спутник. Это искусственный спутник Земли, который постоянно находится над одной и той же точкой поверхности Земли (с помощью таких спутников работает спутниковое телевидение, к примеру). Для выполнения этого условия необходимо, чтобы спутник вращался с той же угловой скоростью, что и Земля.

Пример решения задачи.

Задача. Спидометр автомобиля показывает 90 км/ч, а тахометр — 2400 об/мин. Чему равен радиус колеса в таком случае?

Источник

Физика. 10 класс

Конспект урока

Урок 04.Равномерное движение точки по окружности

Перечень вопросов, рассматриваемых на уроке:

Криволинейное движение – это движение по дугам окружностей разных радиусов.

Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0

Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56

Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.

Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.

При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.

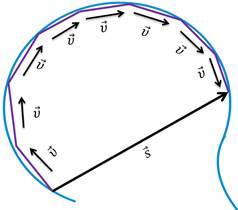
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.

Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.

Векторы и не лежат на одной прямой, угол между ними не равен нулю.

Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.

2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.

Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.

Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.

Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была_.

Модули скоростей равны:

но вектора скоростей не равны.

Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.

направлен в сторону.

Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.

Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.

Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 90 0

Вектор будет перпендикулярен вектору в пределе_, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением

Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.

Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при

Длина дуги АВ это путь, пройденный точкой от А до В,

Умножим наи получим:

В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:

Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными

А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.

Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.

— движение криволинейное, так как траекторией является окружность;

— движение равномерное, так как модуль скорости не меняется;

— вектор скорости направлен по касательной к окружности;

-вектор ускорения направлен к центру окружности;

— модуль центростремительного ускорения равен:

Примеры и разбор решения заданий

1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?

При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением

где R = 50 м; υ= км/ч = 10 м/с.

2. Две материальные точки движутся по окружностям радиусами R₁ = 10 см и R₂ = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?

Задано два объекта:

1) материальная точка, которая движется по окружности R₁;

2) материальная точка, которая движется по окружности R₂.

При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением

Для тела 1 уравнение (1) примет вид:

Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.

Источник