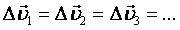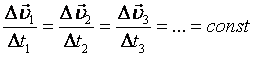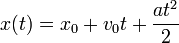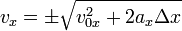Что такое равнопеременное движение физика 9 класс

Равнопеременное движение. Ускорение.

Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.

Пусть Δt₁= Δt₂=Δt₃=. тогда по определению

Следовательно,

Т.о., это характеристика движения.

Если t₀=0, то

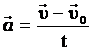
В случае не равнопеременного движения:

тогда мгновенное ускорение

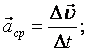
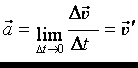
Графики равнопеременного движения.

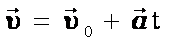
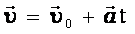
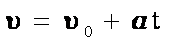
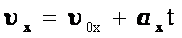
или – через модули.

Движения, совпадающие с направлением координатной оси:

Источник

Равнопеременное движение

В общем случае равноускоренным движением называется движение, при котором вектор ускорения 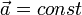. Напомним, что это означает постоянство как по модулю, так и по направлению.

Примером такого движения является движение тела, брошенного под углом α к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением 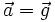, направленным вертикально вниз.

При равноускоренном движении скорость тела определяется формулой:

Примечание. Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора 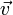и противонаправлены). Равнозамедленное движение также является равноускоренным.

Перемещение в случае одномерного равноускоренного движения

В случае одномерного равноускоренного движения вдоль координаты x имеет место формула:

,

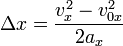
Криволинейное равноускоренное движение также можно рассматривать как одномерное. В этом случае используется обобщённая координата S, часто называемая путём. Эта координата соответствует длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

,

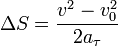
где a_τ — тангенциальное ускорение, которое «отвечает» за изменение модуля скорости тела.

Из вышеприведенных формул можно получить выражения для определения конечной скорости тела, при известных начальной скорости, ускорении и перемещении:

В случае криволинейного равноускоренного движения имеем:

Аналогичные соотношения можно записать для выражений:

; .

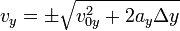
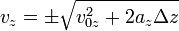
И найти конечную скорость по теореме Пифагора

.

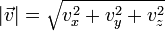
Теорема о кинетической энергии

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

.

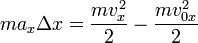
Записав аналогичные соотношения для координат y и z и просуммировав все три равенства получим соотношение:

.

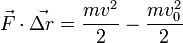
Слева стоит работа постоянной равнодействующей силы 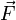, а справа — разность кинетических энергий в конечный и начальный момент движения.

Полезное

Смотреть что такое «Равнопеременное движение» в других словарях:

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ — движение точки, при к ром её касательное ускорение wt (в случае прямолинейного Р. д. всё ускорение w) постоянно. Скорость v, к рую имеет точка через время t после начала движения, и её расстояние s от нач. положения, измеренное вдоль дуги… … Физическая энциклопедия

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ — движение точки, при котором ее касательное ускорение (в случае прямолинейного равнопеременного движения все ускорение) постоянно … Большой Энциклопедический словарь

равнопеременное движение — движение точки, при котором её касательное ускорение (в случае прямолинейного движения полное ускорение) постоянно. * * * РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ, движение точки, при котором ее касательное ускорение (в случае… … Энциклопедический словарь

Равнопеременное движение — движение точки, при котором её касательное ускорение wτ (в случае прямолинейного Р. д. всё ускорение w) постоянно. Скорость v, которую имеет точка через t сек после начала движения, и её расстояние s от начального положения, измеренное… … Большая советская энциклопедия

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ — движение точки или тела, при к ром тангенциальное ускорение ат постоянно. При Р. д. за равные промежутки времени Дедьта t значение скорости точки (тела) изменяется на одну и ту же величину Дедьта v = ат Дедьта t … Большой энциклопедический политехнический словарь

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ — движение точки, при к ром её касательное ускорение (в случае прямолинейного движения полное ускорение) постоянно … Естествознание. Энциклопедический словарь

Равноускоренное движение — в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения Равноускоренное движение движение, при котором ненулевой вектор ускорения ос … Википедия

Кинематика (физика) — У этого термина существуют и другие значения, см. Кинематика. Кинематика (греч. κινειν двигаться) в физике раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения… … Википедия

Источник

Презентация по физике для 9 класса на тему «Равномерное и равнопеременное движение»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Механика
Равномерное и равнопеременное движение

Описание слайда:

Основные характеристики механического движения
Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.

Описание слайда:

Механическое прямолинейное движение
равномерное
неравномерное
равноускоренное
С переменным ускорением
равнозамедленное

Описание слайда:

Описание слайда:

Описание слайда:

t – время, [t] = с (секунда)

Описание слайда:

Описание слайда:

Уравнения равномерного движения

Описание слайда:

Графики равномерного движения
x

t
t
График координаты
График скорости

Описание слайда:

3. Равнопеременное движение
это движение, при котором скорость за любые равные промежутки времени изменяется одинаково.

Описание слайда:

Равнопеременное движение
Примеры:
Торможение или разгон автомобиля
Движение по наклонной плоскости
Свободное падение

Описание слайда:

Описание слайда:

Описание слайда:

Уравнения равнопеременного движения

Описание слайда:

Описание слайда:

Описание слайда:

Описание слайда:

Запишите уравнение скорости от времени для каждого участка графика
Vx м/с
t,с
0
60
-60
3
5
6
7
А
В
С
D
F
ОТВЕТ:
ОА: V=20t
АB: V=60
BD: V=60-60t
DF: V=-60

Описание слайда:

Описание слайда:

Описание слайда:

Описание слайда:

Задача 3: При подходе к станции поезд начал торможение, имея начальную скорость 90 км/ч и ускорение 0,1 м/с2. Определите тормозной путь поезда, если торможение длилось 1 мин.

Описание слайда:

Задача 4: Вагон движется равнозамедленно с ускорением 0,5 м/с2. Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Описание слайда:

Задача 5: Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Описание слайда:

Задача 6: Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равнозамедленно с ускорением 0,6 м/с2. Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Описание слайда:

Задача 7: (ОГЭ) Поезд, идущий со скоростью v0 = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Физика: теория и методика преподавания в образовательной организации

Курс профессиональной переподготовки

Методическая работа в онлайн-образовании

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Презентация по физике для 9 класса на тему «Радиоактивные превращения. Ядерные реакции»

Презентация по физике для 10 класса на тему «Электростатика»

Контрольная работа по физике для 9 класса на тему «Вселенная»

Примеры решения комбинированных задач по физике

Конспект урока физики в 10 классе. Тема. Электрический ток в вакууме. Электронно-лучевая трубка.

Конспект урока физики в 10 классе. Тема: Закон Кулона.

КВН по физике для учащихся 11 класс.

Статья на тему: Обобщение опыта работы учителя физики Дзауровой Аминат Висангиреевны»»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5373312 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

В МГПУ сформулировали новые принципы повышения квалификации

Время чтения: 4 минуты

Утверждены сроки заключительного этапа ВОШ

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

МГУ откроет первую в России магистерскую программу по биоэтике

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Равнопеременное движение

Рассмотрим прямолинейное движение тела вдоль оси (одномерный случай) и пусть при этом скорость тела изменяется.

Когда скорость изменяется, появляется ускорение. Ускорение, в свою очередь, тоже может меняться.

Если изменяется и ускорение, и скорость тела – движение сложное, например, колебательное;

Движение равнопеременное — если изменяется только скорость, а ускорение постоянное.

Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину.

При этом, если скорость увеличивается – движение называют равноускоренным, а если скорость уменьшается – равнозамедленным.

Примечание: Вместо слов «ускорение постоянное» можно произнести «ускорение не меняется», или «ускорение одно и то же».

Рекомендую предварительно ознакомиться с основными терминами для описания движения.

Будем выбирать направления для векторов скорости и ускорения относительно оси. Разберем несколько возможных вариантов.

Равноускоренное движение

Пусть при движении по прямой скорость тела увеличивается. Обратим внимание на перемещение тела.

Примечание: Движение равноускоренное, значит, за одинаковые интервалы времени перемещение будет увеличиваться на одну и ту же величину.

Этот факт иллюстрирует рисунок 1. Из рисунка видно: по сравнению с первой секундой, за вторую секунду пути перемещение увеличивается на небольшой отрезок, а за третью секунду – на два таких отрезка.

Считаем, что векторы скорости и ускорения сонаправлены с осью, вдоль которой движется тело (рис. 2).

Примечание: Скорость увеличивается, когда вектор ускорения сонаправлен с вектором скорости.

В начальный и в конечный моменты времени скорости будут различаться.

Формулы можно записать в скалярном виде, так как движение происходит вдоль одной прямой и направления векторов известны.

Связь между начальной и конечной скоростью выглядит так:

Уравнение движения выглядит так:

\[ S = v_ <0>\cdot t + a \cdot \frac <2>\]

\[ x – x_ <0>= v_ <0>\cdot t + a \cdot \frac <2>\]

Кроме уравнения движения теперь есть связь между скоростями. Поэтому, решая задачи, в которых скорость увеличивается, используем систему, состоящую из двух таких уравнений:

\[ \large \boxed < \beginv = v_ <0>+ a \cdot t \\ S = v_ <0>\cdot t + a \cdot \frac <2>\end > \]

Примечание: Перемещение тела можно вычислить, не обладая информацией о времени движения, зная только начальную и конечную скорость тела и его ускорение. Об этом подробно написано в статье о формуле пути без времени.

Равнозамедленное движение

Пусть теперь тело движется по прямой и его скорость уменьшается. Рассмотрим перемещение тела.

Примечание: Движение равнозамедленное, значит, за одинаковые интервалы времени перемещение будет уменьшаться. При чем, на одну и ту же величину.

На рисунке 3 представлено изменение перемещения. Видно, что по сравнению с первой секундой, за вторую секунду перемещение уменьшается на небольшой отрезок, а за третью секунду – на два таких отрезка.

Примечание: Скорость будет уменьшаться, когда вектор ускорения направлен противоположно вектору скорости.

Пусть вектор скорости сонаправлен с осью, вдоль которой движется тело, а вектор ускорения – направлен против этой оси.

В начале и в конце пути скорости будут различаться.

Формулы можно записывать в скалярном виде, так как движение происходит вдоль одной прямой. Будем использовать знаки проекций векторов на ось.

Связь между скоростями выглядит так:

А уравнение движения имеет такой вид:

\[ S = v_ <0>\cdot t — a \cdot \frac <2>\]

Заменив перемещение разностью конечной и начальной координат \( S = x — x_<0>\), получим:

\[ x – x_ <0>= v_ <0>\cdot t — a \cdot \frac <2>\]

Значит, когда скорость уменьшается, для решения задач нужно использовать систему из двух таких уравнений:

\[ \large \boxed < \beginv = v_ <0>— a \cdot t \\ S = v_ <0>\cdot t — a \cdot \frac <2>\end > \]

Расшифруем теперь, к примеру, словосочетание «прямолинейное равнозамедленное движение» — это движение по прямой, ускорение есть, оно не меняется. Скорость тела уменьшается, так как вектор ускорения направлен противоположно вектору скорости.

Примечание: Перемещение замедляющегося тела можно вычислить не используя время. Потому, что существует запись формулы пути без времени для случая, когда скорость тела уменьшается.

Скорость направлена против оси, а ускорение – по оси

Дополнительно рассмотрим случай, когда скорость и ускорение направлены в противоположные стороны, ускорение – по оси, а скорость – против оси (рис. 5).

А если тело продолжит движение, то начнет двигаться в обратную сторону и модуль его скорости начнет увеличиваться. Поэтому, такое движение будет равноускоренным и будет сонаправленным с вектором ускорения.

Когда скорость направлена против оси, ее проекция на ось отрицательна и в уравнение она войдет со знаком минус. Ускорение же, напротив, совпадает с направлением оси, поэтому, войдет в уравнение со знаком «+».

Запишем связь между скоростями:

Уравнение движения для рассмотренного случая имеет такой вид:

\[ x – x_ <0>= — v_ <0>\cdot t + a \cdot \frac <2>\]

Для выбранного направления векторов в итоге получим такую систему уравнений:

\[ \large \boxed < \beginv = — v_ <0>+ a \cdot t \\ x – x_ <0>= — v_ <0>\cdot t + a \cdot \frac <2>\end > \]

Решая задачи на движение, иногда вычисляют мгновенную и среднюю скорости.

Термины «мгновенная скорость» и «средняя скорость» применяют для случаев, когда скорость изменяется – то есть, для неравномерного движения.

Мгновенная скорость

Мгновенная скорость – это скорость тела в какое-то мгновение. Когда скорость тела меняется, то в различные мгновения (моменты времени) скорости будут различаться.

Мгновенную скорость v вычисляют, вместо символа t подставляя в формулу интересующее нас время:

Знак ускорения зависит его направления.

Средняя скорость

Средняя скорость тела – скорость, с которой нужно двигаться равномерно, чтобы пройти тот же путь за то же время.

Другими словами, средняя скорость помогает понять, с какой постоянной скоростью могло бы двигаться тело, чтобы пройти весь пройденный путь за такое же время.

Примечания:

Формула для расчета средней скорости:

\( S_<\text<весь>>(\text<м>) \) ​– полный путь, пройденный телом;

\( t_<\text<полное>> \left( c \right)\) – время, за которое тело прошло весь путь.

Источник

Прямолинейное равнопеременное движение

Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.

Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:

Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.

Рис. 1. Равноускоренное движение 1

Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:

Рис. 2. Равноускоренное движение-2

Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( ) направлен против оси OX (рис. 2). Проецируем:

Рис. 3. Равноускоренное движение-3

Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:

Рис. 4. Равноускоренное движение-4

Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:

Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.

Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:

Подставим (3) в (2) при условии :

Таким образом, мы получили формулу, в которой нет параметра времени.

Источник