Что такое равносильные логические выражения

Равносильные логические выражения.

Логические выражения, у которых таблицы истинности совпадают, называются равносильными.

Для обозначения равносильных логических выражений используется знак равенства «=».

Докажем с помощью таблиц истинности (таблицы 5 и 6), что выражения & и АvВ равносильны.

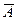
А

В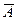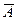

&

А

В

АvB

АvВ

Таблицы истинности совпадают, следовательно логические выражения равносильны:

& и АvВ

АППАРАТНОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Принципы фон Неймана и классификация ЭВМ.

В 1946 г. Джон П. Экерт (род. 1919) и Джон В. Могли (1907—1980) разработали один из первых компьютеров для армии США— ENIAC (электронный числовой интегратор и калькулятор) на электронных лампах.

В 1945 г. к работе Могли и Экерта был привлечен знаменитый математик Джон фон Нейман, который подготовил доклад об этой машине. Доклад был разослан многим ученым и получил широкую известность, поскольку в нем фон Нейман ясно и просто сформулировал общие принципы функционирования универсальных вычислительных устройств, т.е. компьютеров.

Дата добавления: 2015-11-12 ; просмотров: 1037 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Равносильные логические выражения

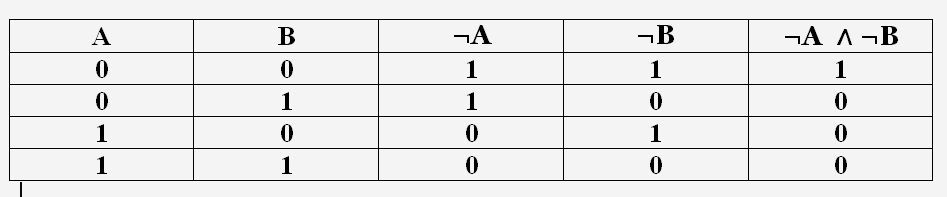
Логические выра­жения, у которых последние столбцы таблиц истинности сов­падают, называются равносильными. Для обозначения равно­сильных логических выражений используется знак «=». Докажем, что логические выражения ¬А ∧ ¬В и ¬(A ∨ B) равно­сильны. Построим сначала таблицу истинности логического выражения ¬А ∧ ¬В.

Теперь построим таблицу истинности логического выражения ¬(A ∨ B).

Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:

В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие: «если. то. », «. тогда и только тогда, когда. » и др. Не­которые из них имеют свое название и свой символ, и им со­ответствуют определенные логические функции.

Логическое следование (импликация)

Логическое следо­вание (импликация) образуется соединением двух высказы­ваний в одно с помощью оборота речи «если. то. ».

Логическая операция импликации «если А, то В», обо­значается А → В.
Составное высказывание, образованное с помо­щью операции логического следования (импли­кации), ложно тогда и только тогда, когда из ис­тинной предпосылки (первого высказывания) сле­дует ложный вывод (второе высказывание).

Однако операция логического следования несколько от­личается от обычного понимания слова «следует». Если пер­вое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (выво­да) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следо­вать что угодно.

В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базо­вым: логическому умножению, логическому сложению и ло­гическому отрицанию.

Таблица истинности логического выражения ¬A ∨ B

Таблицы истинности совпадают (т.е. значения в последних столбцах одинаковы), следовательно А → В = ¬A ∨ B.

Л огическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А

Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Таблица истинности логической функции эквивалентности

Рассмотрим, например, два высказывания: А=»Компьютер может производить вычисления» и В=»Компьютер включен». Составное высказываение, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны:

«Компьютер может проводить вычисления тогда и только тогда, когда компьютер включен».

«Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».

Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание истинно, а другое ложно:

«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».

«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».

Докажем, используя таблицы истинности, что операция эквивалентности А

Таблицы истинности совпадают (т.е. значения в последних столбцах одинаковы), следовательно А

Предыдущий урок Следующий урок

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Логические выражения.

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§11. Логические выражения.

Формализация

Ключевые слова:

Обозначив простые высказывания буквами — логическими переменными и используя логические операции, можно записать любое высказывание в виде логического выражения.

Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).

Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолёта. Обозначим высказывания:

А = Первый двигатель вышел из строя;

В = Второй двигатель вышел из строя;

С = Третий двигатель вышел из строя;

X = Аварийная ситуация.

Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):

X = (А и В) или (А и С) или (В и С).

Это выражение может быть записано с помощью других обозначений:

X = (А • В) + (А • С) + (В • С). (*)

Таким образом, мы выполнили формализацию.

Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.

При вычислении логических выражений установлен такой порядок выполнения операций:

1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.

Можно ли убрать скобки в выражении (*)? Почему?

Уберите лишние скобки в логических выражениях:

а) X = (А + (В • С) • (А + С));

б) X = (А + B) • (C • А) • (А + (B + C))).

Вычислите значение логического выражения X = (А • В + С) • (А + C) при:

а) А = О, В = О, С = 1;
б) А = О, В = 1, С = 1;
в) А = 1, В = 1, С = 0.

Таблицы истинности

Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения

X = А и не В или не А и B,

которое можно также записать в виде

Сколько строк в таблице истинности выражения с двумя переменными?

Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).

Рис. 2.18

Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.

Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.

Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.

Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.

Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?

Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.

Сколько строк в таблице истинности выражения с тремя переменными?

Постройте таблицу истинности логического выражения

Х = А • В + А • С + В • С.

Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).

Рис. 2.19

Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?

Всего в таблице истинности функции от трёх переменных 2 3 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.

Сколько различных значений можно закодировать с помощью 5 бит?

Как вы нашли это значение?

Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:

Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.

Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.

Проверьте самостоятельно, подходят ли остальные варианты.

Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:

Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).

Рис. 2.20

Выясним, какие из следующих функций могут соответствовать этой таблице:

Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:

Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.

Кратко решение можно записать так:

1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;

2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;

3) этим условиям удовлетворяют функции в) и д).

Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).

Рис. 2.21

Выясните, какие из следующих функций могут соответствовать этой таблице:

Составление условий

Логические выражения часто используются при решении математических задач с помощью компьютеров.

Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).

Рис. 2.22

На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:

Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:

(1 ≤ х) и (х ≤ 3) или (5 ≤ х) и (х ≤ 8).

Запишите условие, которое определяет область на рис. 2.22, в.

Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).

Рис. 2.23

Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.

Рис. 2.24

Запишите условие, которое определяет области на рисунках (рис. 2.25).

Рис. 2.25

Построим логическое выражение для области на рис. 2.26.

Рис. 2.26

Можно разделить заштрихованную область на две части (рис. 2.27).

Рис. 2.27Обе области находятся внутри круга радиуса 1 с центром в начале координат, т. е. в области х 2 + у 2 ≤ 1. Первая область описывается выражением

(х 2 + у 2 ≤ 1) и (х ≤ 0),

а вторая — выражением

Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):

Общее условие х 2 + у 2 ≤ 1 можно вынести за скобки:

Попробуйте ещё упростить полученное условие.

Запишите условие, которое определяет области на рисунках (рис. 2.28).

Рис. 2.28

Логические схемы

Вернёмся снова к примеру с системой аварийной сигнализации самолёта. Предположим, что на каждом двигателе установлен логический датчик, который выдаёт условный сигнал 1 (например, высокий уровень напряжения), если двигатель неисправен, и условный сигнал 0, если двигатель исправен. Требуется построить логическую схему — схему логического устройства, — которая при аварии выдаёт условный сигнал 1, а в режиме нормальной работы — сигнал 0.

Сигналы от трёх двигателей назовём А, Б и С. В начале параграфа мы уже составили логическое выражение для запуска аварийной сигнализации:

Х = А • В + А • С + В • С.

Здесь три логических умножения и два логических сложения. Сначала выполняются все операции умножения (слева направо), а затем — все операции сложения (тоже слева направо). Расставим номера операций:

Последней выполняется вторая операция сложения. Поэтому последний элемент в схеме — это элемент логического сложения ИЛИ (рис. 2.29).

Рис. 2.29

На первый вход этого элемента ИЛИ подаётся сигнал А • В + А • С, в этом выражении последняя операция — логическое сложение, добавляем ещё один элемент ИЛИ (рис. 2.30).

Рис. 2.30

Три операции логического умножения добавляют в схему три элемента И (рис. 2.31).

Рис. 2.31

Запишите в тетради логическое выражение по логической схеме (рис. 2.32).

Рис. 2.32

Постройте логическую схему, соответствующую выражению:

в) Z = A • B + A • B • C.

Работа в парах. Один из вас пусть нарисует логическую схему для выражения X = A + В • С (черта сверху обозначает, что операция отрицания применяется ко всему выражению), а второй — для выражения Y = (А + В) (А + С). Постройте таблицы истинности для своих выражений и сравните их. Какую формулу вы сейчас вместе доказали?

Работа в парах. Запишите логическое выражение, включающее 5-6 операций, и предложите соседу нарисовать логическую схему. Проверьте и обсудите с ним его решение.

Путешествуя по Зазеркалью, Алиса увидела дверь с тремя кнопками, которые были отмечены буквами А, В и С. На двери висела схема (рис. 2.33).

Рис. 2.33

На какую (одну!) из трёх кнопок нужно нажать Алисе, чтобы открыть дверь?

Выводы

• Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.

• В логических выражениях операции выполняются в следующем порядке:

1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.

Для изменения порядка действий используются скобки.

• Таблица истинности логического выражения показывает, чему равно значение выражения при всех возможных комбинациях значений исходных переменных.

• Логические выражения, истинность которых зависит от значений исходных переменных, называют вычислимыми.

• Логическое выражение, которое всегда истинно, называется тождественно истинным или тавтологией. Выражение, которое всегда ложно, называют тождественно ложным или противоречием. Пример тождественно истинного выражения: А + А, пример тождественно ложного: А • А.

• Два выражения, принимающие одинаковые значения при всех значениях переменных, называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Что можно сделать для того, чтобы изменить порядок выполнения действий в логических выражениях?

2. Поясните разницу между терминами «логическое выражение» и «логическая функция».

3. Как можно доказать (или опровергнуть) логическую формулу?

4. Можно ли сказать, что таблица истинности однозначно определяет:

а) логическое выражение;
б) логическую функцию?

5. Что такое вычислимое логическое выражение?

6. Что такое равносильные выражения?

7. Выполните по указанию учителя задания в рабочей тетради.

Источник