Что такое равновеликие параллелограммы

Равновеликие фигуры

Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.

Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).

Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.

1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.

То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если

2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.

Площадь квадрата S=3²=9.

Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если

3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.

Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если

Источник

Математика

На чер. 73 дано построение равновеликих параллелограммов, имеющееся у Евклида. Этим построением можно пользоваться для решения различных задач на превращение параллелограмма или прямоугольника в равновеликий ему, удовлетворяющий известным требованиям.

Например, легко решается, без сведения дела к измерению, задача: построить прямоугольник, равновеликий данному и имеющий данное основание (обычно, опираясь на знание того, что площадь прямоугольника равна произведению основания на высоту, задачу сводят к построению 4-го пропорционального отрезка).

Решение этой задачи, без сведения к алгебре, таково: пусть ABCD (чер. 102) – данный прямоугольник; отложив отрезок AE, равный данному основанию искомого прямоугольника, и состроив EL || AD, а заем прямую AF, где F точка пересечения EL с DC, и построив MK || BA (точка M есть точка пересечения BC и AF), получим прямоугольник ABMK, для которого видим, что прямоугольник AELK имеет данное основание AE и равновелик данному прямоугольнику ABCD.

Это решение задачи было давно известно, хотя и не пользуется распространением. Под его влиянием может возникнуть мысль изыскать решение, построенное на той же идее, другой общеизвестной задачи: построить квадрат, равновеликий данному прямоугольнику.

Предварительно надо ознакомиться с так называемой «прямой Симсона».

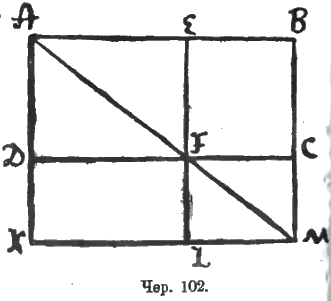
Если в круг вписан треугольник ABC (чер. 103) и если из какой-либо точки M окружности построены перпендикуляры MD, ME и MF на его стороны, то, как известно, основания этих перпендикуляров, точки D, E и F, лежат на одной прямой, называемой «прямая Симсона».

Вот выяснение этого.

Угол ADM – прямой; следов., точка D лежит на окружности, диаметром которой служит отрезок AM. Так как ∠AEM тоже прямой, то точка E лежит на той же окружности. Поэтому углы AMD и AED суть углы, вписанные в эту окружность и опирающиеся на одну и ту же дугу AD (она на чертеже не дана). Следов., ∠AED = AMD.

Так как ∠MEC = d и ∠MFC = d, то точка E и F лежат на окружности, диаметром которой служит отрезок MC, и углы CMF и CEF суть вписанные в эту окружность и опирающиеся на одну и ту же дугу CF (не нарисованную на чертеже). След., ∠CEF = ∠CMF.

Так как четырехугольник MABC вписан в круг, то ∠AMC + ∠B = 2d.

Так как углы при точках D и F в четырехугольнике MDBF прямые, то этот четыреугольник есть вписываемый и, следов., ∠DMF + ∠B = 2d.

Отсюда мы выводим, что ∠AMC = ∠DMF. Так как ∠AMC = ∠AMD + ∠DMC и ∠DMF = ∠DMC + ∠CMF, то отсюда имеем:

∠AMD + ∠DMC = ∠DMC + ∠CMF
или
∠AMD = ∠CMF.

Но мы получили, что ∠AED = ∠AMD и ∠CEF = ∠CMF. Следов., ∠AED = ∠CEF.

Так как AEC есть прямая линия, то равенство углов AED и CEF указывает на то, что DEF есть также прямая линия.

Известна и обратная теорема: если из какой-либо точки плоскости треугольника опущены перпендикуляры на его стороны и если их основания расположены на одной прямой, то указанная точка расположена на окружности, описанной около треугольника.

Выяснение этого немного отличается от предыдущего. Мы теперь не знаем, что четыреугольник ABCM есть вписываемый, но зато знаем, что DEF есть прямая и, следовательно, ∠AED = ∠CEF. Так как по-прежнему точки A и E лежат на окружности, диаметром которой служит отрезок DM, и точки E и F лежат на окружности, диаметром которой служит отрезок MC, то по-прежнему имеем: ∠AED = ∠AMD и ∠CEF = ∠CMF.

Отсюда заключаем, что ∠AMD = ∠CMF. Так как четыреугольник MDBF по-прежнему вписываемый (ибо углы при D и F прямые), то ∠DMF + ∠B = 2d или ∠DMC + ∠CMF + ∠B = 2d или ∠DMC + ∠AMD + ∠B = 2d или ∠AMC + ∠B = 2d, откуда и заключаем, что точка M лежит на круге, описанном около ∆ABC.

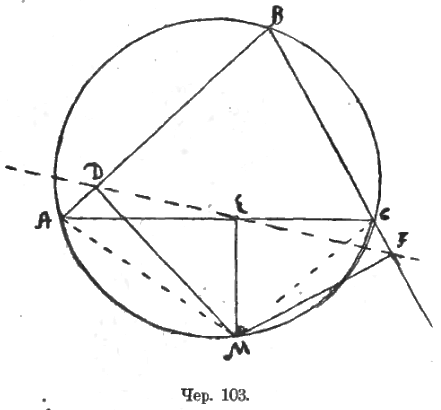
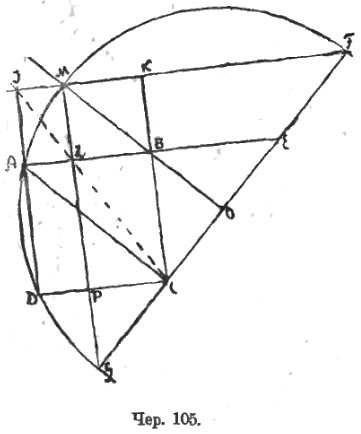
Пусть ABCD (чер. 104) есть данный прямоугольник и ALJK – искомый квадрат. Тогда вершина J этого квадрата должна лежать на биссекторе AJ прямого угла A данного прямоугольника. Далее искомая точка J должна занять на этом биссекторе такое положение чтобы точка A, G и Н лежали на одной прямой. Точки G и H суть основания перпендикуляров, опущенных из точки J на прямые DC и BC. Тогда возникает мысль применить сюда «прямую Симсона». Примем прямые DC и BC за 2 стороны треугольника, третьею же его стороною должна быть прямая, перпендикулярная к AJ. Эта прямая MN легко строится. Получим ∆MCN. Центр O этой окружности (ибо ∠MCN прямой) должен лежать в середине отрезка MN. Раз точка J определена, то построение квадрата KJLA не вызывает затруднений.

Та же идея может быть применена к задаче деления отрезка в крайнем и среднем отношении. Если дан отрезок AB, то задача сводится к разделению этого отрезка на такие две части AL и LB, чтобы квадрат, построенный на большей из них, на отрезке LB, был равновелик прямоугольнику, сторонами которого служат сам отрезок AB и другая часть его, именно AL.

Точка A должна лежать, согласно обратной теореме о «прямой Симсона», на окружности, описанной около ∆GMF, а центр O этой окружности должен лежать на середине отрезка CE, откуда вытекает построение для определения точки M: 1) строим на AB квадрат ABCD и его диаг. AC, 2) строим через точку C прямую GF ⊥ AC, – тогда определится точка E, 3) делим отрезок CE пополам в точке O, 4) строим прямую через O и B, – эта прямая образует со сторонами BC и AB углы в 45° (ибо ∆CBE равнобедренный), 5) строим окружность, принимая точку O за центр и OA (или OD) за радиус, – пересечение этой окружности с прямою OB определит точку M. Раз точка M определена, то построив MLP ⊥ AB, соединив M с F и продолжив CB до пересечения в точке K с MF, получим квадрат LMKB (так как диагональ BM составляет со сторонами BL и BK углы по 45°), равновеликий прямоугольнику ALPD, что и дает решение задачи.

Источник

Параллелограмм: свойства и признаки

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Как найти площадь параллелограмма:

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Площадь. Равновеликие фигуры

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.

Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

Перекраивание трапеции в равносоставленный треугольник:

Пло­щадь тра­пе­ции с ос­но­ва­ни­я­ми длин a и b и дли­ной вы­со­ты h рав­на S=(a+b)/2•h. Убе­дить­ся в этом мож­но вос­поль­зо­вав­шись фор­му­лой для вы­чис­ле­ния пло­ща­ди тре­уголь­ни­ка. Для это­го необ­хо­ди­мо разре­зать тра­пе­цию на та­кие ча­сти, из ко­то­рых мож­но со­ста­вить треугольник.

Разре­жем тра­пе­цию вдоль ли­нии, со­еди­ня­ю­щей вер­ши­ну с се­ре­ди­ной проти­во­по­лож­ной бо­ко­вой сто­ро­ны. По­вер­нём от­ре­зан­ный тре­уголь­ник до того момен­та, ко­гда оба ос­но­ва­ния тра­пе­ции ока­жут­ся на од­ной прямой. Убедитесь, что две ча­сти бо­ко­вой сто­ро­ны при этом ля­гут на од­ну прямую, то есть, получится дей­стви­тель­но тре­уголь­ник.

Одна из сторон получив­ше­го­ся тре­уголь­ни­ка име­ет дли­ну, рав­ную сум­ме длин оснований трапе­ции, а дли­на вы­со­ты тре­уголь­ни­ка, про­ве­дён­ной к этой стороне, сов­пада­ет с вы­со­той тра­пе­ции.

Один из способов подсчё­та пло­ща­ди тре­уголь­ни­ка со­сто­ит в на­хож­де­нии половины произве­дения дли­ны сто­ро­ны на дли­ну вы­со­ты, опу­щен­ную на эту сторону. При­ме­нение это­го спо­со­ба и да­ёт при­выч­ную фор­му­лу площа­ди трапеции.

Модель мож­но сде­лать из доски толщиной около 10 мм. Для удобства демон­стра­ции две ча­сти, на которые она разрезает­ся, удобно со­еди­нять между собой при по­мо­щи маг­ни­тов.

Равносоставленность

Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.

Источник

Равновеликие фигуры

Презентация к уроку

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы:

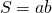
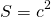
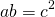
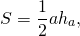
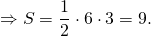
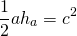
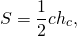
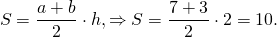
Источник