Что такое равные фигуры в геометрии 7 класс

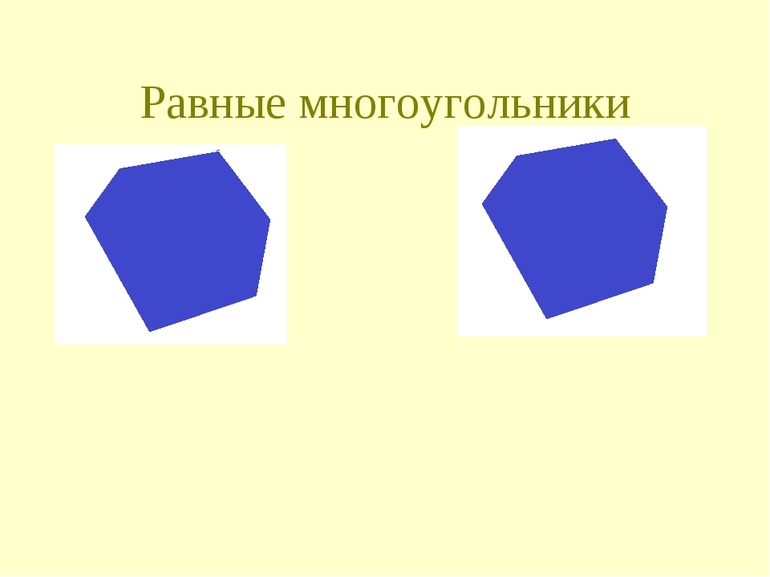
Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

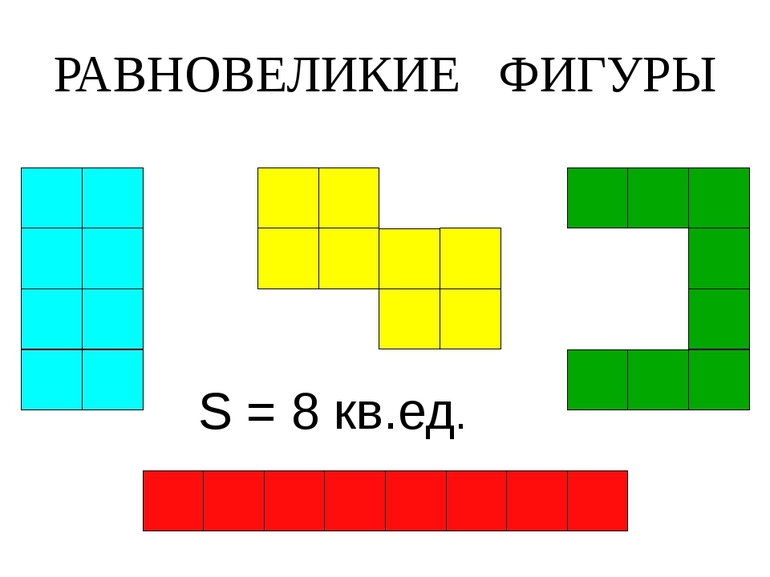
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Визуальный способ

Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.

Источник

Словарь геометрических понятий 7-8 класс

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Геометрия,7-9 Основные определения, теоремы, формулы

7 класс Глава I Начальные геометрические сведения

Первичные понятия: точка, прямая, плоскость, пространство, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов

Отрезок-часть прямой, ограниченная двумя точками.

Луч-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны.

Угол-часть плоскости, ограниченная двумя лучами, выходящими из одной точки.

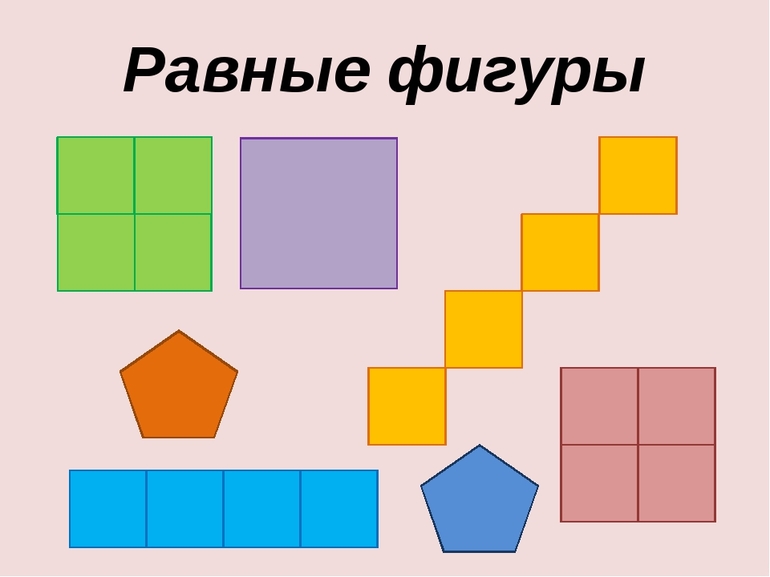
Равные фигуры-фигуры, которые совпадают при наложении друг на друга.

Середина отрезка-точка на отрезке, делящая его пополам.

Биссектриса угла-луч, выходящий из вершины угла и делящий его пополам.

Единицы измерения длины отрезка: миллиметры, сантиметры, дециметры, метры, километры.

Единицы измерения углов: градус, минуты, секунды.

Длина отрезка-количество единиц измерения длины, вмещающихся между двумя концами отрезка.

Градусная мера угла-количество единиц измерения углов, вмещающихся между сторонами угла.

Смежные углы – это два угла, у которых одна сторона общая,а две других образуют прямую линию.

Вертикальные углы-два угла, у которых стороны одного угла являются продолжением сторон другого.

Свойство: вертикальные углы равны.

Перпендикулярные прямые-прямые, которые при пересечении образуют прямой угол.

Параллельные прямые-прямые, лежащие в одной плоскости и не имеющие общих точек.

Глава II Треугольники

Треугольник-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника.

Периметр – сумма длин всех сторон.

Теорема(первый признак равенства треугольников): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Теорема: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Медиана треугольника— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Равнобедренный треугольник-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.

Равносторонний треугольник— треугольник, у которого все стороны равны.

Свойство:в равнобедренном треугольнике углы при основании равны.

Свойство:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Теорема(второй признак равенства треугольников): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Теорема(третий признак равенства треугольников): если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Окружность-геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки-центра.

Радиус окружности-отрезок,соединяющий любую точку окружности с её центром.

Хорда-отрезок, соединяющий две любые точки окружности.

Диаметр-хорда, проходящая через центр.

Дуга – часть окружности, ограниченная двумя точками.

Основные задачи на построение циркулем и линейкой:

построение отрезка, равного данному

построение угла, равного данному

построение биссектрисы угла

построение середины отрезка

построение перпендикулярных прямых

Глава III Параллельные прямые

При пересечении двух прямых третьей прямо-секущей образуются следующие виды углов:

накрест лежащие углы

Теорема(первый признак параллельности прямых):если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема(второй признак параллельности прямых):если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Аксиома: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Теорема:если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Теорема:если две прямые параллельны третьей прямой, то они параллельны.

Теорема:если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Теорема:если две параллельные прямые пересечены секущей, то соответственные углы равны.

Глава IV Соотношения между сторонами и углами треугольника

Внешний угол треугольника-угол, смежный с каким-либо внутренним углом треугольника.

Остроугольный треугольник-это треугольник, все внутренние углы которого острые.

Тупоугольный треугольник-это треугольник, у которого один из углов тупой.

Прямоугольный треугольник-это треугольник, у которого один из углов прямой.

Гипотенуза-это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Катеты-это стороны прямоугольного треугольника, образующие прямой угол.

Теорема:в треугольнике против большей стороны лежит больший угол.

Теорема:в треугольнике против большего угла лежит большая сторона.

Следствие:в прямоугольном треугольнике гипотенуза всегда больше катета.

Теорема(признак равнобедренного треугольника):если в треугольнике два угла равны, то он равнобедренный.

Теорема(неравенство треугольника):каждая сторона треугольника меньше суммы двух других сторон.

Теорема(признак равенства прямоугольных треугольников):если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Теорема(признак равенства прямоугольных треугольников):если катет и прилежащий к нему острый угол одного прямоугольного треугольника равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Теорема(признак равенства прямоугольных треугольников):если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Теорема(признак равенства прямоугольных треугольников):если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на прямую.

Теорема:все точки каждой из двух параллельных прямых равноудалены от другой прямой.

8 класс. Глава V Четырёхугольники

Многоугольник-фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.

Диагональ-это отрезок, соединяющий две несоседних вершины многоугольника.

Выпуклый многоугольник— это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны.

Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.

Свойство:диагонали параллелограмма точкой пересечения делятся пополам.

Теорема(признак параллелограмма):Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Теорема(признак параллелограмма):Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.

Теорема(признак параллелограмма):Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Трапеция-это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.

Равнобедренная трапеция-это трапеция, у которой боковые стороны равны.

Прямоугольная трапеция-это трапеция, у которой один из углов прямой.

Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Прямоугольник-это параллелограмм, у которого все углы прямые.

Свойство: диагонали прямоугольника равны.

Теорема(признак прямоугольника):если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Ромб-это параллелограмм, у которого все стороны равны.

Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Квадрат-это прямоугольник, у которого все стороны равны.

Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его смежных сторон.

Площадь параллелограмма равна произведению его основания на высоту.

Площадь треугольника равна половине произведения его основания на высоту.

Площадь прямоугольного треугольника равна произведению его катетов.

Если высоты двух треугольников равны, то их площади относятся как основания.

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Площадь трапеции равна полусумме её оснований на высоту.

Теорема Пифагора:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема(обр.):если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.

Глава VII Подобные треугольники

Отрезки m и n пропорциональны отрезкам m ₁и n ₁,если отношения их длин равны m : m ₁= n : n _1.

Подобные треугольники— это треугольники, у которых соответственные углы равны, а сходственные стороны пропорциональны.

Коэффициент подобия- это число, равное отношению сходственных сторон подобных треугольников.

Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Теорема(первый признак подобия треугольников):если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Теорема(второй признак подобия треугольников):если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Теорема(первый признак подобия треугольников):если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.

С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.

Синус острого угла прямоугольного треугольника- это отношение противолежащего катета к гипотенузе.

Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.

Глава VIII Окружность

Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.

Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

Центральный угол – это угол с вершиной в центре окружности.

Дуга окружности измеряется центральным углом, который на неё опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Т.Вписанный угол равен половине дуги, на которую он опирается.

С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.

Средняя линия трапеции— это отрезок, соединяющий середины её боковых сторон.

Теорема:средняя линия трапеции равна полусумме её оснований и параллельна им.

Источник

Конспект урока по геометрии. Равенство фигур. Равенство треугольников.7 класс

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Понятие о равенстве фигур

1.1.В геометрии две фигуры, имеющие одинаковые форму и размер называют равными.

1.2. Две геометрические фигуры называются равными, если их можно совместить при наложении.

Из этого определения 1.1. следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и ту же форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры.

Вопрос: Какие отрезки будут считаться равными?

Какие окружности будут считаться равными?

Какие прямоугольники будут считаться равными?

На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону.

Вопрос: Можно ли сравнивать все геометрические фигуры?

Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве.

Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.

Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна.

При изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением).

Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой стрелке или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части.

А.Д. Александров Геометрия 7 класс

А сейчас выполним задание поэтапно:

1.Начертим два равных угла. Этот способ построения угла равного данному углу, мы выбрали не случайно.

Значит, в равных треугольниках соответствующие углы равны.

Проведем прямую а и в

Отметим на них точки А и В, Р и С соответственно так, чтобы расстояние между точками на одной прямой было 4 см.

Источник

Конспект урока по геометрии. Равенство фигур. Равенство треугольников.7 класс

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Понятие о равенстве фигур

1.1.В геометрии две фигуры, имеющие одинаковые форму и размер называют равными.

1.2. Две геометрические фигуры называются равными, если их можно совместить при наложении.

Из этого определения 1.1. следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и ту же форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры.

Вопрос: Какие отрезки будут считаться равными?

Какие окружности будут считаться равными?

Какие прямоугольники будут считаться равными?

На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону.

Вопрос: Можно ли сравнивать все геометрические фигуры?

Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве.

Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.

Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна.

При изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением).

Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой стрелке или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части.

А.Д. Александров Геометрия 7 класс

А сейчас выполним задание поэтапно:

1.Начертим два равных угла. Этот способ построения угла равного данному углу, мы выбрали не случайно.

Значит, в равных треугольниках соответствующие углы равны.

Проведем прямую а и в

Отметим на них точки А и В, Р и С соответственно так, чтобы расстояние между точками на одной прямой было 4 см.

Источник