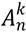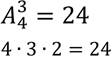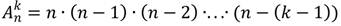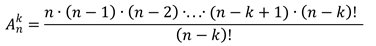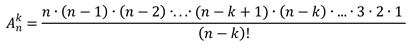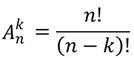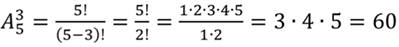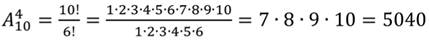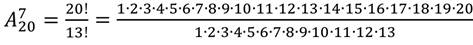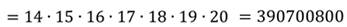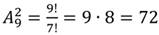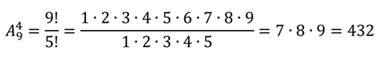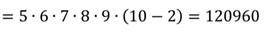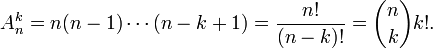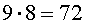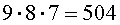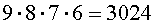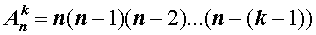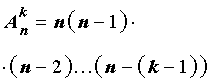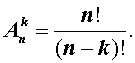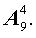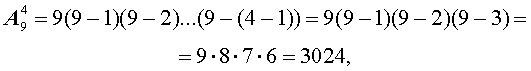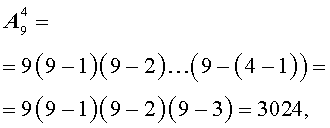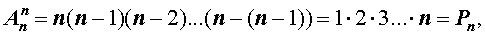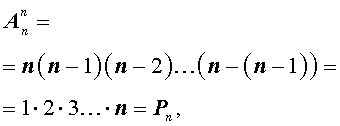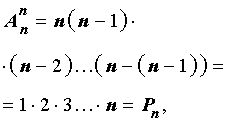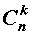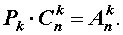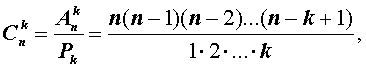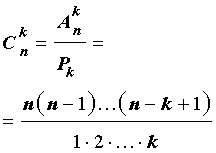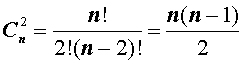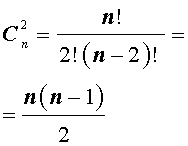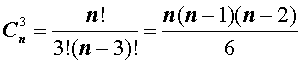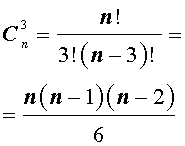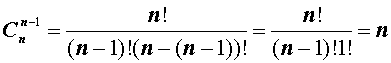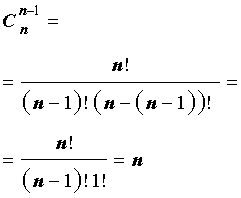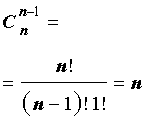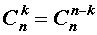Что такое размещение алгебра
Сочетания и размещения — что это такое и в чем разница
Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».
О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.
Сочетания
Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.
Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.
Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.
Сочетания обозначаются следующим образом: С К N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.
Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:
Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.
Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.
Размещения
В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.
Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.
Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).
Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):
Размещений же окажется гораздо больше:
123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.
Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:
Для нашего примера посчитаем количество потенциальных размещений:
Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.
Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.
Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.
Обозначим названия команд буквами: А, Б, В, Г, Д, Е.
Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.
Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.
Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).
Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.
Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.
Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.
Сочетания и размещения: в чем же разница?
И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.
Размещения
Урок 28. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Размещения»
Пусть имеются 4 шара и 3 пустые ячейки. В каждую ячейку можно поместить только по 1 шару.
Для удобства обозначим шары буквами: A, B, C, D.
Выбирая по-разному шары для каждой из ячеек, получим, например, такие тройки:
Размещением из n элементов по k, где k≤n, называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.
Два размещения из n элементов по k считаются различными, если они различаются самими элементами или порядком их следования.
Вернемся к примеру, вычислим количество таких размещений для данного случая, пользуясь правилом комбинаторного умножения:
Получим формулу для вычисления числа размещений из n элементов по k:
Для выбора первого элемента можно взять любой из n элементов, то есть существует n способов. Для выбора второго элемента можем взять любой из n-1 оставшихся элементов, то есть n-1 способов. Третий элемент можно выбрать n-2 способами. И так далее.
Число размещений из n элементов по k можно отыскать по такой формуле:
Преобразуем, умножим и разделим правую часть этого равенства:
Тогда формула числа размещений из n элементов по k примет такой вид:
Стоит обратить внимание на то, что размещения из n элементов по n отличаются только порядком следования элементов, так как каждый из них должен участвовать в размещении.
Тогда получаем, что такое размещение является перестановкой.
1. Вычислить число размещений из 5 элементов по 3.
Воспользовавшись формулой размещений, получим:
Найдем число размещений:
В классе 17 учеников, а на скамейке в парке помещается только 5 человек. Сколькими способами одноклассников можно усадить на скамейку в парке? Порядок рассадки имеет значение.
Найдем количество размещений:
Сколько можно составить телефонных номеров, из 6 цифр каждый, так чтобы все цифры были различны? При этом на первом месте не могут быть цифры 0 и 1.
У нас есть 10 различных цифр. Из них можно составить 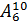
Можно составить 120960 телефонных номеров, состоящих из 6 цифр и не начинающихся 0 и 1.
Размещение (комбинаторика)
В комбинаторике размещением называется расположение «предметов» на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Например, 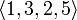
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов <1,2,3>(то есть, совпадают как сочетания).
Содержание
Количество размещений
Количество размещений из n по k, обозначаемое 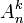
Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из n по k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту 
Размещение с повторениями
Например, количество вариантов 3-x значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно 10 3 = 1000.
Пример алгоритма получения размещений с повторениями для массива объектов на Java
Пример получения размещений с повторениями для списка на Haskell
Ссылки
Полезное
Смотреть что такое «Размещение (комбинаторика)» в других словарях:
Размещение:Комбинаторика — В комбинаторике размещением называется расположение «предметов» на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размещением (из n по k) называется упорядоченный набор … Википедия
РАЗМЕЩЕНИЕ — см. Комбинаторика … Большой Энциклопедический словарь
Размещение — В комбинаторике размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размещением (из n по k) называется… … Википедия
размещение — я; ср. 1. к Разместить размещать и Разместиться размещаться. Р. людей по квартирам. Р. нового оборудования в цехе. Дать время на р. 2. Порядок, система расположения чего л. Р. электродов. Р. производительных сил. Р. промышленных объектов по… … Энциклопедический словарь
РАЗМЕЩЕНИЕ — см. Комбинаторика … Естествознание. Энциклопедический словарь
История комбинаторики — освещает развитие комбинаторики раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные… … Википедия
Сочетание — В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
КОМБИНАТОРНЫЙ АНАЛИЗ — комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
Числа Каталана — числовая последовательность, встречающаяся во многих задачах комбинаторики. Последовательность названа в честь бельгийского математика Каталана, хотя была известна ещё Л. Эйлеру. Первые несколько чисел Каталана: 1, 1, 2, 5, 14, 42, 132, 429, 1430 … Википедия
Комбинаторика: размещения и сочетания
При решении задач по комбинаторике используют следующие важные понятия
 Факториалы Факториалы |
 Перестановки Перестановки |
 Размещения Размещения |
 Сочетания Сочетания |
Размещения
Рассмотрим следующую задачу.
На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует
способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует
способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует
различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можно получить 3024 различных четырехзначных числа.
При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.
В соответствии с определением факториала, формулу (1) можно также записать в виде:
В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.
Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число
В соответствии с формулой (1),
что и было получено в задаче.
смысл которой заключается в следующем.
Сочетания
Число сочетаний из n элементов по k элементов обозначается символом
Таким образом, справедлива формула:
откуда вытекает формула
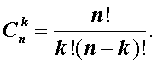 | (2) |
Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):
 | 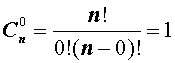 |
 | 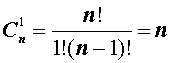 |
 | |
 | 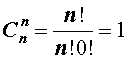 |
В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):
С понятиями факториала числа n и перестановок из n элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.
Размещения
п.1. Размещения без повторений
Например:
Для создания 3-значного пароля используются символы из алфавита <+,*,A. 2>.
Сколько всего паролей без повторения символов можно составить?
По условию n = 5, k = 3. Рассматриваем размещение 5 символов по 3 позициям без повторений: \(\mathrm< A_5^3=\frac<5!><(5-3)!>=5\cdot 4\cdot 3 = 60 >\)
Всего 60 паролей.
Результат можно получить непосредственно из правила произведения. Действительно, на первой позиции – 5 вариантов символов, на второй – 4 оставшихся, на третьей – 3 оставшихся. Итого, по правилу произведения: 5 · 4 · 3 = 60 паролей.
п.2. Размещения с повторениями
п.3. Примеры
Пример 1. Исследуйте различие между перестановкой без повторений и размещением без повторений 〈3,2〉-выборок для трёх разноцветных фишек. Изобразите полученные решения.
Рассматриваем фишки:
1) Для перестановок, 〈3,3〉-выборок, получаем:
 | В каждом ряду – отдельная перестановка. Видно, как образуется факториал. Для каждой отдельной фишки – одна перестановка. Для каждой пары фишек – две перестановки: 2 · 1. Когда добавляем третью, получаем: 3 · 2 · 1 Итого: P3 = 3 · 2 · 1 = 6 перестановок. |
2) Для размещений без повторений, 〈3,2〉-выборок, получаем:
 | В каждом ряду – отдельное размещение. В первом столбце слева – 3 варианта по цвету. Во втором столбце остается только 2 варианта. Итого: \(\mathrm |
Пример 2. Исследуйте перестановки без повторений и размещения для 〈4,3〉 выборок и для 〈4,2〉 выборок без повторений из 4 разноцветных фишек.
Изобразите полученные решения.
Рассматриваем фишки:
 В каждом ряду – отдельная перестановка. Итого: P4=4·3·2·1=24 перестановки. |  В каждом ряду – отдельное размещение. Итого: \(\mathrm |  В каждом ряду – отдельное размещение. Итого: \(\mathrm |
Пример 3. Исследуйте различие между перестановкой с повторениями и размещением с повторениями. Сделайте вывод.
Перестановка с повторениями: сколько слов можно получить, переставляя буквы в слове «МАМА»? Запишите все эти слова в лексикографическом порядке.
Размещение с повторениями: сколько 4-буквенных слов можно получить, используя две буквы: «М» и «А»? Запишите все эти слова в лексикографическом порядке.
1) Для перестановки с повторениями получаем: \begin
Вывод: вариантов для размещения с повторениями получается больше, т.к. они включают слова с одной, тремя и четырьмя «М» и «А». А в перестановки с повторениями входят только слова с двумя «М» и двумя «А».
Пример 4. В базе данных с номерами телефонов содержатся все 7-значные номера.
1) Сколько в книге номеров, в которых цифры не повторяются?
2) Сколько в книге всего номеров?
3) Сколько в книге номеров, у которых 4 последних цифры одинаковые?
4) Сколько в книге номеров, у которых 4 последних цифры одинаковые, а 3 первых цифры отличаются от 4 последних?
1) Цифр – всего 10: