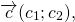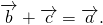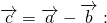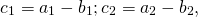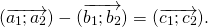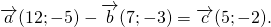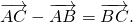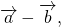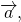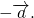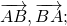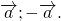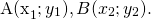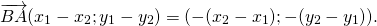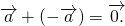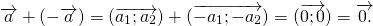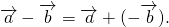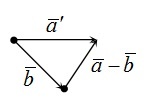Что такое разность векторов в геометрии
Определение разности двух векторов
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
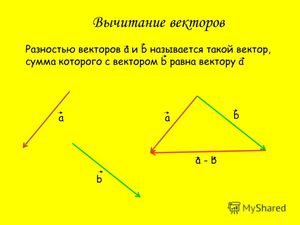
[block >
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.
Вычисление разности графически
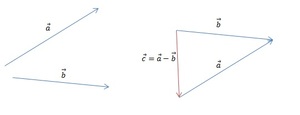
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
[block > Результат операции вычитания показан на рисунке ниже.
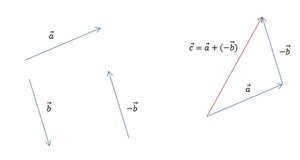
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
Аналогичный расчёт выполняется для CD:
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
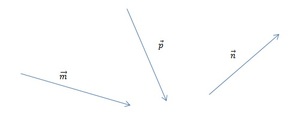
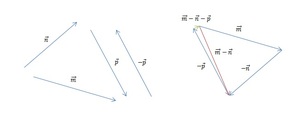
[block > Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
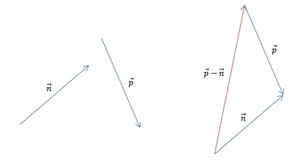
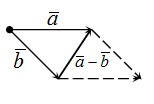
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
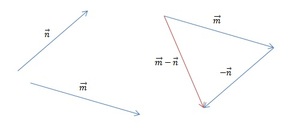
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >
Разность векторов
Разность векторов
— это такой вектор
который в сумме с вектором b даёт вектор a:
На основе определения находим координаты вектора
Как построить разность двух векторов?
Из равенства
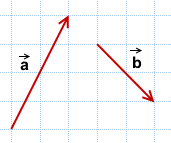
правило построения разности двух векторов
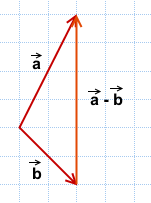
Чтобы построить вектор, равный разности векторов
надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.
Противоположные векторы — это противоположно направленные векторы одинаковой длины.
Вектор, противоположный вектору
Примеры противоположных векторов:
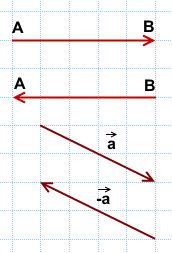
Свойства противоположных векторов:
1) Противоположные векторы имеют противоположные координаты:
2) Сумма противоположных векторов равна нулевому вектору:
2 способ построения разности векторов
Чтобы построить разность векторов
можно к вектору a прибавить вектор, противоположный вектору b:
То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.
Вычитание векторов. Как найти разность векторов
Как сложить и вычесть векторы с помощью онлайн-калькулятора
Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:
В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.
Для наглядности, зададим один вектор точками, а второй – координатами.
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Доказательство.
По определению 2, имеем
Теорема доказана.
Правило параллелограмма разности векторов
Если два неколлинеарных вектора 
и 
имеют общее начало (рис. 3), то разностью этих вектор есть вектор, совпадающий с диагональю параллелограмма, построенного на этих векторах 
и 
, причем начало этой диагонали совпадает с концом вектора 
, а конец – с концом вектора 
.
Если векторы 
и 
заданы своими координатами в некотором базисе: 
, то, чтобы найти координаты их разности 
, необходимо от координат вектора 
отнять соответствующие координаты вектора 
:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
Правило треугольника
Правило параллелограмма
Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:
\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)
\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)
Проиллюстрируем правило многоугольника:
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
Аналогичный расчёт выполняется для CD:
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06. [block Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
[block Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p. [block [block >
Сложение и вычитание векторов
Существование: Имеем два следующих случая:
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Умножение вектора на число
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Вычитание векторов
Как происходит вычитание векторов
Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.
Таким образом, формула разности будет выглядеть так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(\overrightarrow а-\overrightarrow b=\overrightarrow а+\left(-\overrightarrow b\right)\)
\(\overrightarrow а+\left(-\overrightarrow а\right)=0\)
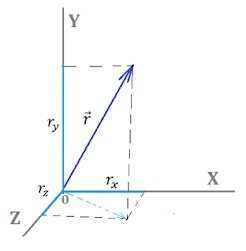
Как производится вычитание векторов по координатам
Проиллюстрируем координатное пространство:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
Правило треугольника
Правило параллелограмма
Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:
\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)
\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)
Проиллюстрируем правило многоугольника:
Примеры задач на понятие разности векторов
Задача 1
Дано
\(\overrightarrow a\;=\left(2;-1\right),\;\overrightarrow b=\left(0;2\right)\)
Найти: \(\overrightarrow с=2\overrightarrow a-3\overrightarrow b\;\)
Решение
\(2\overrightarrow а=2\times\left(2;-1\right)=\left(2\times2;2\times\left(-1\right)\right)=\left(4;-2\right), 3\overrightarrow b=3\times\left(0;2\right)=\left(3\times0;3\times2\right)=\left(0;6\right)\)
Тогда искомый вектор:
\(\overrightarrow с=2\overrightarrow a-3\overrightarrow b=\left(4;-2\right)-\left(0;6\right)=\left(4-0;\;-2-6\right)=\left(4;-8\right)\)
Ответ: \(\overrightarrow с=\left(4;-8\right).\)
Задача 2
Дано
Найти: координаты \(\overrightarrow
Решение
Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.