Что такое разносторонний треугольник 4 класс

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

Источник

Треугольник — определение и основные свойства и виды треугольника

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Виды треугольника

Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

Источник

4 класс. Математика. Виды треугольников.

4 класс. Математика. Виды треугольников.

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

По числу рав­ных сто­рон тре­уголь­ни­ки бы­ва­ют рав­но­сто­рон­ние, рав­но­бед­рен­ные, раз­но­сто­рон­ние.

Рав­но­бед­рен­ным на­зы­ва­ет­ся тре­уголь­ник, у ко­то­ро­го две сто­ро­ны равны (рис. 7).

Рис. 7. Рав­но­бед­рен­ный тре­уголь­ник

Эти сто­ро­ны на­зы­ва­ют­ся бо­ко­вы­ми, тре­тья сто­ро­на – ос­но­ва­ни­ем. В рав­но­бед­рен­ном тре­уголь­ни­ке углы при ос­но­ва­нии равны.

Рав­но­бед­рен­ные тре­уголь­ни­ки бы­ва­ют ост­ро­уголь­ны­ми и ту­по­уголь­ны­ми (рис. 8).

Рис. 8. Ост­ро­уголь­ный и ту­по­уголь­ный рав­но­бед­рен­ные тре­уголь­ни­ки

Рав­но­сто­рон­ним на­зы­ва­ет­ся тре­уголь­ник, у ко­то­ро­го все три сто­ро­ны равны (рис. 9).

Рис. 9. Рав­но­сто­рон­ний тре­уголь­ник

В рав­но­сто­рон­нем тре­уголь­ни­ке все углы равны. Рав­но­сто­рон­ние тре­уголь­ни­ки все­гда ост­ро­уголь­ные.

Раз­но­сто­рон­ним на­зы­ва­ет­ся тре­уголь­ник, у ко­то­ро­го все три сто­ро­ны имеют раз­ную длину (рис. 10).

Рис. 10. Раз­но­сто­рон­ний тре­уголь­ник

Вы­пол­ни­те за­да­ние. Рас­пре­де­ли­те дан­ные тре­уголь­ни­ки на три груп­пы (рис. 11).

Рис. 11. Ил­лю­стра­ция к за­да­нию

Сна­ча­ла рас­пре­де­лим по ве­ли­чине углов.

Ост­ро­уголь­ные тре­уголь­ни­ки: № 1, № 3.

Пря­мо­уголь­ные тре­уголь­ни­ки: № 2, № 6.

Ту­по­уголь­ные тре­уголь­ни­ки: № 4, № 5.

Эти же тре­уголь­ни­ки рас­пре­де­лим на груп­пы по числу рав­ных сто­рон.

Раз­но­сто­рон­ние тре­уголь­ни­ки: № 4, № 6.

Рав­но­бед­рен­ные тре­уголь­ни­ки: № 2, № 3, № 5.

Рав­но­сто­рон­ний тре­уголь­ник: № 1.

По­ду­май­те, из ка­ко­го куска про­во­ло­ки сде­ла­ли каж­дый тре­уголь­ник (рис. 12).

Рис. 12. Ил­лю­стра­ция к за­да­нию

Можно рас­суж­дать так.

Пер­вый кусок про­во­ло­ки раз­де­лен на три рав­ные части, по­это­му из него можно сде­лать рав­но­сто­рон­ний тре­уголь­ник. На ри­сун­ке он изоб­ра­жен тре­тьим.

Вто­рой кусок про­во­ло­ки раз­де­лен на три раз­ные части, по­это­му из него можно сде­лать раз­но­сто­рон­ний тре­уголь­ник. На ри­сун­ке он изоб­ра­жен пер­вым.

Тре­тий кусок про­во­ло­ки раз­де­лен на три части, где две части имеют оди­на­ко­вую длину, зна­чит, из него можно сде­лать рав­но­бед­рен­ный тре­уголь­ник. На ри­сун­ке он изоб­ра­жен вто­рым.

Се­год­ня на уроке мы по­зна­ко­ми­лись с раз­лич­ны­ми ви­да­ми тре­уголь­ни­ков.

Источник

Геометрическая фигура: треугольник

В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.

Определение треугольника

Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.

Углы можно, также, обозначать с помощью специального знака “∠“:

Классификация треугольников

В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:

1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.

2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

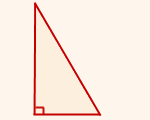
3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

4. Разносторонний – треугольник, у которого все стороны имеют разную длину.

5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

Свойства треугольника

1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:

Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.

2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.

3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.

Примеры задач

Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.

Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.

Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4

Источник

Что такое разносторонний треугольник

Здравствуйте!
Подскажите, что такое разносторонний треугольник? Есть ли у него какие-то свойства? Может приведете в пример какую-либо задачу с участием разностороннего треугольника?
Спасибо за помощь!

Треугольник называется разносторонним, потому что все его стороны разные по длине.
Разносторонние треугольники, как и другие виды треугольников, имеют свои свойства:

Пример 1.
Стороны разностороннего треугольника равны 13, 24 и 36 см. Определим, к кому виду треугольников (к тупоугольному, остроугольному или прямоугольному) он относится?

Решение.
Представим, что заданный треугольник является прямоугольным. В таком случае его меньшие стороны 13 и 24 см являются катетами, а сторона 36 см — гипотенузой. Следовательно, будет справедлива теорема Пифагора:
(см).
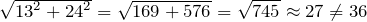
Таким образом, наше предположение, что данный треугольник является прямоугольным — не верно.
Чтобы получить данный треугольник, необходимо его сторону увеличить на 36—27=9 см. Соответственно, если увеличить сторону, то увеличится и угол (по предположению — прямой), который находится против нее. Это значит, что заданный треугольник является тупоугольным.

Ответ. Заданный треугольник — тупоугольный.

Источник