Что такое ребра тетраэдра

Тетраэдр.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

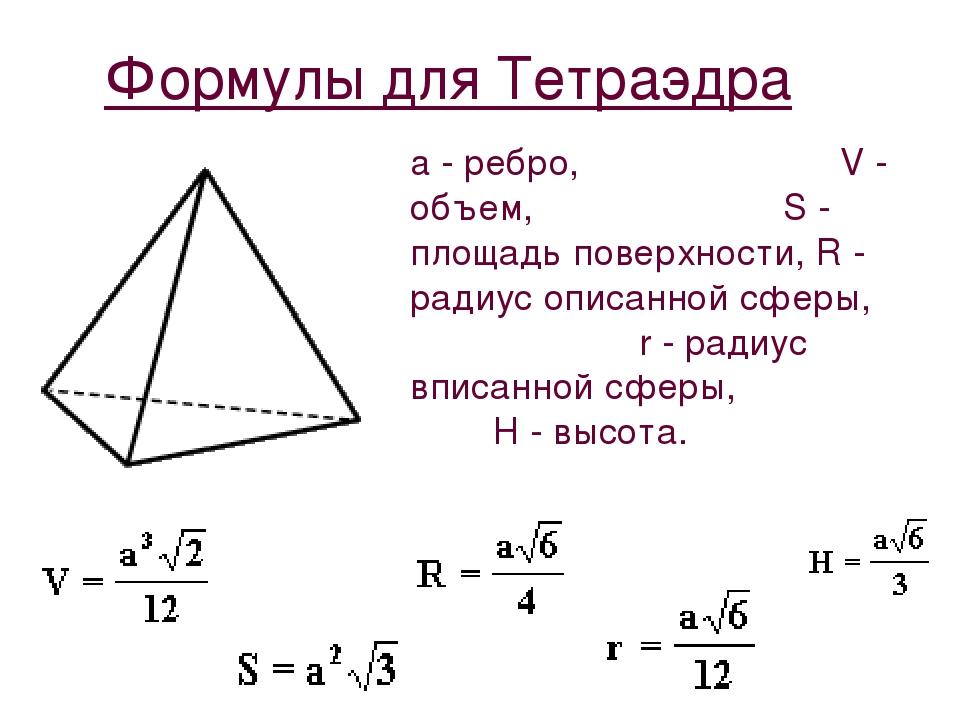
Формулы для определения элементов тетраэдра.

Высота тетраэдра:

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Основные формулы для правильного тетраэдра:

Источник

Тетраэдр

Тетраэдр имеет следующие характеристики:

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Видео. Тетраэдр из набора «Волшебные грани»

Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал Оригами)

вращение готового многогранника:

Видео. Вращение всех правильных многогранников

Источник

Свойства тетраэдра, виды и формулы

Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.

Элементы четырехгранника

Вам будет интересно: Петрозаводский педагогический колледж: стать специалистом заочно

Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.

Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.

Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.

Свойства тетраэдра

1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.

3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.

Виды тетраэдра

Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:

Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.

Формулы четырехгранника

Высота тетраэдра равна произведению корня из 2/3 и длины ребра.

Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.

Остальные формулы для расчета площади и радиусов окружностей представлены выше.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №7. Тетраэдр и параллелепипед

Перечень вопросов, рассматриваемых в теме

Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.

Сечением поверхности геометрических тел называется – плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Учебник Геометрия 10-11 кл.– М.: Просвещение, 2014.

Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.

Открытый электронный ресурс:

Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru

Теоретический материал для самостоятельного изучения

В дельнейшем несколько уроков нашего курса будет посвящены многогранникам- поверхностям геометрических тел, составленным из многоугольников. Но до более подробного изучения многогранников мы познакомимся с двумя из них- тетраэдром и параллелепипедом. Нам данные тела дадут возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей.

Давайте вспомним, что мы понимали под многоугольником в планиметрии. Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, либо как часть плоскости, ограниченную этой линией, включая ее саму.

Мы будем использовать второе толкование многоугольника при рассмотрении поверхностей и тел в пространстве. При таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.

Давайте рассмотрим изображенную фигуру и ответим на несколько вопросов.

Итак, поверхность данной фигуры состоит из четырёх треугольников DАВ, DВС, DАС и АВС.

Мы с вами выяснили из элементов состоит наша фигура тетраэдр. Теперь сформулируем определение.

Определение. Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Говорят, что рёбра АD и ВС, АВ и CD, и т.д.- противоположные.

Изображается тетраэдр обычно так (рис. 1).

Рисунок 1 – изображение тетраэдра.

Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. И тетраэдр тому доказательство. Так же мы можем наблюдать тетраэдр в повседневной жизни (рис. 2).

Форма пакета молока

Прежде чем начать изучать параллелепипед вспомним определение параллелограмма и его свойства.

Определение. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом (рис. 3).

Рисунок 3 – параллелограмм

1. Противоположные стороны параллелограмма равны:

2. Противоположные углы параллелограмма равны:

3. Диагонали параллелограмма точкой пересечения делятся пополам:

треугольники ABC и CDA равны.

6. Накрест лежащие углы при диагонали равны:

А теперь перейдем к параллелепипеду.

Рассмотрим два равных параллелограмма ABCD и A₁B₁C₁D₁, расположенных в параллельных плоскостях так, что отрезки AA_1, BB_1, CC₁ и DD₁ параллельны.

Давайте рассмотрим изображенную фигуру (рис. 4).

Рисунок 4 – параллелепипед и его диагонали

АВСDA₁B₁C₁D₁: поверхность, составленная из двух равных параллелограммов АВСD и A₁B₁C₁D₁, лежащих в параллельных плоскостях и четырёх параллелограммов.

Определение. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда:
A₁C, D₁B, AC₁, DB₁.

Параллелепипед – слово греческого происхождения, параллел – идущий рядом, епипед – плоскость.

Определение.Параллелепипед- этошестигранник с параллельными и равными противоположными гранями.

Следует отметить, что многоугольник в пространстве представляет собой плоскую поверхность, а тетраэдр и параллелепипед – поверхности, составленные из плоских поверхностей (соответственно треугольников и параллелограммов).

Способы изображения параллелепипеда

Параллелепипед, в основании которого лежит ромб

Параллелепипед, в основании которого лежит квадрат

Параллелепипед,в основании которого лежит прямоугольник или параллелограмм

Параллелепипед, у которого все грани — равные квадраты

Можно сделать вывод, что параллелепипеды делятся на (рис. 5)

Рисунок 5 – виды параллелепипедов

В параллелепипеде ABCDA₁B₁C₁D₁грани ВВ₁С₁С и AA₁D₁D параллельны (рис. 6), потому что две пересекающиеся прямые ВВ₁ и В₁С₁ одной грани параллельны двум пересекающимся прямым АА₁ и A₁D₁ другой; эти грани и равны, так как В₁С₁ = A₁D₁, В₁В= А₁А (как противоположные стороны параллелограммов) и ∟ ВВ₁С₁= ∟АA₁D₁.

Рисунок 6 – чертеж к доказательству свойства 1

Возьмём какие-нибудь две диагонали, например АС₁ и ВD₁, и проведём вспомогательные прямые АD₁ и ВС₁ (рис. 7).

Так как рёбра АВ и D₁С₁ соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD₁С₁В есть параллелограмм, в котором прямые С₁А и ВD₁ —диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам.

Возьмём теперь одну из этих диагоналей, например АС₁, с третьей диагональю, положим, с В₁D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B₁D и АС₁ и диагонали АС₁ и BD₁(которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали
АС₁. Наконец, взяв эту же диагональ АС₁ с четвёртой диагональю А₁С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС₁. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.

Рисунок 7 – чертеж к доказательству свойства 2

Задачи на построение сечений.

Взаимное расположение многогранника и секущей плоскости:

Фигуры, которые получаются в результате сечения:

Один из методов построения сечений, который мы рассмотрим- метод следа.

Рассмотрим метод следов, применяемый при построении сечений многогранников, а именно при построении сечения куба плоскостью.

Что такое метод следов? При построении сечений многогранников в качестве вспомогательной прямой часто используется след секущей плоскости (в плоскости грани, удобной для рассмотрения). Такой метод построения сечений называется методом следа.

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (рис. 8).

Рисунок 8 –чертеж к задаче №1

Основные правила построения сечений методом следа:

То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.

Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.

Рисунок 9 – чертеж к задаче №2

Решение:
Для решения построим вспомогательную плоскость DМN (рис. 10). Пусть прямая DМ пересекает прямую АВ в точке К. Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.

Примеры и разбор решения заданий тренировочного модуля

Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.

Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС (рис. 11). В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.

Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р₁ и Р₂. Соединяем Р₁ и М и на продолжении получаем точку М₁. Соединяем точку Р₂ и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.

Рисунок 10 – чертеж к примеру 1 (первый случай)

Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС (рис. 12). Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р₁Р₂, тогда прямая Р₁Р₂ параллельна данной прямой MN.

Рисунок 11 – чертеж к примеру 1 (второй случай)

Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым.

Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N (рис. 13).
По теореме (о параллельных прямых) линия пересечения параллельна SB.
В плоскость SBC через т. N проходит NQ||SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. M (прямая MP). По теореме (о параллельных прямых) линия пересечения параллельна SB.

следовательно, PM||NQ.Утверждение доказано.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 16. Правильные многогранники

Перечень вопросов, рассматриваемых в теме:

Правильный многогранник – выпуклый многогранник, все грани которого равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Правильный тетраэдр – многогранник, составленный из четырех равносторонних треугольников.

Правильный октаэдр – многогранник, составленный из восьми равносторонних треугольников.

Правильный икосаэдр – многогранник, составленный из двадцати равносторонних треугольников.

Куб (гексаэдр) – многогранник, составленный из шести квадратов.

Правильный додекаэдр – многогранник, составленный из двенадцати правильных пятиугольников.

Точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.

Точки А и А1 называются симметричными относительно прямой а, если прямая а проходит через середину отрезка АА1 и перпендикулярна этому отрезку.

Точки Аи А1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна этому отрезку.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2009. – 368 с.: ил. (128 с. – 131 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. (68 с. – 73 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Теоретический материал для самостоятельного изучения

Также нам уже знаком правильный тетраэдр.

Заметьте, что правильный тетраэдр и правильная треугольная пирамида – это различные многогранники!

Напомним, что пирамида называется правильной, если в основании лежит правильный многоугольник, а основание высоты совпадает с центром многоугольника. Таким образом, в правильной треугольной пирамиде боковые ребра равны друг другу, но могут быть не равны ребрам основания пирамиды, а в правильном тетраэдре все ребра равны.

Правильных многогранников существует всего 5. Перечислим их.

Правильный тетраэдр – многогранник, составленный из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников, значит сумма плоских углов при каждой вершине равна 180.

Правильный октаэдр – многогранник, составленный из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников, значит, сумма плоских углов при каждой вершине равна 240.

Куб (гексаэдр) – многогранник, составленный из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма плоских углов при

каждой вершине равна 270.

Правильный икосаэдр – многогранник, составленный из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников, значит, сумма плоских углов при каждой равна 300.

Рисунок 4 – Правильный икосаэдр

Правильный додекаэдр – многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников, значит, сумма плоских углов при каждой равна 324.

Рисунок 5 – Правильный додекаэдр

Докажем, что правильных многогранников существует ровно 5, то есть что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.

По этой причине каждая вершина правильного многогранника может быть вершиной либо трех, либо четырех, либо пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников.

Симметрия в пространстве

Одно из интересных свойств правильных многогранников – это элементы симметрии.

Прежде чем мы их выделим давайте определим симметрию в пространстве.

Вам уже знакома симметрия из курса планиметрии. Там мы рассматривали фигуры симметричные относительно прямой и точки. В стереометрии же рассматривают симметрию относительно точки, прямой и плоскости.

Будем говорить, что точки А и А1 симметричны относительно точки О (рис. 6), если О – середина отрезка АА1. В таком случае О будет являться центром симметрии и будет симметрична сама себе.

Рисунок 6 – Центральная симметрия

Точки А и А1 называются симметричными относительно прямой а, если прямая а проходит через середину отрезка АА1 и перпендикулярна к этом отрезку (рис. 7). Прямая а называется осью симметрии, а каждая ее точка считается симметричной самой себе.

Рисунок 7 – Осевая симметрия

Точки АА1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 8). Плоскость α называется плоскостью симметрии, а каждая ее точка считается симметричной самой себе.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Рисунок 8 – Зеркальная симметрия

Рисунок 9 – Элементы симметрии куба

Примером фигуры, обладающей и центральной, и осевой и зеркальной симметрией является куб (рис. 9).

Фигура может иметь один или несколько центров (осей, плоскостей) симметрии. Так, например, у куба один центр симметрии и несколько осей и плоскостей симметрии.

В геометрии центр, ось и плоскость симметрии многогранника называют элементами симметрии многогранников.

С симметрией мы часто можем встретиться в природе, архитектуре, быту.

Например, многие кристаллы имеют центр ось или плоскость симметрии.

Многие здания симметричны относительно плоскости. Примером такого здания является здание Московского государственного университета.

Рисунок 10 – Здание Московского государственного университета

Примеры и разбор решения заданий тренировочного модуля

№1 Выберите неверные утверждения

1) правильный додекаэдр состоит из 8 правильных треугольников

2) тетраэдр имеет 4 грани

3) гексаэдр состоит из шести параллелограммов

4) правильный октаэдр состоит из правильных пятиугольников

Утверждение под номером 1 неверно, так как название «додекаэдр» с греческого означает «двенадцать граней». В действительности, додекаэдр состоит из двенадцати правильных пятиугольников.

Утверждение 2 верно. Тетраэдр с греческого означает 4 грани и состоит тетраэдр из 4-х треугольников.

Гексаэдр, он же куб состоит из квадратов, которые в свою очередь являются параллелограммами, поэтому утверждение 3 верно.

С греческого «октаэдр» означает 8 граней, состоять в таком случае из пятиугольников он не может. Октаэдр состоит из восьми треугольников. Утверждение 4 неверно.

№ 2 Установите соответствие между правильными многогранниками и их развертками.

1) 2) 3) 4)

5) 6)

7) 8)

9) 10)

Для выполнения этого задания необходимо понять, из каких многоугольников составлен многогранник.

Итак, куб состоит из квадратов. Единственная развертка, состоящая из квадратов это развертка под номером 6. Проверить себя можно и мысленно сложив из развертки кубик.

Многогранник под номером 2 – тетраэдр, состоит из четырех треугольников. Поэтому ему будет соответствовать развертка под номером 7. Мысленно сложите из развертки тетраэдр.

Октаэдр состоит из 8 треугольников, в этом несложно убедиться исходя из изображения. Развертка под номером 8 как раз состоит из 8 треугольников.

Многогранник под номером 4 состоит также из треугольников, а единственная развертка, состоящая из треугольников, осталась под номером 10. Попробуйте вырезать такую развертку из бумаги и собрать свой икосаэдр!

Многогранник под номером 5 состоит из пятиугольников. Оставшаяся развертка 9 тоже состоит из пятиугольников. Осталось проверить, что количество совпадает.

Источник