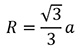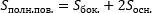Что такое ребро треугольной призмы

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Правильная треугольная призма

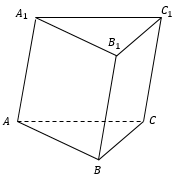
Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.

Основания призмы являются равными правильными треугольниками.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности треугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной треугольной призмы:

Правильная треугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной треугольной призмы:

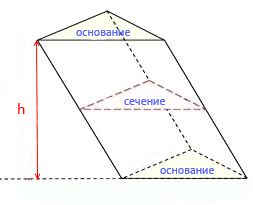
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.

Источник

Ребра треугольной призмы

Свойства

Зная стороны оснований треугольной призмы и боковые ребра, можно вычислить все необходимые параметры треугольной призмы. Равносторонний треугольник в основании позволяет найти высоту основания, равную ребру основания, деленному на корень из двух. Радиусы окружностей, которые могут быть вписаны и описаны около оснований треугольной призмы, также можно найти по формулам для равностороннего треугольника. h=a/√2 r=a/(2√3) R=a/√3

Чтобы найти диагональ боковой грани призмы, нужно знать не только сторону ее основания, но и боковое ребро, тогда диагональ станет гипотенузой в прямоугольном треугольнике из бокового ребра и ребра основания. d=√(a^2+b^2 )

Периметр треугольной призмы складывается из шести сторон оснований, по три на каждое, и трех боковых ребер. Площадь основания треугольной призмы равна площади равностороннего треугольника, а площадь боковой поверхности – трем площадям прямоугольников со сторонами ребром основаниям и боковым ребром. Чтобы посчитать площадь полной поверхности треугольной призмы, нужно сложить две площади основания и площадь боковой поверхности. P=3(2a+b) S_(осн.)=(√3 a^2)/4 S_(б.п.)=3ab S_(п.п.)=3ab+(√3 a^2)/2

Чтобы вычислить объем треугольной призмы, как и любого другого объемного тела с двумя основаниями, необходимо площадь основания умножить на высоту тела/боковое ребро призмы. V=S_(осн.) b=(√3 a^2 b)/4

Вокруг любой треугольной призмы можно описать сферу, ее радиус будет равен квадратному корню из суммы квадрата радиуса описанной вокруг основания окружности и квадрата половины бокового ребра призмы, которые путем алгебраических преобразований приводят к квадратному корню из пяти шестых, умноженному на сторону основания. R_1=√(5/6) a

В треугольную призму можно вписать сферу тогда и только тогда, когда половина ее высоты равна радиусу вписанной в основание окружности, в таком случае радиус вписанной в треугольную призму сферы будет равен радиусу вписанной в основание окружности (половине бокового ребра). r_1=r

Источник

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

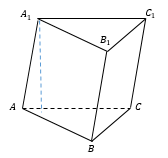
Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

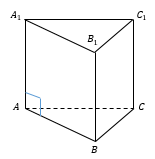
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

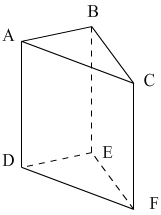
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Перечень вопросов, рассматриваемых в теме:

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

Рассмотрим два равных многоугольника А₁А₂. А_n и В₁В₂. В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂. А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

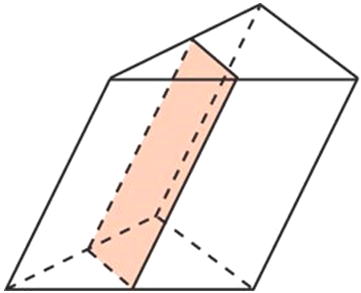
Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С 2 =АА₁ 2 +АС 2 (1).

Так как в основании прямоугольник, то ВС=АD.

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.

Примеры и разбор решения заданий тренировочного модуля

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Источник