Что такое регрессия в машинном обучении
Регрессия в машинном обучении: оптимальный алгоритм
Регрессия используется в ML. Рассмотрим несколько алгоритмов и определим, как их использовать, исходя из преимуществ и недостатков.
Сталкиваясь с какой-либо проблемой в ML, помните, что есть множество алгоритмов, позволяющих её решить. Однако не существует такого универсального алгоритма, который подходил бы под все случаи и решал абсолютно все проблемы.
Выбор алгоритма строго зависит от размера и структуры ваших данных. Таким образом, выбор правильного алгоритма может быть неясен до тех пор, пока мы не проверим возможные варианты и не наткнёмся на ошибки.
Но каждый алгоритм обладает как преимуществами, так и недостатками, которые можно использовать в качестве руководства для выбора наиболее подходящего под ситуацию.
Линейная и полиномиальная регрессия
Начнём с простого. Одномерная (простая) линейная регрессия – это метод, используемый для моделирования отношений между одной независимой входной переменной (переменной функции) и выходной зависимой переменной. Модель линейная.
Более общий случай – множественная линейная регрессия, где создаётся модель взаимосвязи между несколькими входными переменными и выходной зависимой переменной. Модель остаётся линейной, поскольку выходное значение представляет собой линейную комбинацию входных значений.
Также стоит упомянуть полиномиальную регрессию. Модель становится нелинейной комбинацией входных переменных, т. е. среди них могут быть экспоненциальные переменные: синус, косинус и т. п. Модели регрессии можно обучить с помощью метода стохастического градиента.
Преимущества:
Недостатки:
Нейронные сети
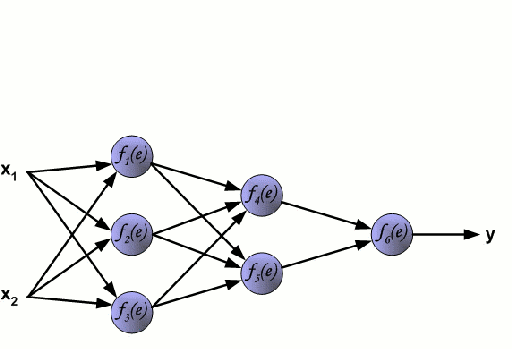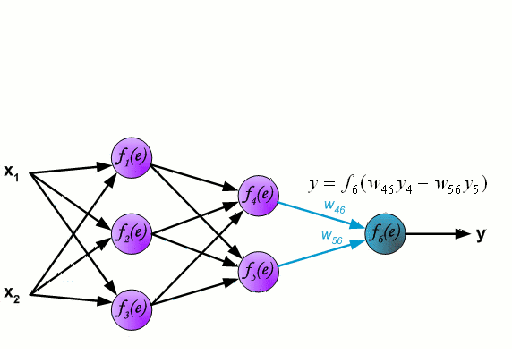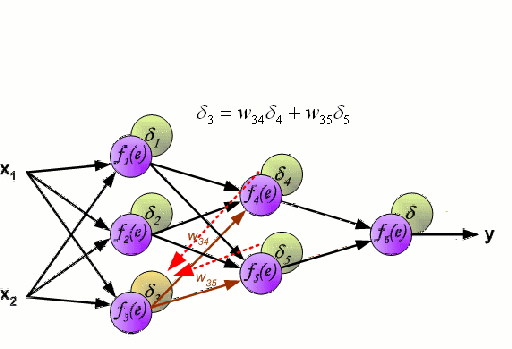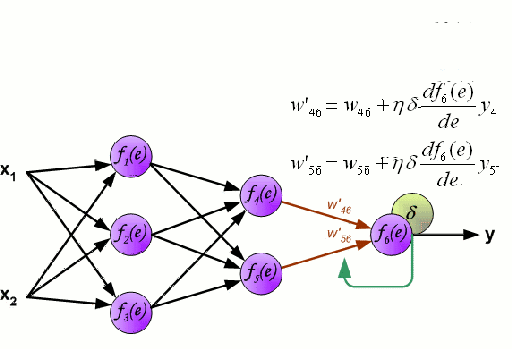
Нейронная сеть состоит из взаимосвязанных групп узлов, называемых нейронами. Входные данные передаются в эти нейроны в виде линейной комбинации со множеством переменных. Значение, умножаемое на каждую функциональную переменную, называется весом. Затем к этой линейной комбинации применяется нелинейность, что даёт нейронной сети возможность моделировать сложные нелинейные отношения. Чаще всего нейросети бывают многослойными: выход одного слоя передается следующему так, как описано выше. На выходе нелинейность не применяется.
Нейронные сети тренируются с помощью метода стохастического градиента и алгоритма обратного распространения ошибки.
Преимущества:
Недостатки:
Дерево принятия решений и Случайный лес
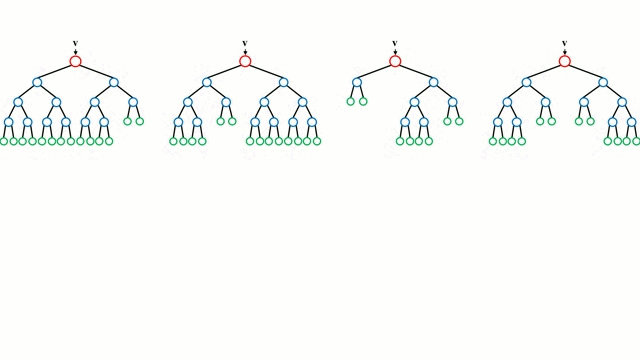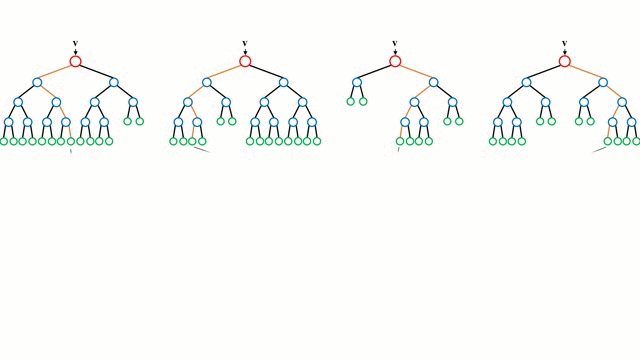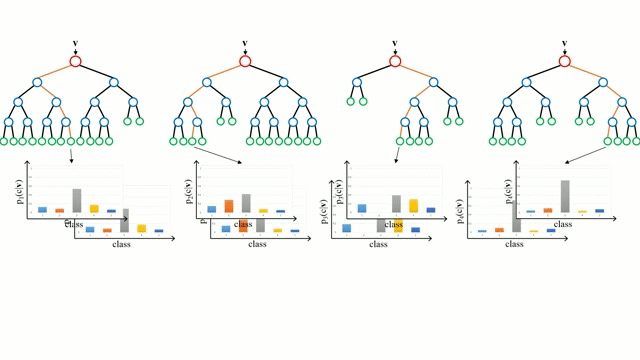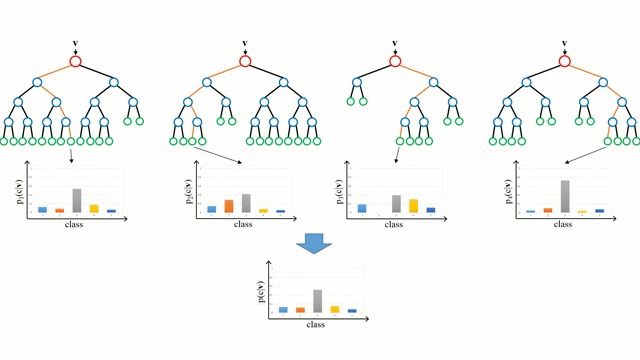
Начнём с простого случая. Дерево принятия решений – это представления правил, находящихся в последовательной, иерархической структуре, где каждому объекту соответствует узел, дающий решение. При построении дерева важно классифицировать атрибуты так, чтобы создать “чистые” узлы. То есть выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов в каждом из этих множеств было как можно меньше.
“Случайные лес” – совокупность деревьев принятия решений. Входной вектор проходит через несколько деревьев решений. Для регрессии выходное значение всех деревьев усредняется; для классификации используется схема голосования для определения конечного класса.
5 алгоритмов регрессии в машинном обучении, о которых вам следует знать

Источник: Vecteezy
Да, линейная регрессия не единственная
Быстренько назовите пять алгоритмов машинного обучения.
Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты. Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.
Команда Mail.ru Cloud Solutions перевела статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.
1. Нейросетевая регрессия
Теория
Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.
Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).

Источник. Свободное изображение
Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.
Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.
Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.
Реализация
Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).
model = Sequential()
model.add(Dense(100, input_dim=3, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation=’softmax’))
#IMPORTANT PART
model.add(Dense(1, activation=’linear’))
Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.
Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.
2. Регрессия дерева решений
Теория
Деревья решений в классификации и регрессии очень похожи, поскольку работают путем построения деревьев с узлами «да/нет». Однако в то время как конечные узлы классификации приводят к одному значению класса (например, 1 или 0 для задачи бинарной классификации), деревья регрессии заканчиваются значением в непрерывном режиме (например, 4593,49 или 10,98).

Иллюстрация автора
Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.
Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.
Реализация
Регрессия дерева решений может быть легко создана в sklearn :
Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.
3. Регрессия LASSO
Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).
Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).

Иллюстрация автора. Упрощенная визуализация процесса сжатия
Процесс сжатия добавляет регрессионным моделям несколько преимуществ:
Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.
Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.
Реализация
В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.
4. Гребневая регрессия (ридж-регрессия)
Теория
Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).
Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.

Сравнение ошибок в регрессии лассо (слева) и гребневой регрессии (справа). Поскольку гребневая регрессия использует регуляризацию L2, ее площадь напоминает круг, тогда как регуляризация лассо L1 рисует прямые линии. Свободное изображение. Источник
В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.
Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.
Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.
Реализация
Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.
5. Регрессия ElasticNet
Теория
ElasticNet стремится объединить лучшее из гребневой регрессии и регрессии лассо, комбинируя регуляризацию L1 и L2.
Лассо и гребневая регрессия представляют собой два различных метода регуляризации. В обоих случаях λ — это ключевой фактор, который контролирует размер штрафа:
9 ключевых алгоритмов машинного обучения простым языком
Машинное обучение (МО) уже меняет мир. Google использует МО предлагая и показывая ответы на поисковые запросы пользователей. Netflix использует его, чтобы рекомендовать вам фильмы на вечер. А Facebook использует его, чтобы предложить вам новых друзей, которых вы можете знать.
Машинное обучение никогда еще не было настолько важным и, в тоже время, настолько трудным для изучения. Эта область полна жаргонов, а количество разных алгоритмов МО растет с каждым годом.
Эта статья познакомит вас с фундаментальными концепциями в области машинного обучения. А конкретнее, мы обсудим основные концепции 9ти самых важных алгоритмов МО на сегодняшний день.
Система рекомендаций(Recommendation system)
Для построения полноценной системы рекомендаций с 0, требуются глубокие знания в линейной алгебре. Из-за чего, если вы никогда не изучали эту дисциплину, вам может быть сложно понять некоторые концепции этого раздела.
Но не беспокойтесь — scikit-learn библиотека Python позволяет довольно просто построить СР. Так что вам не потребуется таких уж глубоких познаний в линейной алгебре, чтобы построить рабочую СР.
Как работает СР?
Существует 2 основных типа система рекомендаций:
Коллаборативная фильтрация СР предоставляет рекоммендации, основанные на знаниях о том как пользователь взаимодействует с элементами(*примечание: за основу взяты взаимодействия с элементами других пользователей, схожих по поведению с данным пользователем). Другими словами, они используют «мудрость толпы»(отсюда и «коллаборативный» в названии метода).
В реальном мире коллаборативная фильтрация СР куда более распространена, нежели основанная на контенте система. Это обусловлено, преимущественно, потому что они обычно дают результат лучше. Некоторые специалист также находят коллаборативную систему более простой для понимания.
Коллаборативная фильтрация СР также обладает уникальной особенностью, которой нет в основанной на контенте ситстеме. А именно, у них есть способность обучаться фичам самостоятельно.
Это значит, что они могут даже начать определять подобие в элементах, основываясь на свойствах или чертах, которые вы даже не предоставляли для работы этой системе.
Существует 2 подкатегории коллаборативной фильтрации:
Подведем итог
Вот краткое резюме того, что мы узнали о системе рекомендаций в данной статье:
Линейная регрессия (Linear Regression)
Линейная регрессия используется для предсказаний некоторого значения y основываясь на некотором множестве значений x.
История линейной регрессии
Линейная регрессия(ЛР) была изобретена в 1800 году Френсисом Гальтоном. Гальтон был ученым, изучающим связь между родителями и детьми. А конкретнее, Гальтон исследовал связь между ростом отцов и ростом их сыновей. Первым открытием Гальтона стал тот факт, что рост сыновей, как правило, был приблизительно таким же как рост их отцов. Что не удивительно.
Позднее, Гальтон открыл нечто более интересное. Рост сына, как правило, был ближе к средне-общему росту всех людей, чем к росту его собственного отца.
Гальтон даль этому феномену название — регрессия. В частности, он сказал: » Рост сына имеет тенденцию к регрессии(или к смещению в направлении) среднего роста».
Это привело к целой области в статистике и машинном обучении под названием регрессия.
Математика линейной регрессии
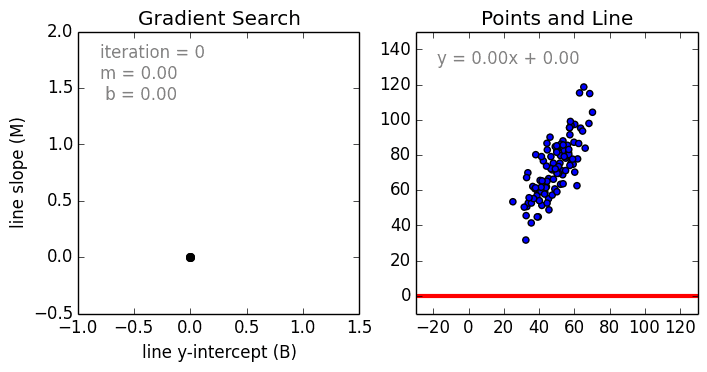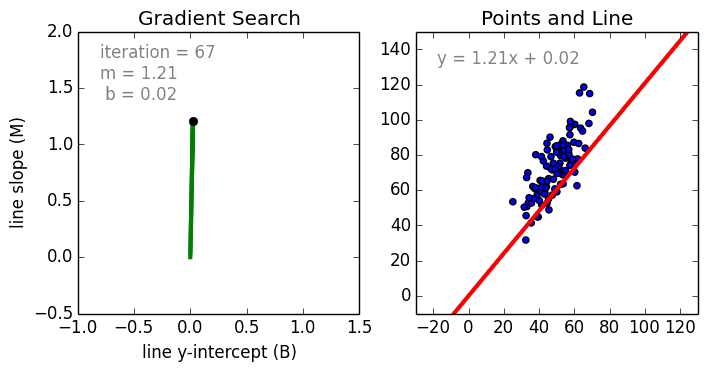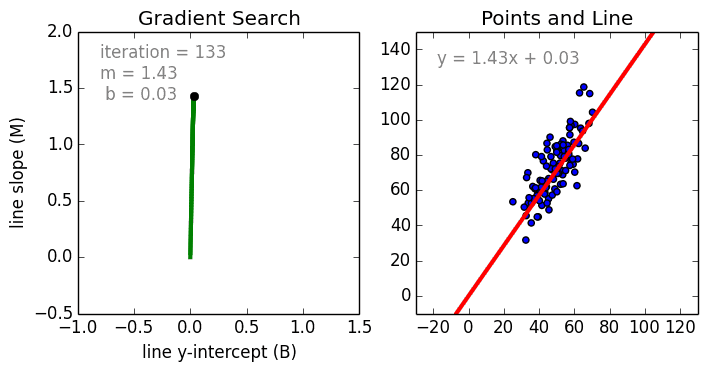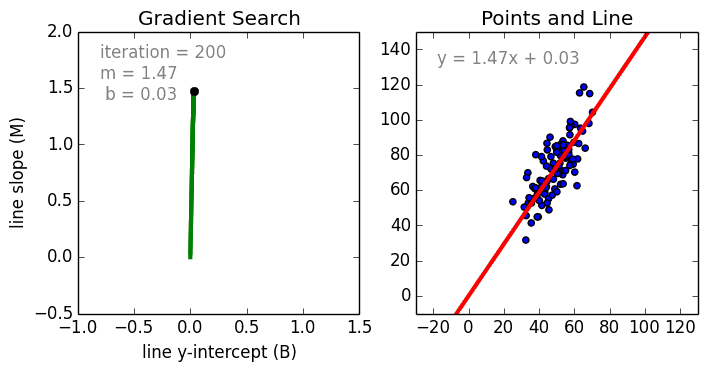
В процессе создания регрессионной модели, все что мы пытаемся сделать — это нарисовать линию настолько близко к каждой точке из набора данных, на сколько это возможно.
Типичный пример такого подхода — «метод наименьших квадратов» линейной регрессии, с помощью которого рассчитывают близость линии в направлении верх-низ.
Пример для иллюстрации:
Когда вы создаете регрессионную модель, ваш конечный продукт — это уравнение, с помощью которого вы можете предсказать значения y для значения x без того чтобы знать значение y наперед.
Логистическая регрессия (Logistic Regression)
Логистическая регрессия схожа с линейной, за исключением того факта, что вместо вычисления значения у, она оценивает к какой категории принадлежит данная точка данных.
Что такое логистическая регрессия?
Логистическая регрессия — это модель машинного обучения, использующаяся для решения задач классификации.
Ниже представлено несколько примеров классификационных задач МО:
Логистическая регрессия хорошо подходит для решения задач двоичной классификации — мы просто назначаем разным категориям значения 0 и 1 соответственно.
Зачем нужна логистическая регрессия? Потому что вы не можете использовать линейную регрессию для прогнозов по двоичной классификации. Она просто не будет подходить, так как вы будете пытаться провести прямую линию через набор данных с двумя возможными значениями.
Это изображение может помочь понять почему линейная регрессия плохо подходит для двоичной классификации:
На этом изображении ось у представляет вероятность того, что опухоль является злокачественной. Значения 1-у представляет вероятность, что опухоль доброкачественная. Как вы можете видеть, модель линейной регрессии очень плохо срабатывает для предсказания вероятности для большинства наблюдений в наборе данных.
Вот почему логистическая регрессионная модель полезна. У нее есть изгиб к линии лучшего соответсвия, что делает ее(модель) гораздо более подходящей для предсказаний качественных(категорийных) данных.
Вот пример, который иллюстрирует сравнение линейной и логистической регрессионых моделей на одних и техже данных:
Сигмоида (The Sigmoid Function)
Причина по которой логистическая регрессия имеет изгиб — это тот факт, что для её вычисления не используетя линейное уравнение. Вместо него логистическая регерссионная модель строится на использовании сигмоиды (также называемой логистической функцией, т.к. она используется в логистической регрессии).
Для вас не обязательно досконально запоминать сигмоиду, чтобы преуспеть в МО. Но все-таки иметь некоторое представление об этой функции будет полезно.
Главная характеристика сигмоиды, которая стоит того, чтобы с ней разобраться — не важно какое значение вы передадите этой функции, она всегда вернет значение в промежутке 0-1.
Использование логистической регрессионной модели для предсказаний
Чтобы использовать логистическую регрессию для предсказаний, вам, как правило, нужно точно определить точку отсечения. Эта точка отсечения обычно 0.5.
Давайте использовать наш пример с диагностикой рака с предыдущего графика, чтобы увидеть этот принцип на практике. Если логистическая регрессионная модель выдаст значение ниже 0.5, то эта точка данных будет отнесена к категории доброкачественной опухоли. Подобным образом, если сигмоида выдаст значение выше 0.5, то опухоль отнесут к категории злокачественных.
Использование матрицы ошибок для измерения эффективности логистической регрессии
Матрица ошибок может быть использована в качестве инструмента для сравнения истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных показателей в МО.
Матрица ошибок, в частности, полезна, когда используется для измерения эффективности логистической регрессионной модели. Вот пример, как мы можем использовать матрицу ошибок:
В этой таблице TN означает «истинно отрицательно», FN — «ложно отрицательно», FP — «ложно положительно», TP — «истинно положительно».
Матрица ошибок полезна для оценки модели, есть ли в ней «слабые» квадранты в матрице ошибок. Как пример, она может иметь ненормально большое количество ложно положительных результатов.
Она также довольно полезна в некоторых случаях, для того чтобы убедиться, что ваша модель работает корректно в особенно опасной зоне матрицы ошибок.
В этом примере диагностики рака, например, вы бы хотели быть точно уверены, что у вашей модели не слишком большое количество ложно положительных результатов, т.к. это будет означать, что чью-то злокачественную опухоль вы диагностировали как доброкачественную.
Подведем итог
В этом разделе у вас было первое знакомство с моделью МО — логистической регрессией.
Вот краткое содержание того, что вы узнали о логистической регрессии:
Алгоритм k-ближайших соседей (K-Nearest Neighbors)
Алгоритм k-ближайших соседей может помочь решить задачу классификации, в случае, когда категорий больше, чем 2.
Что из себя представляет алгоритм k-ближайших соседей?
Это классификационный алгоритм, который базируется на простом принципе. На самом деле, принцип настолько прост, что лучше его продемонстрировать на примере.
Представьте, что у вас есть данные по высоте и весу футболистов и баскетболистов. Алгоритм k-ближайших соседей может быть использован для предсказания является ли новый игрок футболистом или баскетболистом. Чтобы это сделать, алгоритм определяет К точек данных, ближайших к объекту исследования.
Данное изображение демонстрирует этот принцип с параметром К = 3:
На этом изображении футболисты изображены голубыми отметками, а баскетболисты — оранжевыми. Точка, которую мы пытаемся классифицировать, покрашена в зеленый цвет. Так как большинство (2 из 3) ближайших к зеленой точке отметок окрашены в голубой (футбольные игроки), то значит алгоритм К-ближайших соседей предсказывает, что новый игрок тоже окажется футболистом.
Как построить алгоритм К-ближайших соседей
Основные шаги для построения данного алгоритма:
Важность переменной К в алгоритме К-ближайших соседей
Хотя это может быть не очевидно с самого начала, изменение значения К в данном алгоритме изменит категорию, в которую попадет новая точка данных.
Конкретнее, слишком маленькое значение К приведет к тому, что ваша модель будет точно прогнозировать на обучающем множестве данных, но будет крайне не эффективна для тестовых данных. Также, имея слишком высокий К показатель, вы сделаете модель неоправданно сложной.
Представленная ниже иллюстрация отлично показывает этот эффект:
Плюсы и минусы алгоритма К-ближайших соседей
Чтобы подвести итог знакомства с этим алгоритмом, давайте коротко обсудим достоинства и недостатки его использования.
Подведем итог
Краткое содержание того, что вы только что узнали о алгоритме К-ближайших соседей:
Дерево решений и Случайный лес (Decision Trees and Random Forests)
Дерево решений и случайный лес — это 2 примера древовидного метода. Точнее, деревья решений — это модели МО, используемые для прогнозирования через циклический просмотр каждой функции в наборе данных один за одним. Случайный лес — это ансамбль (комитет) деревьев решения, которые используют случайные порядки объектов в наборе данных.
Что такое древовидный метод?
Перед тем, как мы нырнем в теоретические основы древовидного метода в МО, будет нелишним начать с примера.
Представьте, что вы играете в баскетбол каждый понедельник. Более того, вы всегда приглашаете одного и того же друга пойти поиграть с вами. Иногда друг действительно приходит, иногда нет. Решение приходить или нет зависит от множества факторов: какая погода, температура, ветер и усталость. Вы начинаете замечать эти особенности и отслеживать их вместе с решением вашего друга играть или нет.
Вы можете использовать эти данные для предсказания придет ли ваш друг сегодня или нет. Одна из техник, которой вы можете воспользоваться — это дерево решений. Вот как это выглядит:
У каждого дерева решений есть 2 типа элементов:
Вот еще парочка определений, которые вы должны понимать перед тем, как мы начнем:
Как построить дерево решений с нуля
Построение дерева решений сложнее, чем может показаться. Это происходит потому что решение на какие разветвления (характеристики) делить ваши данные (что является темой из области энтропии и получения данных) — это математически сложная задача.
Чтобы ее разрешить, специалисты МО обычно используют множество деревьев решения, применяя случайные наборы характеристик, выбранных для разделения дерева на них. Другими словами, новые случайные наборы характеристик выбираются для каждого отдельного дерева, на каждом отдельном разделении. Эта техника называется случайные леса.
В общем случае, специалисты обычно выбирают размер случайного набора характеристик (обозначается m) так, чтобы он был квадратным корнем общего количества характеристик в наборе данных (обозначается р). Если коротко, то m — это квадратный корень из р и тогда конкретная характеристика случайным образом выбирается из m.
Выгоды использования случайного леса
Представьте, что вы работаете с множеством данных, у которого есть одна «сильная» характеристика. Иными словами, в этом множестве данных есть характеристика, которая намного более предсказуема в отношении конечного результата, чем остальные характеристики этого множества.
Если вы строите дерево решений вручную, то имеет смысл использовать эту характеристку для самого «верхнего» разделения в вашем дереве. Это значит, что у вас будет несколько деревьев, прогнозы которых сильно коррелируют.
Мы хотим этого избежать, т.к. использование средней от сильно коррелирующих переменных не снижает значительно дисперсию. Используя случайные наборы характеристик для каждого дерева в случайном лесу, мы декоррелируем деревья и дисперсия полученной модели уменьшается. Эта декорреляция — главное преимущество в использовании случайных лесов в сравнении с деревьями решений, построенными вручную.
Подведем итог
Итак, краткое содержание того, что вы только что узнали о деревьях решений и случайных лесах:
Метод опорных векторов(Support Vector Machines)
Метод опорных векторов это алгоритм классификации (хотя, технически говоря, они также могут быть использованы для решения регрессионных задач), который делит множество данных на категории в местах наибольших «разрывов» между категориями. Эта концепция станет более понятной, если разобрать следующий пример.
Что такое метод опорных векторов?
Метод опорных векторов (МОВ) — это модель МО с учителем, с соответствующими алгоритмами обучения, которые анализируют данные и распознают закономерности. МОВ может быть использован как для задач классификации, так и для регрессионного анализа. В этой статье мы посмотрим конкретно на использование метода опорных векторов для решения задач классификации.
Как МОВ работает?
Давайте капнем поглубже в то, как действительно работает МОВ.
Нам дан набор тренировочных примеров, какждый из которого промаркирован как принадлежащий к одной из 2х категорий, и с помощью этого набора МОВ строит модель. Эта модель распределяет новые примеры в одну из двух категорий. Это делает МОВ невероятностным двоичным линейным классификатором.
МОВ использует геометрию для составления прогнозов по категориям. Конкретнее модель метода опорных векторов сопоставляет точки данных как точки в пространстве и разделяет на отдельные категории так, что они разделяются настолько широким разрывом, насколько возможно. Прогноз принадлежности новых точек данных к определенной категории основывается на том, с какой стороны разрыва находится точка.
Вот пример визуализации, который поможет вам понять интуицию МОВ:
Как вы можете наблюдать, если новая точка данных падает на левую от зеленой линии сторону, то она будет отнесена к «красным», а если на правую — то к «синим». Эта зеленая линия называется гиперплоскостью, и является важным термином для работы с МОВ.
Давайте посмотрим следующее визуальное представление МОВ:
На этой диаграмме гиперплоскость обозначена как «оптимальная гиперплоскость» (optimal hyperplane). Теория метода опорных векторов дает такое определение оптимальной гиперплоскости — это гиперплоскость, которая максимизирует поле между двумя ближайшими точками данных из разных категорий.
Как вы видите, граница поля действительно затрагивает 3 точки данных — 2 из красной категории и 1 из синей. Эти точки, которые соприкасаются с границей поля, и называются опорными векторами — откуда и пошло название.
Подведем итог
Вот краткий очерк того, что вы только что узнали о методе опорных векторов:
Метод К-средних (K-Means Clustering)
Метод К-средних — это алгоритм машинного обучения без учителя. Это значит, что он принимает непомеченные данные и пытается сгруппировать кластеры подобных наблюдений ваших данных. Метод К-средних крайне полезен для решения реальных прикладных задач. Вот примеры нескольких задач, подходящих для этой модели:
Вот визуальное представление того, как это выглядит на практике:
Мы изучим математическую составляющую метода К-средних вследующем разделе этой статьи.
Как работает метод К-средних?
Первый шаг в работе метода К-средних — это выбор количества групп на которое вы хотите разделить ваши данные. Этим количеством и является значение К, отраженное в названии алгоритма. Выбор значения К в методе К-средних очень важен. Чуть позже мы обсудим как выбрать правильное значение К.
Далее, вы должны случайным образом выбрать точку в наборе данных и причислить ее к случайному кластеру. Это даст вам начальное положение данных, на котором вы прогоняете следующую итерацию до тех пор, пока кластеры перестанут изменяться:
Выбор подходящего значения К в методе К-средних
Строго говоря, выбор подходящего значения К — это довольно сложно. Не существует «правильного» ответа в выборе «лучшего» значения К. Один из методов, который специалисты по МО часто используют, называется «методом локтя».
Для использования этого метода, первое, что вам необходимо сделать, это вычислить сумму квадратов отклонений(sum of squared errors) — СКО для вашего алгоритма для группы значений К. СКО в методе К-средних определена как сумма квадратов расстояний между каждой точкой данных в кластере и центром тяжести этого кластера.
В качестве примера этого шага, вы можете вычислить СКО для значений К 2, 4, 6, 8 и 10. Далее вы захотите сгенерировать график СКО и этих значений К. Вы увидите, что отклонение уменьшается с увеличением значения К.
И это имеет смысл: чем больше категорий вы создадите на основе множества данных — тем более вероятно, что каждая точка данных окажется близко к центру кластера этой точки.
С учетом сказанного, основная идея метода локтя — это выбрать значение К при котором СКО резко замедлит темпы снижения. Это резкое снижение образует «локоть» на графике.
Как пример, вот график СКО относительно К. В этом случае, метод локтя предложит использовать значение К примерно равное 6.
Важно, что К=6 просто оценка приемлемого значения К. Не существует «лучшего» значения К в методе К-средних. Как и многие вещи в области МО, это очень зависящее от ситуации решение.
Подведем итог
Вот краткий очерк того, что вы только что узнали в этом разделе:
Метод главных компонент (Principal Component Analysis)
Метод главных компонент используется для преобразования набора данных c множеством параметров в новый набор данных с меньшим количеством параметров и каждый новый параметр этого набора данных — это линейная комбинация раннее существующих параметров. Эти преобразованные данные стремятся обосновать большую часть дисперсии оригинального набора данных с гораздо большей простотой.
Что такое метод главных компонентов?
Метод главных компонент (МГК) — это техника МО, которая используется для изучения взаимосвязей между наборами переменных. Другими словами, МГК изучает наборы переменных для того, чтобы определить базовую структуру этих переменных. МГК еще иногда называют факторным анализом.
На основании этого описания вы можете подумать, что МГК очень схож с линейной регрессией. Но это не так. На самом деле, эти 2 техники имеют несколько важных отличий.
Различия линейной регрессии и МГК
Линейная регрессия определяет линию наилучшего соответствия через набор данных. Метод главных компонентов определяет несколько ортогональных линий наилучшего соответствия для набора данных.
Если вы не знакомы с термином ортогональный, то это просто означает, что линии находятся под прямым углом друг к другу, как север, восток, юг и запад на карте.
Давайте рассмотрим пример, чтобы помочь вам понять это лучше.
Взгляните на метки осей на этом изображении. Главный компонент оси х объясняет 73% дисперсии в этом наборе данных. Главный компонент оси у объясняет около 23% дисперсии набора данных.
Это означает, что 4% дисперсии остается необъясненными. Вы можете уменьшить это число добавляя больше главных компонент в ваш анализ.
Подведем итог
Краткое содержание того, что вы только что узнали о методе главных компонент: