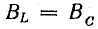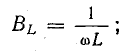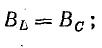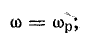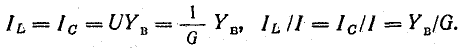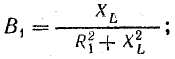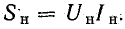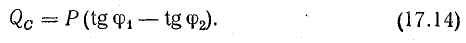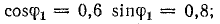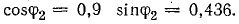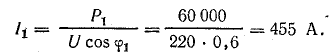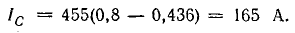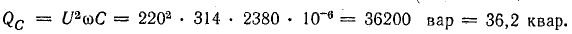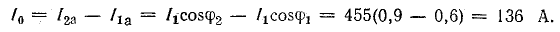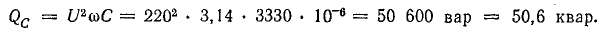Что такое резонанс токов

Особенности резонанса токов

Многие люди, изучая электронику и все, что с ней связано, сталкиваются с таким понятием как резонанс токов. Что оно собой представляет, при каких условиях возникает резонанс токов, как используется и как его правильно подсчитать? Об этом далее.

Что это такое

Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия

При каких условиях возникает

Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.

В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает

Как используется

Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.

Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.

Принцип действия

Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.

Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.

Как правильно рассчитать

Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.

Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.

Формула резонансных кривых

Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.

Расчет колебательного контура

Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.

В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.

Источник

Как возникает резонанс напряжения и токов: в чем опасность явления, как его можно использовать

Это явление можно наблюдать в индуктивных ёмкостных цепях. Резонанс широко используют в радиотехнике для наведения приёмника на определённую частоту.

У этого явления есть и отрицательная сторона – может повредить электрические приборы и кабели.

По сути, резонанс токов — это совмещение частоты разных систем. Давайте выясним, что это за явление, какова его значимость, в каких областях применяется.

Индуктивность, ёмкость и их реактивная сопротивляемость

Индуктивность – это свойство объекта копить энергию в намагниченном поле. Характеризуется тем, что фазный ток отстаёт от напряжения. Устройства индуктивности – это электрические моторы, трансформаторы.

Ёмкость – элементы, обладающие способностью копить энергию при помощи электрополя.

Характеризуются отставанием величины напряжения от величины тока. Это варикапы, различные конденсаторы. Это их главные свойства, детали в рамках данной статьи не учитываются.

Помимо названых элементов есть и другие, которые обладают определённой индуктивностью и ёмкостью.

Индуктивность и ёмкость в цепи тока переменной величины

Ёмкость в линии с током постоянной величины выглядит как разомкнутый отрезок цепи, индукция представлена проводником. При переменном токе реактивный резисторный аналог представлен катушками с устройствами конденсации.

Реактивная сопротивляемость зависима от значения ёмкости либо индуктивности, а также частоты тока с переменной величиной.

Глядя на расчёт реактивного значения, становится заметно, что имея определённые значения индуктивного либо ёмкостного элемента, разность их равняется нулю, и, как следствие, в остатке будет находиться активное сопротивление. У этой ситуации есть ещё некоторые нюансы.

Резонанс напряжения

Это явление возникнет, когда к генератору последовательно подключить катушку с конденсатором с одинаковыми реактивными сопротивлениями.

Обращаем ваше внимание, что ситуации, когда реактивными бывают только ёмкость и индуктивность, существуют только в идеале. А в реальности всегда есть сопротивление проводов, хотя и незначительное.

При резонансном эффекте конденсатор с дросселем обмениваются энергией. При запуске генератора, конденсатор начинает накапливать энергию, а затем, после выключения, в результате обмена начинают происходить колебания.

Схема, включающая в себя ёмкость и индуктивность, называется колебательным контуром.

Периодичность вычисляется формулой Томпсона:

Поскольку сопротивление зависимо от частоты, соответственно, при увеличении частоты сопротивляемость индуктивности возрастает, при этом у ёмкости, наоборот, снижается.

Общий показатель сопротивления будет ощутимо понижаться, когда сопротивления одинаковые.

К главным показателям контура относятся частота и передаточный коэффициент. Если разобрать контур с четырьмя полюсами, становится понятно, что передаточный коэффициент равен добротности (Q).

В резонансе, чем значительнейпоказатель добротности, тем значительней напряжение на контурных элементах по сравнению с напряжением на генераторе.

В контуре показатели мощности падают из-за сопротивления. Энергия поставщика используется лишь для поддержки колебаний.

Токовый резонанс

Это явление происходит при параллельном подключении ёмкости с индуктивностью.

Работает это по следующей схеме: ток большого значения проходит между катушкой и конденсаторным устройством, когда в части цепи без разветвления ток нулевой.

Это обуславливается возросшим сопротивлением при получении частоты резонанса. Проще говоря, в резонансной точке суммарное сопротивление достигает максимума. В результате роста или падения частоты одно сопротивление растёт, второе падает.

Обобщая, можно сказать, что всё происходит по аналогии с вышеупомянутым процессом, причины появления токового резонанса заключаются в следующем:

Практическое применение напряжения

Давайте разберём полезные и вредные свойства данного явления.

Несомненную пользу эффект резонанса напряжения принёс в радиоэлектронике. В цепи радиоприёмника вмонтирована катушка с конденсаторным устройством, соединённые с антенной.

Движением сердечника, меняя индукцию, либо ёмкостную величину с помощью конденсатора, подбирается частота резонанса. Вследствие этого напряжение катушки растёт, и радиоприёмник фиксирует определённую волну.

Но для кабелей такое явление довольно опасно, так как при подаче напряжения на кабель, не имеющий нагрузки, есть вероятность прострела изоляционной оболочки. Чтобы этого не произошло, подсоединяют балластную нагрузку.

Такая же ситуация ведёт к поломке частей электроники, приборов контроля и измерений и прочего электрического оборудования.

Резонансное явление напряжения – вещь достаточно интересная и заслуживает внимания. Резонанс возможен только в индуктивных ёмкостных цепях. В линиях, где активное сопротивление велико, это явление невозможно.

Подведём итог, коротко дав ответы по данной теме:

Ответ: в индуктивных ёмкостных схемах.

Ответ: реактивные сопротивления должны быть равны.

Ответ: Поменять частоту, добавить активное сопротивление.

Надеемся, теперь вам понятно, что это за явление, условия для его появления и практическое использование.

Источник

Что такое резонанс токов и напряжений

Простое объяснение явления резонанса токов и напряжений. Условия возникновения резонанса и его применение на практике.

Реактивные сопротивления индуктивности и емкости

Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.

Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.

Емкость и индуктивность в цепи переменного тока

Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.

Реактивное сопротивление катушки индуктивности определяется по формуле:

Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.

Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.

Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.

Резонанс напряжений

Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.

При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.

Напряжения на индуктивности и емкости примерно одинаковы, согласно закону Ома:

Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.

Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:

Период колебаний определяется по формуле Томпсона:

Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:

А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.

При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.

Коэффициент мощности будет равен:

Эта формула показывает, что потери происходят за счет активной мощности:

Резонанс токов

Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:

Применение на практике

Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления.

Заключение

Резонанс напряжений и токов — интересное явление, о котором нужно знать. Он наблюдается только в индуктивно-емкостных цепях. В цепях с большим активным сопротивлениям он не может возникнуть. Подведем итоги, кратко ответив на основные вопросы по этой теме:

В индуктивно-емкостных цепях.

Возникает при условии равенства реактивных сопротивлений. В цепи должно быть минимальное активное сопротивление, а частота источника питания совпадать с резонансной частотой контура.

В обоих случаях по формуле: w=(1/LC)^(1/2)

Увеличив активное сопротивление в цепи или изменив частоту.

Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео по теме:

Источник

Резонанс токов

Содержание:

Резонанс токов:

При рассмотрении параллельного соединения катушки и конденсатора был отмечен случай равенства активной и реактивной проводимостей

Условия возникновения резонанса

Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ω_р, а

Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.

Сначала рассмотрим этот режим для схемы идеализированной цепи (рис. 17.6, а). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.

Рис. 17.6. К вопросу о резонансе токов

Реактивные проводимости зависят от частоты вынужденных колебаний. Для рассматриваемой схемы:
активная проводимость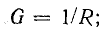

реактивные проводимости

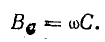
При резонансе токов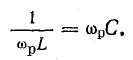

Отсюда определяют резонансную частоту: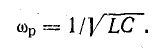

Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений [см. формулу (17.8)] и для частоты собственных колебаний в контуре без потерь.
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.

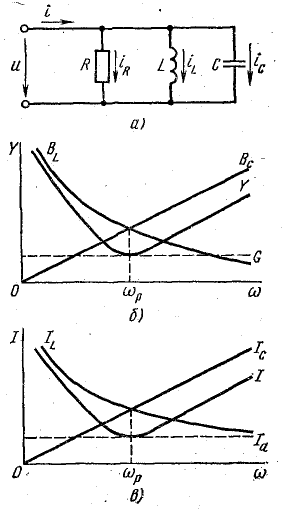
Резонансные кривые

На рис. 17.6, б показаны зависимости проводимостей от частоты. Полная проводимость цепи Y при резонансной частоте ω_р оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.

При заданном напряжении источника энергии ток в цепи пропорционален проводимости (рис. 17.6, в): 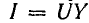, поэтому кривая I(ω) по форме повторяет кривую Y(ω). Состояние резонанса токов характеризуется наименьшей величиной тока в цепи и равенством нулю угла сдвига фаз между напряжением и током (φ_р = 0).

При резонансе токов отношение тока индуктивного или емкостного к току в неразветвленной части цепи равно отношению волновой проводимости 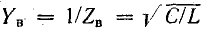к активной проводимости цепи G.
Реактивные проводимости при резонансе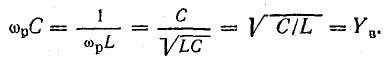

Поэтому

Добротность контура

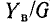
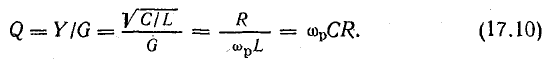
При параллельном соединении элементов качество резонансной цепи считается тем выше, чем больше отношение , которое и в этом случае называется добротностью:

Чем меньше потери энергии в цепи (этому соответствует большая величина R), тем больше добротность.

Параметры реальных катушек и конденсаторов (R, L, С) измеряются и задаются в справочниках применительно к их схемам замещения с последовательным соединением активных и реактивных элементов (см. рис. 14.11, б).
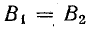
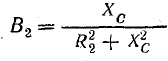
Условие резонанса токов — равенство реактивных проводимостей обеих ветвей — остается справедливым, и в этом случае
,
где R₁ и R₂ — активные сопротивления катушки и конденсатора с потерями.
Приравнивая реактивные проводимости, получим исходное уравнение для определения резонансной частоты

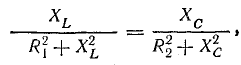
или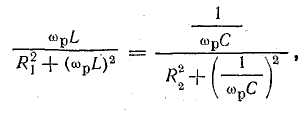

откуда

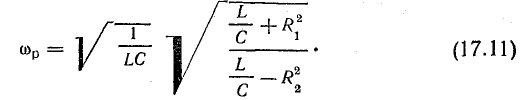
Из «того выражения видно, что резонансная частота зависит от активных сопротивлений катушки и конденсатора. Если потери энергии в катушке и конденсаторе малы (R₁ и R₂ малы) и ими можно пренебречь, для резонансной частоты получается выражение, найденное раньше для идеализированной цепи.

Компенсация реактивной мощности в электрических сетях с помощью конденсаторов

Было отмечено, что в электрической цепи переменного тока, в которой имеются катушка индуктивности и конденсатор, включенные последовательно или параллельно, общая реактивная мощность цепи всегда меньше, чем реактивная мощность каждого из элементов.

Благодаря взаимному обмену энергией между катушкой и конденсатором и рис. 14.5 источник частично или полностью освобождается от поставки реактивной энергии в цепь.

В этом случае говорят о компенсации реактивной мощности катушки реактивной мощностью конденсатора и наоборот (реактивные мощности Q_L и Q_С имеют противоположные знаки). Полная компенсация реактивной мощности имеет место при резонансе.

Компенсация реактивной мощности в электрических сетях имеет большое технико-экономическое значение. Далее кратко рассмотрены общие сведения по этому вопросу и принцип применения конденсаторов для компенсации реактивной мощности.

Реактивная мощность электрических установок

Энергетический процесс в катушке индуктивности, включенной в цепь переменного тока, характеризуется активной мощностью и реактивной мощностью .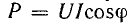

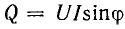
В электрической схеме замещения такая катушка представлена активным сопротивлением R и индуктивностью L, или активной проводимостью G и реактивной проводимостью Y.

В этом отношении катушке индуктивности подобны многочисленные устройства переменного тока: асинхронные двигатели, индукционные нагревательные установки, трансформаторы, воздушные линии и др.
Получая от генераторов электрическую энергию, эти устройства передают или преобразуют ее в другие виды энергии (активная мощность Р), т. е. выполняют те функции, для которых созданы.

Одновременно они обмениваются энергией с источниками (реактивная мощность Q), что является процессом хотя и нежелательным, но неизбежным, так как без магнитного поля и периодического накопления энергии в нем перечисленные устройства работать не могут.

Если реактивная мощность устройства не равна нулю, то отношение 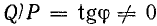, а коэффициент мощности .

На каждом предприятии одновременно работают электродвигатели (их может быть десятки и сотни), трансформаторы и другие устройства. Чем больше их число и чем меньше их коэффициент мощности, тем больше общая реактивная мощность электрооборудования производственного участка, цеха, всего предприятия.

Величина общей реактивной мощности электрической установки или электрооборудования предприятия в целом зависит еще и от правильного выбора, степени загрузки электродвигателей, трансформаторов, от соблюдения правил эксплуатации электрооборудования.

Далее будет показано, что за счет реактивной мощности потребителей электрический ток в сетях оказывается больше, чем требуется по величине активной нагрузки. С этим связана одна из проблем проектирования и эксплуатации электрических сетей. При передаче электрической энергии, особенно на большие расстояния, из-за наличия индуктивных и емкостных сопротивлений в элементах сети переменного тока возникает также проблема поддержания заданного уровня напряжения на всех приемниках.
Для обеспечения оптимальной величины тока и требуемых величин напряжения в сети необходимо иметь оптимальный баланс реактивных мощностей (индуктивной и емкостной).

Влияние величины реактивной мощности на технико-экономические показатели электроустановок

Для выяснения влияния величины реактивной мощности на экономические показатели электротехнических установок рассмотрим приемник энергии (например, асинхронный электродвигатель), работающий с постоянной активной мощностью при постоянном напряжении в сети.
Ток в приемнике, а следовательно, и в проводах, соединяющих его с источником энергии, при этих условиях зависит от величины реактивной мощности Q: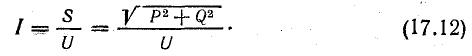

Чем больше реактивная мощность приемника, тем больший ток должен быть в самом приемнике, в генераторе, соединительных проводах, трансформаторе и других элементах сети электроснабжения.
Мощность тепловых потерь, согласно закону Ленца — Джоуля, пропорциональна квадрату тока и сопротивлению проводов: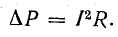

Очевидно, чем больше ток приемника, тем больше потери энергии во всех элементах электрической цепи.

Стоимость потерянной энергии входит в эксплуатационные расходы. Уменьшение реактивной мощности приемников ведет к уменьшению их токов, сокращению потерь энергии и эксплуатационных расходов.
Если электрическая установка спроектирована с относительно большей величиной реактивной мощности, то оборудование (коммутационная аппаратура, приборы контроля и т. д.) и провода необходимо выбрать на большие токи, чем при меньшей величине реактивной мощности.
Это значит, что оборудование должно быть установлено относительно больших размеров, а провода — большего сечения. Последнее повлечет за собой увеличение объема зданий, утяжеление фундаментов и опор и т. п.
Уменьшение реактивной мощности приемников энергии сокращает капитальные затраты.

Генераторы электрической энергии и трансформаторы характеризуются номинальной мощностью — произведением номинальных величин напряжения и тока:

Наиболее полное использование генераторов и трансформаторов соответствует режиму работы с номинальным током при номинальном напряжении (особые случаи, когда допускается некоторая перегрузка оборудования при эксплуатации, здесь не учитываются).

Величина активной мощности генератора равна активной мощности питающихся от него приемников.

Компенсация реактивной мощности

Из приведенных рассуждений следует, что реактивную мощность установок, потребляющих электрическую энергию, надо по возможности сокращать.
На практике это достигается путем правильного выбора мощности электродвигателей переменного токаи трансформаторов, рациональной эксплуатации их без недогрузки и работы вхолостую. Эти и некоторые другие меры уменьшения реактивной мощности, связанные с выбором и эксплуатацией электрооборудования, называют естественными.

В тех случаях, когда естественные меры не могут обеспечить оптимальной величины реактивной мощности установки, принимают искусственные меры для ее компенсации.

Одной из таких мер является включение параллельно к приемникам батареи конденсаторов.

Для определения мощности и емкости батареи конденсаторов должны быть известны величины напряжения сети U, реактивной мощности установки до компенсации (Q₁) и после компенсации (Q₂).

Можно установить батарею конденсаторов мощностью Q_C = Q₁, тогда Q₂ = 0. Полная компенсация реактивной мощности освобождает полностью сеть от реактивного тока.

Однако технико-экономические расчеты показывают, что полная компенсация в большинстве случаев не является оптимальным решением вопроса, так как компенсационное устройство оказывается более сложным и дорогим, чем при некоторой оптимальной величине реактивной мощности Q₂, которую определяют на основе технико-экономического сопоставления вариантов (Определение оптимальной величины Q₂, выбор вида компенсирующего устройства и места его установки в сети рассматриваются в специальных курсах).

Мощность батареи конденсаторов

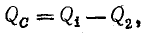
а емкость


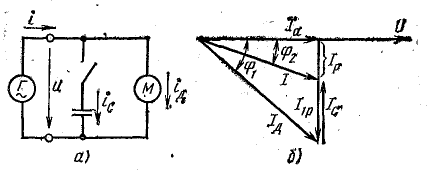
Рис. 17.7. К вопросу о компенсации реактивной мощности

Сущность компенсации реактивной мощности с помощью конденсаторов видна из векторной диаграммы (рис. 17.7, б), построенной для схемы (рис. 17.7, а), на которой параллельно приемнику, например асинхронному двигателю (группе двигателей), может быть включена конденсаторная батарея. До включения конденсаторов ток в подводящих проводах I_д отстает по фазе от напряжения на угол φ₁. После включения батареи реактивная составляющая I_1р тока двигателя частично компенсируется емкостным током I_C, в связи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз — до φ₂ (в обменном энергетическом процессе между генератором и приемником участвует меньшее количество электромагнитной энергии).

Активная составляющая тока в проводах не изменяется, следовательно, по активной мощности режим цепи остается прежним: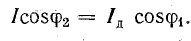

Ток батареи конденсаторов имеет величину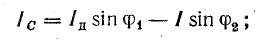


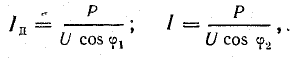
где Р — активная мощность приемника (в данном случае двигателя);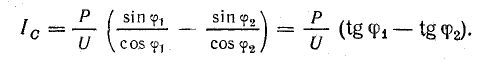

Емкость батареи конденсаторов

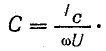
Мощность батареи конденсаторов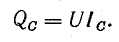

Нетрудно заметить, что мощность конденсаторов можно найти, не подсчитывая тока I_C:

Задача 17.7.

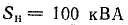
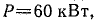
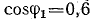
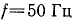
К трансформатору номинальной мощностью и номинальным напряжением 220 В подключена группа электродвигателей, общая активная мощность которых при частоте (рис. 17.8, а). Если параллельно группе двигателей включить батарею конденсаторов, реактивная мощность установки (двигатели — батарея конденсаторов) уменьшится и соответственно уменьшится нагрузка трансформатора.
Определить емкость и мощность батареи конденсаторов и дополнительную осветительную нагрузку, которые нужно подключить к трансформатору так, чтобы реактивная мощность установки уменьшилась до величины, при которой коэффициент мощности 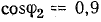при полной загрузке трансформатора.
Определить емкость и мощность батареи конденсаторов в том случае, когда 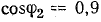при отсутствии дополнительной осветительной нагрузки.
Решение. 1. В первоначальном режиме трансформатор был загружен до номинальной мощности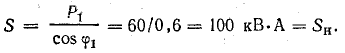

Дополнительную осветительную нагрузку можно присоединить только за счет разгрузки трансформатора от части реактивной мощности путем включения батареи конденсаторов.
Согласно условию задачи, трансформатор после компенсации части реактивной мощности остается полностью загруженным, следовательно, при неизменном напряжении ток трансформатора должен остаться прежним: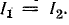

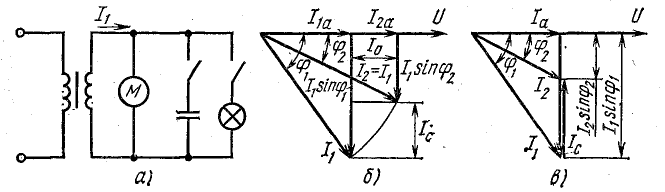
Рис. 17.8. К задаче 17.7

Из векторной диаграммы (рис. 17.8, б) следует выражение для тока конденсатора: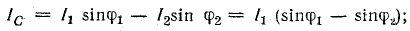

при

при

Ток установки до компенсации реактивной мощности

Ток батареи конденсаторов

Емкость батареи конденсаторов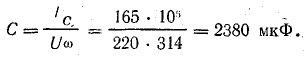

Мощность батареи конденсаторов

Активный ток дополнительной осветительной нагрузки

Мощность осветительной нагрузки

2. При отсутствии дополнительной осветительной нагрузки необходимый ток в батарее конденсаторов (рис. 17.8, в)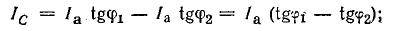


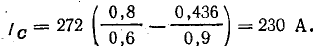
Емкость батареи конденсаторов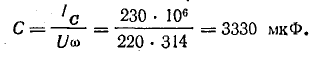

Мощность батареи конденсаторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник