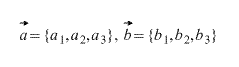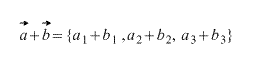Что такое результирующий вектор

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

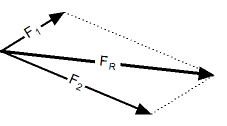
Процедура сложения векторов по правилу параллелограмма заключается в следующем:

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:

Тригонометрический способ. Сложение векторов тригонометрическим способом.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Источник

Результирующий вектор: расчет, примеры, упражнения

Содержание:

Таким образом получаются такие векторы, как результирующая скорость, ускорение или сила. Например, когда на тело действует несколько сил. F₁, F₂, F₃,…. векторная сумма всех этих сил равна чистой силе (равнодействующей), которая математически выражается следующим образом:

F₁ + F₂ + F₃ +… = F_р или F_N

Результирующий вектор, будь то силы или любая другая величина вектора, находится с применением правил сложения векторов. Поскольку векторы имеют направление и смысл, а также числовое значение, недостаточно добавить модули, чтобы получить результирующий вектор.

Это верно только в том случае, если задействованные векторы направлены в одном направлении (см. Примеры). В противном случае необходимо использовать методы векторной суммы, которые в зависимости от случая могут быть геометрическими или аналитическими.

Примеры

Геометрическими методами нахождения результирующего вектора являются метод траверса и метод параллелограмма.

Что касается аналитических методов, существует метод компонентов, с помощью которого можно найти вектор, полученный из любой системы векторов, при условии, что у нас есть его декартовы компоненты.

Геометрические методы сложения двух векторов

Предположим, что векторы или Y v (Мы обозначили их жирным шрифтом, чтобы отличить их от скаляров). На рисунке 2а) они расположены на плоскости. На рисунке 2 б) он переведен в вектор v таким образом, что его начало совпадает с концом или. Результирующий вектор идет от начала координат первого (или) до кончика последнего (v):

Обратите внимание, что порядок, в котором выполняется эта процедура, не имеет значения, поскольку сумма векторов коммутативна.

Метод параллелограмма

Этот метод очень подходит, когда вам нужно добавить два вектора, исходные точки которых совпадают, скажем, с началом системы координат x-y. Предположим, что это так для наших векторов или Y v (рисунок 3а):

На рисунке 3b) параллелограмм построен с помощью пунктирных линий, параллельных или уже v. Результирующий вектор имеет начало в точке O и конец в точке пересечения пунктирных линий. Эта процедура полностью эквивалентна описанной в предыдущем разделе.

Упражнения

-Упражнение 1

Учитывая следующие векторы, найдите результирующий вектор с помощью метода обхода.

Решение

Полученная фигура представляет собой многоугольник, а результирующий вектор (синий) называется р. Если вы начнете с другого вектора, сформированная форма может быть другой, как показано в примере, но результирующий вектор будет таким же.

Упражнение 2.

На следующем рисунке известно, что модули векторов или Y v соответственно они равны u = 3 условных единицы и v = 1,8 условных единиц. Угол, который или форма с положительной осью абсцисс составляет 45º, а v образует 60º с осью Y, как показано на рисунке. Найдите результирующий вектор, величину и направление.

Решение

В предыдущем разделе результирующий вектор был найден методом параллелограмма (на рисунке выделен бирюзовым цветом).

или_Икс = u. cos 45º = 3 x cos 45º = 2,12; или_Y = u. грех 45º = 3x грех 45º = 2,12

Вычисление декартовых компонент результирующего вектора

Результирующий вектор находится путем алгебраического сложения соответствующих компонентов x и y, чтобы получить их декартовы компоненты:

р_Икс = 2.12 + 1.56 = 3.68

Как только декартовы компоненты указаны, вектор становится полностью известным. Полученный вектор можно записать в квадратных скобках (подтяжки):

R = условные единицы

р = 3.68 я + 1.22 j условные единицы

Поскольку обе компоненты результирующего вектора положительны, вектор р принадлежит к первому квадранту, который ранее уже был замечен графически.

Величина и направление результирующего вектора

Зная декартовы компоненты, величина R вычисляется по теореме Пифагора, так как полученный вектор рвместе со своими компонентами R_Икс и R_Y образуют прямоугольный треугольник:

Величина или модуль: R = (3.68 2 + 1.22 2 ) ½ = 3.88

Направление q, взяв за основу положительную ось x: q = arctan (R_Y / Р_Икс) = arctg (1,22 / 3,68) = 18,3 º

Ссылки

Что такое стереотипы? 4 способа, которыми они влияют на нас

Источник

Векторы

Никто не будет спорить, что к месту назначения невозможно добраться не зная направления движения. В физике это понятие называется вектором. До этого момента мы с вами оперировали некоторыми числами и значениями, которые называются величинами. Вектор отличается от величины наличием направления.

При работе с вектором оперируют его направлением и величиной. Физический параметр без учета направления называют скаляром.

В физике для обозначения векторов используют заглавную букву со стрелкой наверху.

Векторы можно сравнивать. Два вектора будут равны, если они имеют одинаковую величину и направление.

1. Сложение векторов

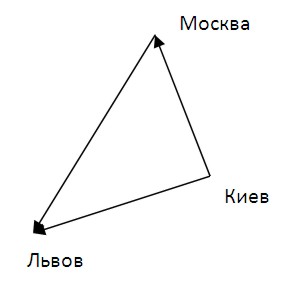
Вектора можно складывать. Результирующий вектор является суммой обоих векторов и определяет расстояние и направление. Например, вы проживаете в Киеве и решили проведать старых друзей в Москве, а оттуда сделать визит к любимой теще во Львов. Насколько далеко вы будете находиться от родного дома, гостюя у мамы жены?

Для ответа на этот вопрос вам надо начертить вектор от исходной точки путешествия (Киев) и до конечной (Львов). Новый вектор определяют результат всего путешествия от начала и до конца.

2. Вычитание векторов

Вектора можно не только складывать, но и вычитать! Для этого надо совместить основания вычитаемого и вычитающего векторов и соединить их концы со стрелками:

3. Векторы и числа

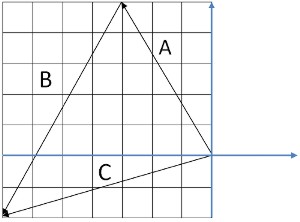
Наложим на наши вектора координатную сетку. Для вектора А можно сказать, что он направлен на 5 клеток вверх (положительное значение оси Y) и на 3 клетки влево (отрицательное значение оси Х): X=-3; Y=5.

Для вектора В: направление на 4 клетки влево и 7 клеток вниз: X=-4; Y=-7.

Т.о., для сложения векторов по осям X и Y надо сложить их координаты. Чтобы получить координаты результирующего вектора по осям X и Y:

4. Разбиение векторов на координаты

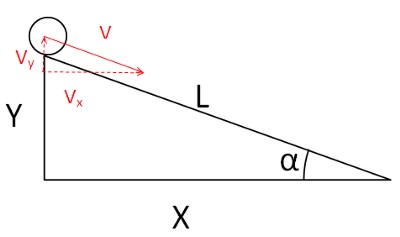
Рассмотрим задачу: шар движется со скоростью 10м/с по наклонной плоскости с длиной основания X=1м, распложенной под 30° к горизонту. Требуется определить время, за которое шар переместится от начала к концу плоскости.

В данной задаче скорость является вектором V с величиной 10м/с и направлением α=30° к горизонтали. Чтобы определить скорость перемещения шара вдоль основания наклонной плоскости, нам надо определить X-составляющую перемещения шара, которая является скаляром (имеет только значение, но не направление) и обозначается V_x. Аналогично, Y-составляющая скорости также скаляр и обозначается V_y. Вектор скорости через составляющие: V = (V_x;V_y)

Определим составляющие (V_x;V_y). Вспоминаем тригонометрию:

Х-составляющая скорости шара:

V_x = V·cosα = V·cos30° = 10,0·0,866 = 8,66 м/с

Горизонтальная скорость шара равна 8,66 м/с.

Т.к. длина основания наклонной плоскости равна 1м, то это расстояние шар преодолеет за:

1,00(м)/8,66(м/с) = 0,12 с

Т.о., шару потребуется 0,12с для перемещения вдоль наклонной плоскости. Ответ: 0,12с

Интереса ради определим Y-составляющую скорости:

V_y = V·sinα = 10·1/2 = 5,0 м/с

Поскольку время «путешествия» шара одинаково для обеих составляющих, то можем определить высоту Y, с которой катился шар:

5,0(м/с)·0,12(с) = 0,6 м

Расстояние, пройденное шаром:

L = √1,00 2 + 0,60 2 = √1,36 = 1,16м

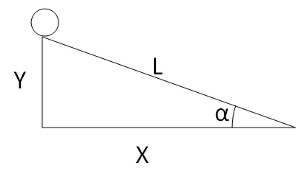
Обратная задача

Рассмотрим задачу, обратную предыдущей:

Шар переместился вдоль наклонной плоскости на высоту 0,6м, при этом в горизонтальной плоскости его перемещение составило 1,0м. Необходимо найти расстояние, пройденное шаром и угол.

Расстояние вычисляем по теореме Пифагора:

L = √1,00 2 + 0,60 2 = √1,36 = 1,16м

X = L·cosα; Y = L·sinα

X/L = cosα; Y/L = sinα

Теперь можно найти угол:

α = arccos(X/L); α = arcsin(Y/L)

α = arccos(1/1,16) = 30°

Промежуточное вычисление L можно исключить:

Y = X·tgα

α = arctg(Y/X)

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

Что такое результирующий вектор

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник