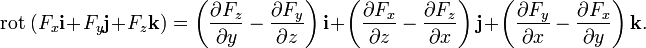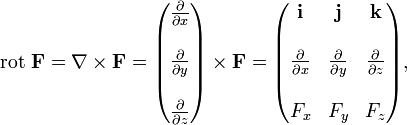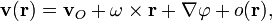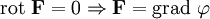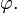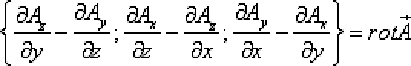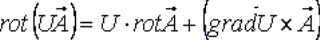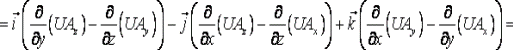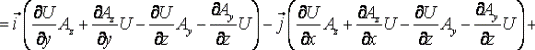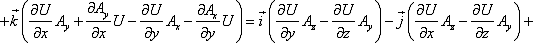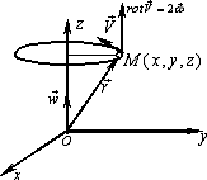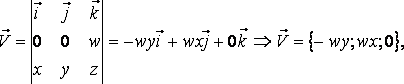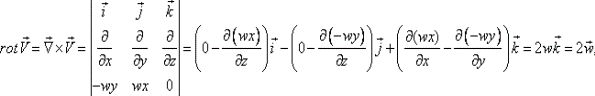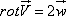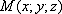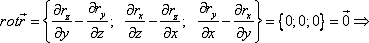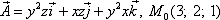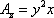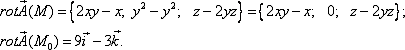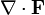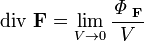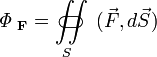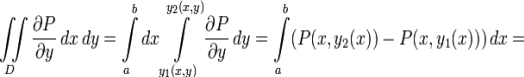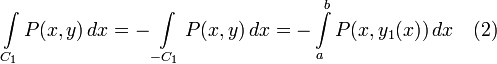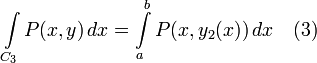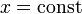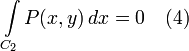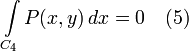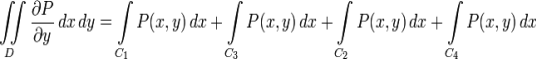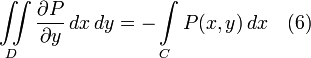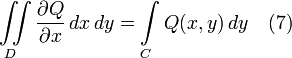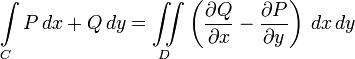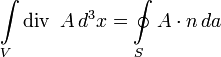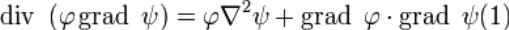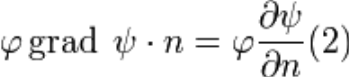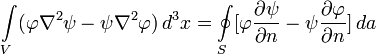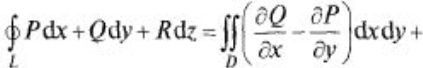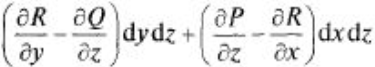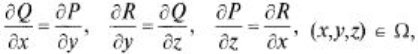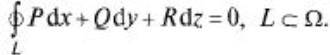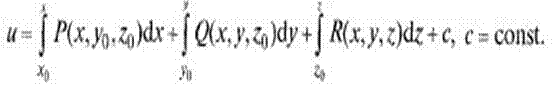Что такое ротор в физике

Ротор векторного поля

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также 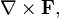где — векторный дифференциальный оператор набла.

Содержание

Математическое определение

Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

.

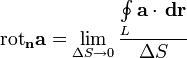
Нормаль 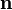к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.

В трёхмерной декартовой системе координат 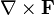вычисляется следующим образом:

Для удобства запоминания можно условно представлять ротор как векторное произведение:

где i, j и k — единичные орты для осей x, y и z соответственно.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).

Физическая интерпретация

По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением

где 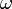— вектор углового вращения элемента среды в точке О, а — квадратичная форма от координат — потенциал деформации элемента среды.

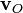
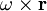
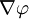
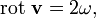
Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор ), вращательного движения (вектор ) и потенциального движения — деформации (вектор ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.

Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).

Основные свойства

Следующие свойства могут быть получены из обычных правил дифференцирования.

для любых векторных полей F и G и для всех вещественных чисел a и b.

При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:

Верно и обратное: если поле безвихревое, то оно потенциально:

для некоторого скалярного поля

Источник

Ротор

Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot или :

, где

векторный дифференциальный оператор набла, и F изучаемое векторное поле. В декартовой системе координат

вычисляется следующим образом:

Для простоты восприятия можно представлять ротор как

Или как детерминант следующей матрицы:

где i, j и k — единичные векторы для осей x, y и z соответственно.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).

Физическая интерпретация

Основные свойства

Следующие свойства могут быть получены из обычных правил дифференцирования.

для любых векторных полей F и G и для всех действительных чисел a и b.

Источник

Ротор и его основные свойства

Определение ротора векторного поля:

Ротором или вихрем векторного поля 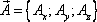называется вектор с проекциями

Основные свойства ротора:

— это векторная величина, которая является дифференциальной (т.е. точечной) характеристикой векторного поля .

— свойство линейности.

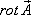
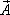
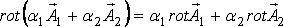
Ротор произведения скалярной и векторной ункции вычисляется по формуле:

Физический смысл ротора

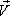
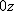
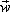
Некоторое физическое истолкование понятия ротора можно получить, если рассматривать векторное поле линейных скоростей твердого тела (материальной точки M), вращающегося вокруг оси с постоянной угловой скоростью .

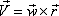
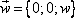
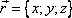
Из физики известно, что , где — это угловая скорость вращения, — это радиус вектор точки М.

то есть поле линейных скоростей тела, вращающегося вокруг неподвижной оси есть плоское векторное поле.

Вычислим его ротор равен:

то есть

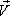
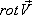
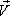
Следовательно, ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения. Таким образом, характеризует вращательную способность поля , наличие у этого поля “закрученных” векторных линий или “вихрей”.

В технической литературе ротор векторного поля часто называют вихрем этого поля.

Примеры 2 (вычисление ротора векторного поля)

Вычислить ротор радиус-вектора 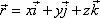точки

Составляем формулу (4) для и делаем вычисления:

, ,

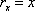
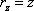
векторное поле 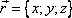не обладает вращательной способностью.

Вычислить 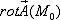, если

Записываем проекции данного векторного поля:

,

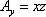
и по формуле (4) получаем, что

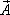
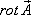
Из рассмотренного примера следует, что любое векторное поле сопровождается другим векторным полем его ротора.

Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учетом знака. Поэтому можно дать более короткое определение дивергенции:

Оператор дивергенции, применённый к полю, обозначают как

F или

Определение дивергенции выглядит так:

где — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объема ее внутренности).

В обоих случаях подразумевается, что:

Это определение не привязано к определённым координатам, например к декартовым, что может представлять дополнительное удобство в определённых случаях.

На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая C замкнута.

Доказательство:

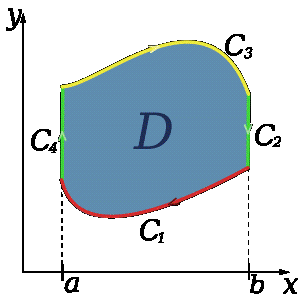
Для кривой C, ограничивающей область D зададим направление обхода по часовой стрелке. Тогда

Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:

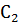
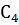
Криволинейные интегралы по и будут равны нулю, так как

Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:

Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой C в отрицательном направлении:

Аналогично доказывается формула:

если в качестве области D взять область, правильную в направлении OX.

Складывая (6) и (7), получим:

Если бы в электростатических задачах мы всегда имели дело с дискретным или непрерывным распределением заряда без всяких граничных поверхностей, то общее решение для скалярного потенциала

было бы самой удобной и непосредственной формой решения таких задач и не нужны были бы ни уравнение Лапласа, ни уравнение Пуассона. Однако в действительности в целом ряде, если не в большинстве, задач электростатики мы имеем дело с конечными областями пространства (содержащими или не содержащими заряд), на граничных поверхностях которых заданы определенные граничные («краевые») условия.

Эти граничные условия могут быть заменены некоторым соответственно подобранным распределением зарядов вне рассматриваемой области (в частности, в бесконечности), однако приведенное выше соотношение в этом случае уже непригодно для расчета потенциала, за исключением некоторых частных случаев (например, в методе изображений).

Для рассмотрения задач с граничными условиями необходимо расширить используемый нами математический аппарат, а именно вывести так называемые формулы, или теоремы Грина (1824 г.). Они получаются непосредственно из теоремы о дивергенции

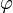
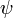
которая справедлива для любого векторного поля А, определенного в объёме V, ограниченном замкнутой поверхностью S. Пусть где и — произвольные дважды непрерывнодифференцируемые скалярные функции.

Где нормальная производная на поверхности S (по направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина

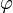
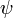
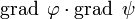
Напишем такую же формулу, поменяв в ней местами и и вычтем её из (3). Тогда члены с произведением обратятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина:

В физике и математике теорема Грина дает соотношение между линейным интегралом простой ограниченной кривой С и двойным интегралом по плоской поверхности D ограниченной кривой С. И в общем виде записывается следующим образом.

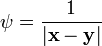
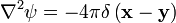
Третье уравнение Грина получается из второго уравнения путем замены и замечания о том, что

в R ³.

Если дважды дифференцируема на U.

если x ∈ Int U, если x ∈ ∂U и плоскость касания только в x.

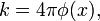
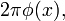
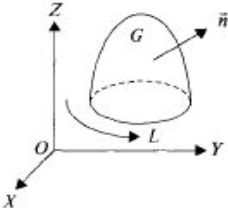
Формула Стокса устанавливает связь между поверхностным и криволинейным интегралами, а также обобщает формулу Грина а пространственный случай. Т: Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными на гладкой ориентированной поверхности G, ограниченной гладкой замкнутой кривой L. Тогда

Эта формула называется формулой Стокса.

Если сторона поверхности выбрана, то направление обхода контура L берется положительным, т.е. таким, что при обходе контура по выбранной стороне поверхности:

Из формулы Стокса следует, что если

то криволинейный интеграл по любой пространственной замкнутой кривой L равен нулю:

u(x,y,z): Pdx + Qdy + Rdz = du,

Заключение

Для того что бы сделать вывод о проделанной работе обратимся к задачам, которые были поставлены в введении.

Итак, примерами векторных полей служат силовое поле (поле тяготения, электрическое и электромагнитное поля) и поле скоростей текущей жидкости. Векторное поле задано, если в каждой точке Р поля указан соответствующий этой точке вектор А(Р).

Дивергенцией, или расходимостью, векторного поля А(Р) в точке Р называется предел отношения потока вектора через поверхность, окружающую точку Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку Р.

Циркуляцией вектора А(Р) вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора А(Р) на вектор dS касательной к контуру.

Литература

1. М.А. Красносельский, А.И. Перов, А.И. Поволоцкий, П.П. Зайбеко, «Векторные поля на плоскости» М.,Государственное издательство физико-математической литературы 1963 г.

2. Мышкис «Лекции по высшей математике».

3. Данко П.Е., Попов А.Г., Кожевников Т.Я., «Высшая математика в упражнениях и задачах» М., Выс.школа 1980 г.

4. Красносельский М.А. «Топологические методы в теории нелинейных интегральных уравнений.», М.: Гостехиздат, 1956 г.

Источник