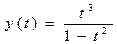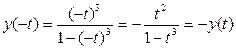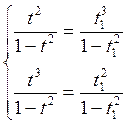Что такое самопересечение в математике
Самопересечения точка
Смотреть что такое «Самопересечения точка» в других словарях:
САМОПЕРЕСЕЧЕНИЯ ТОЧКА — одна из особых точек кривой или поверхности. См., напр., Двойная точка … Математическая энциклопедия
Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия
Точка — I Точка (математическая) одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых… … Большая советская энциклопедия
Узловая точка — самопересечения точка, Особая точка кривой … Большая советская энциклопедия
УЗЛОВАЯ ТОЧКА — точка самопересечения кривой. При параметрич. задании кривой У. т. соответствует двум или более значениям параметра. Например, у кривой а sinЗj У. т. начало координат … Математическая энциклопедия
ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия
Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия
Особая точка — указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия
Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия
ДВОЙНАЯ ТОЧКА — один из видов особых точек кривой F(x, y) = 0, в к рой первые частные производные равны нулю и по крайней мере одна из вторых частных производных функции F(х, у)не равна нулю. При исследовании строения кривой вблизи Д. т. рассматривают знак… … Математическая энциклопедия
самопересечение
Смотреть что такое «самопересечение» в других словарях:
самопересечение — самопересечение … Орфографический словарь-справочник
самопересечение — сущ., кол во синонимов: 1 • пересечение (10) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
самопересечение — самопересеч ение, я … Русский орфографический словарь
самопересечение — самопересече/ние, я … Слитно. Раздельно. Через дефис.
двусвязная форма — 3.5.1 двусвязная форма (2 manifold): Форма, в любой точке на границе которой можно создать достаточно маленькую сферу так, чтобы внутренняя часть этой сферы делилась данной границей точно на две части. Как правило, границу образуют ребра и грани … Словарь-справочник терминов нормативно-технической документации
КРИСТАЛЛОАКУСТИКА — изучает особенности распространения акустич. волн в кристаллах, а также влияние анизотропии физ. св в кристаллов па хар ки акустич. волн (особенности их поляризации, поглощения и отражения, дифракции и др.). Анизотропия фазовых скоростей… … Физическая энциклопедия
АСИММЕТРИЧНОЕ МНОГООБРАЗИЕ — ориентируемое многообразие М, для к рого не существует гомеоморфизма, обращающего ориентацию. Напр., комплексная проективная плоскость есть А. м., так как самопересечение комплексной прямой равно +1 или 1 в зависимости от ориентации. Отличие нек… … Математическая энциклопедия
НОРМАЛЬНЫЙ ПУЧОК — аналог нормального расслоения в теории пучков. Пусть морфизм окольцованных пространств такой, что гомоморфизм сюръективен, и пусть Тогда есть пучок идеалов в и поэтому является модулем. Пучок … Математическая энциклопедия
УРОВНЯ ЛИНИЯ — функции Грина множество точек где G(z, z0) функция Грина области Dкомплексной плоскости с полюсом в точке Если область Dодносвязна, то структура этого множества легко выясняется при конформном отображении Dна круг переводящем точку z0 в Функция… … Математическая энциклопедия
Лист Мёбиуса — Лента Мёбиуса Лист Мёбиуса (лента Мёбиуса, петля Мёбиуса) топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство R³. Попасть из одной … Википедия
Бутылка Клейна — Бутылка Клейна, погружённая в трёхмерное пространство. Бутылка Клейна это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в … Википедия
Замкнутые самопересекающиеся ломаные
Александр Блинков, Александр Грибалко
«Квантик» №11, 2019
В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).
Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).
И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).
Нас будут интересовать замкнутые самопересекающиеся ломаные.
Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).
Задача 1
Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно два раза?
Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.
Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.
Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.
Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.
Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.
Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.
Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).
Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.
Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?
Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.
Задача 2
Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно один раз?
Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.
Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).
Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.
Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.
Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.
Упражнения и задачи для самостоятельного решения
1. Может ли прямая, не содержащая вершин замкнутой девятизвенной ломаной, пересечь каждое её звено?
2. (В. Произволов) Замкнутая ломаная такова, что каждые два её не соседних звена пересекаются. Докажите, что у этой ломаной нечётное количество звеньев.
3. Существует ли пятнадцатизвенная ломаная, пересекающая каждое своё звено ровно три раза?
4. Постройте восьмизвенную замкнутую ломаную, которая каждое своё звено пересекает один раз.
5. (Д. Калинин, вариация фольклора) Маша нарисовала замкнутую семизвенную ломаную. Для каждого звена она записала, со сколькими звеньями оно пересекается во внутренних точках. Могла ли она записать в каком-то порядке числа 1, 2, 3, 4, 3, 2, 1?
6. Какое наибольшее количество точек самопересечения может иметь замкнутая семизвенная ломаная?
7. (Н. Васильев) Рассматриваются всевозможные шестизвенные замкнутые ломаные, все вершины которых лежат на окружности.
САМОПЕРЕСЕЧЕНИЯ ТОЧКА
одна из особых точек кривой или поверхности. См., напр., Двойная точка.
Смотреть что такое «САМОПЕРЕСЕЧЕНИЯ ТОЧКА» в других словарях:
Самопересечения точка — узловая, кратная точка, одна из особых точек (См. Особая точка) кривой … Большая советская энциклопедия
Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия
Точка — I Точка (математическая) одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых… … Большая советская энциклопедия
Узловая точка — самопересечения точка, Особая точка кривой … Большая советская энциклопедия
УЗЛОВАЯ ТОЧКА — точка самопересечения кривой. При параметрич. задании кривой У. т. соответствует двум или более значениям параметра. Например, у кривой а sinЗj У. т. начало координат … Математическая энциклопедия
ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия
Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия
Особая точка — указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия
Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия
ДВОЙНАЯ ТОЧКА — один из видов особых точек кривой F(x, y) = 0, в к рой первые частные производные равны нулю и по крайней мере одна из вторых частных производных функции F(х, у)не равна нулю. При исследовании строения кривой вблизи Д. т. рассматривают знак… … Математическая энциклопедия
Точки самопересечения
Исследование и изображение кривой,
Заданной параметрически
Курсовая работа
| Курсовая работа защищена на оценку «_________ » «__»_________2014 г. | Исполнитель:Бажина Т.О., студентка Б-21 группы математического факультета очной формы обучения Руководитель:доктор физико-математических наук, профессор Мухин Ю.Н. |
Содержание
Исследование кривой…………………………………………………………5
2.Симметрия относительно осей координат, начала координат и прямой x=y
4.Точки пересечения с осями координат……………………………………….9
5. Поведение на концах области определения………………………………. 9
9.Вертикальные и горизонтальные касательные………………………………14
10.Обыкновенные точки, подозреваемые на перегиб…………………………16
11.Таблица поведения кривой…………………………………………………..18
Библиографический список источников…………………………………. 21
ВВЕДЕНИЕ
В доисторические времена человек наблюдал за природными явлениями, формой каких-либо предметов или физических тел. Лучи света, очертания стволов деревьев, листьев растений, линия горизонта, дуга радуги – все это непосредственно привлекало первобытных людей. Эти явления, наблюдаемые многократно, послужили основой для постепенного установления линии.
История развития изучения кривых обширна. Она захватывает почти 40 столетий и связана с именами таких великих математиков как Менехм, Архимед, Декарт, Брианшон, Паскаль, Штейнер, Шаль, Понселе и другие.
В настоящее время в курсах высшей математики широко освещаются методы построение графика функции. Вместе с тем построение кривых, задаваемых параметрически, уделяется мало внимания, и многие стороны этого более сложного исследования почти не затрагиваются. Как следствие, практическая работа, связанная с параметрически заданными кривыми и их построения, представляют собой определенные трудности. В связи с этим тема работы является актуальной.
Для нас, как для будущих учителей математики, исследование и изображение кривых является также немаловажным и выполняет первостепенные функции. Исследование кривой развивает аналитическое и логическое мышление, позволяет правильно конкретизировать мысли, излагая какой-либо научный материал. Навыки изображения кривой помогают решать задачи на построение. С помощью исследования методом дифференцирования развивается чувство абстрактности. А после построения кривой можно наглядно убедиться в правильности и точности всего исследования.
Таким образом, данная тема является особо актуальной для студентов педагогических ВУЗов математической направленности.
Цель исследования: освоить методы исследования и построения плоских кривых, заданных параметрическим способом в прямоугольной системе координат.
1.Изучить литературу по теме курсовой работы.
2. Провести исследование по данному плану.
3. Построить кривую.
Исследование кривой
Исследовать плоские кривые, заданные векторно. Изучить форму кривой:
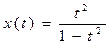
Область определения.
Областью определения называется множество, на котором задается функция.
Если задана функция, которая действует из одного множества в другое, то множество, из которого действует функция, называется областью определения.
Пусть задано отображение
Множество X называется областью определения функции f и обозначается D(f).
Если функция задана параметрически, то
Найдем область определения для нашей кривой:
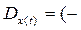













Таким образом, 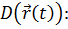
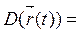






Область определения R, кроме t=
Получили, что кривая состоит из трёх ветвей
2.Симметрия относительно осей координат, начала координат и прямой y=x.
1) Симметрия относительно осей Ох и Oy.
Две точки А иА1 называются симметричными друг другу относительно прямойm, если прямаяm перпендикулярна отрезку АА1 и проходит через его середину. Прямую m называют осью симметрии.
При сгибании плоскости чертежа по прямойm – оси симметрии симметричные фигуры совместятся.
Симметрия относительно оси Ox:

Если x(t) 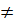
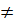
Симметрия относительно оси Oy:
Если x(t) 
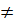
a) Относительно оси Ох. Достаточное условие симметрии:
Следовательно, кривая симметрична относительно оси Ох.
b) Относительно оси Оу. Достаточное условие симметрии:

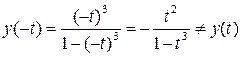
Таким образом, симметрия относительно Оy не установлена.
2) Симметрия относительно начала системы координат.
Достаточное условие симметрии:
Если x(t) 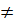
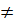
По доказанному ранее уже известно, что x(t) является четной функцией, т.е.
В связи с этим, симметрия относительно начала координат не установлена.
3) Симметрия относительно прямой у=х
Пусть М(х(t), y(t))
M´ симметрична М относительно прямой y=x
Тогда M 
Это означает, что существует t1:M 
t1 – функция от t должна быть биекцией D на себя, тогда

y(t) = x(t1)
Чтобы определить симметрию относительно прямой y=x, нужно решить следующую систему:

Если подставить в данную систему t = 
Точки самопересечения.
M (x(t), y(t)) называется точкой самопересечения, если существует такое значение параметра t, что
Чтобы найти точки самопересечения, решим следующую систему уравнений:


Разделим уравнение (1) на уравнение (2) почленно:

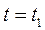

4. Точки пересечения с осями координат.
А) Найдем точки пересечения γ с осью Оy:
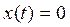
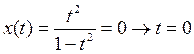
Итак, точка О (0;0) – точка пересечения γ с Оy.
Б) Найдем точки пересечения γ с осью ox:
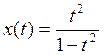

Итак, точка О (0;0) – точка пересечения γ с Ох.
Таким образом, имеем точку пересечения с осями координат: