Что такое сечение плоскости в геометрии

Что такое сечение плоскости в геометрии

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

.

Соединим точки P и L ( они лежат в одной плоскости).

.

Источник

Что такое сечение плоскости в геометрии

Автор видеоурока: к.пед.н., доцент кафедры ИГиСАПР Кайгородцева Н.В.

СЕЧЕНИЯ

На рис. 274, а показан чертеж рычага. Главный вид и вид сверху с двумя местными разрезами не выявляют форму его средней части. Форму средней части можно показать с помощью профильного разреза (рис. 274, б), но элементы, расположенные за секущей плоскостью, не дают дополнительную информацию о форме детали и являются лишними. В таких случаях удобно применять изображение, называемое сечением (рис. 274, в).

Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями, на сечении показывается только то, что расположено непосредственно в секущей плоскости.

В случае, показанном на рис. 274, вместо профильного разреза достаточно выполнить сечение (рис. 274, в). Применение сечений сокращает графическую работу при выполнении чертежа.

В отличие от разреза на сечении показывается только то, что расположено непосредственно в секущей плоскости, все, что лежит за ней, не изображается. На рис. 275 наглядно показано различие между сечением и разрезом.

Сечения в зависимости от расположения их на чертеже делятся на вынесенные и наложенные. Вынесенные сечения располагают на свободном месте поля чертежа (рис. 276, а) или в разрыве изображения предмета (рис. 276, в). Наложенные сечения располагают на соответствующем изображении предмета (рис. 276, б).

Предпочтительны вынесенные сечения. Их контур вычерчивают сплошными толстыми линиями (рис. 276, а). Контуры наложенных сечений вычерчивают сплошными тонкими линиями.

В случаях, подобных показанным на рис. 276, при симметричной фигуре сечения положение секущей плоскости не указывается.

Для несимметричных сечений, расположенных в разрыве или наложенных, положение секущей плоскости указывается линией сечения со стрелками, но буквами не обозначается (рис. 277, а и б).

Во всех остальных случаях выполнения сечений положение секущей плоскости должно быть показано линией сечения с указанием стрелками направления взгляда, а над самими сечениями выполняется надпись (рис. 278, а и б).

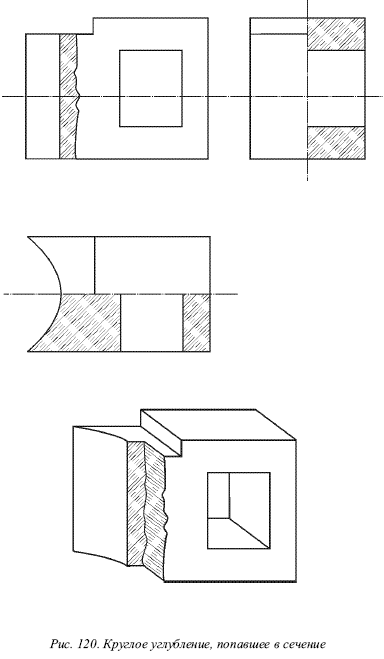
При совпадении секущей плоскости с осью поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубления в сечении показывается полностью, хотя этот контур и не расположен в секущей плоскости (рис. 277, в, см. стрелки К), т. е. сечение оформляется как разрез. Если секущая плоскость проходит через некруглые отверстия (рис. 279, а) и сечение получается состоящим из отдельных частей (рис. 279, б), то сечение должно быть заменено разрезом (рис. 279, в).

Сечение может выполняться несколькими секущими плоскостями, как на рис. 279, г.

Допускается вместо секущих плоскостей применять секущие цилиндрические поверхности, развертываемые затем в плоскость. На рис. 280 деталь имеет различные отверстия. Форму этих отверстий удобно выявить, применяя развернутое сечение детали секущей цилиндрической поверхностью, указанной линией сечения со стрелками и буквами. Над развернутым сечением выполняется надпись теми же буквами с добавлением слова «развернуто».

ВЫНОСНЫЕ ЭЛЕМЕНТЫ

В тех случаях, когда на основном изображении невозможно изобразить мелкие элементы изделия со всеми подробностями, применяют выносные элементы.

Выносным элементом называют дополнительное отдельное изображение в увеличенном виде какой-либо части изделия, требующей графического и других пояснений в отношении формы, размеров и иных данных.

При применении выносного элемента соответствующее место изображения отмечают замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением римской цифрой порядкового номера выносного элемента на полке линии-выноски (рис. 281).

Над выносным элементом указывается та же цифра и масштаб, в котором выполнен выносной элемент (масштабы могут быть различные).

Выносной элемент следует располагать возможно ближе к соответствующему месту на изображении предмета. Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию. Например, изображение может быть видом, а выносной элемент — разрезом.

Источник

Инженерная графика

Сечение геометрических тел плоскостями

Понятие о сечении и линии пересечения

В результате пересечения геометрического тела плоскостью получается плоская фигура, которую называют сечением (или фигурой сечения).

В общем случае сечение представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности тела.

При пересечении плоскостью многогранных геометрических тел (призмы, пирамиды, параллелепипеда и т. п.) в общем случае получается замкнутая ломаная линия, состоящая из отдельных отрезков прямых линий, точки излома линии пересечения являются точками пересечения ребер многогранной фигуры плоскостью.

Если фигура представляет собой тело вращения (цилиндр, конус, шар и т. п.) или ее поверхность ограничена плавными кривыми поверхностями, линией сечения будет кривая, для построения которой необходимо определить характерные точки, расположенные на очерковых образующих, точки, удаленные на максимальное и минимальное расстояние от плоскости проекции, а также произвольные точки линии сечения. При этом чем больше точек пересечения плоскостью такой фигуры будет определено, тем правильнее будет построена линия пересечения.

Пересечение тел проецирующими плоскостями.
Построение действительной величины фигуры сечения.

При пересечении геометрических тел плоскостью проецирующего положения (т. е. перпендикулярной одной из плоскостей проекции) одна из проекций сечения изображается прямой линией, совпадающей с линейной (вырожденной) проекцией плоскости, т. е. сечение фигуры на этом виде представляет собой прямую, которая может быть параллельна какой-либо оси проекций (х, у или z), либо располагаться под наклоном к ней. Остальные проекции сечения определяют по характерным точкам пересечения плоскости с ребрами фигуры методом прямоугольного проецирования.

Пересечение многогранников плоскостью

При пересечении многогранника плоскостью частного положения грани будут пересекаться по прямым линиям, и линией пересечения будет замкнутая или незамкнутая ломаная линия. Для построения этой линии достаточно найти точки пересечения ребер с заданной плоскостью (опорные точки) и соединить их с учетом видимости.

Пример пересечения призмы плоскостью

Задача

Построить линию пересечения призмы ABCD плоскостью а (рис. 1). Определить действительную величину фигуры сечения.

Решение.

Пример пересечения пирамиды плоскостью

Задача

Построить линию пересечения пирамиды плоскостью а (рис. 2). Определить действительную величину сечения.

Решение

Т. к. плоскость а фронтально-проецирующая, то не требуется дополнительных построений. Фронтальный след плоскости совпадает с фронтальной проекцией сечения.
На пересечении ребер с фронтальным следом плоскости находим точки 7…4, линии сечения.
По точкам 7, 2, 3 и 4 на ребрах пирамиды строим горизонтальную и профильную линию сечения.
Действительную величину сечения 7-2-3-4 определяем способом замены плоскостей проекций.
Порядок построения показан на рис. 2. Фигура 1-4 и есть действительная величина сечения.
Выполняем третью проекцию по координатам точек вершин. Соединив полученные точки прямыми линиями, получаем третью проекцию пирамиды с линией пересечения плоскостью.

Пересечение поверхностей вращения плоскостью

Пересечение цилиндра плоскостью

В сечении цилиндра плоскостью частного положения могут быть получены следующие линии (рис. 3):

Задача

Построить линию пересечения прямого кругового цилиндра фронтально проецирующей плоскостью а (рис. 4). Определить действительную величину сечения.

Решение

Пересечение прямого кругового конуса плоскостью

Чтобы получить в сечении получился эллипс, плоскость должна пересекать все образующие конической поверхности. В частном случае, когда диаметры равны (секущая плоскость перпендикуляра оси конической поверхности), в сечении получается окружность (рис. 5, а).

Чтобы в сечении получить параболу, секущая плоскость должна быть параллельна одной из образующих конуса. В пределе, когда секущая плоскость переходит в касательную, две симметричные дуги параболы преобразуются в две совпадающие прямые (рис. 5, б).

Гипербола в сечении получается, если секущая плоскость параллельна двум прямолинейным образующим конуса.
В частном случае, когда секущая плоскость проходит через вершину конической поверхности, гипербола распадается на две пересекающиеся прямые (рис. 5, в).

Пример построения действительной фигуры сечения и линии пересечения конуса плоскостью показан на рис. 6.

Источник

Методы построения сечений многогранников

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Источник

Что такое сечение плоскости в геометрии

Лекция № 14. Сечения и разрезы

Существуют некоторые определения и правила, которые относятся к сечениям.

Сечение – это плоская фигура, которая была получена в результате пересечения данного тела некоторой секущей плоскостью. При этом след секущей плоскости проводится штрихпунктирной линией. Выбирая такое направление секущих плоскостей, лучше избегать косых сечений, чтобы получались нормальные поперечные сечения тела.

Площадь сечения покрывается штриховкой, причем линии штриховки должны составлять угол в 45° с осевыми линиями или с основными линиями контура. Здесь же наклон и расстояния между линиями должны сохраняться неизменными, а штриховка различных сечений одного и того же тела должна выполняться одинаково. Толщина линий штриховки не должна превышать одной четверти толщины линии контура, т. е. b/4 и менее. При этом заштрихованное сечение не должно бросаться в глаза толщиной линий штриховки или чрезмерной их густотой. В том случае, если осевая линия детали или линия ее контура расположена под углом 45° к осевой линии, принятой за основную на данном чертеже, штриховку выполняют под углом 30° или 60° к основной осевой линии чертежа.

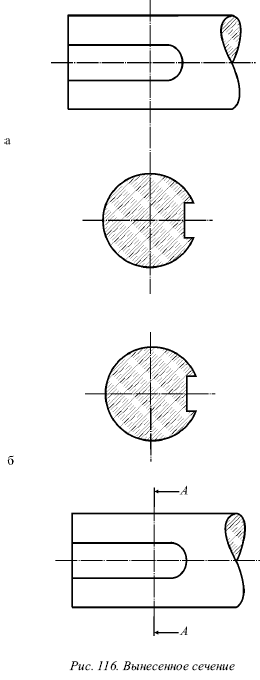
На рисунке 116 показано, что контур детали и контур вынесенного сечения имеют одинаковую толщину: а) расположение вынесенного сечения на продолжении следа секущей плоскости; б) вынесенное сечение, расположенное на произвольном месте чертежа, сопровождается соответствующей подписью.

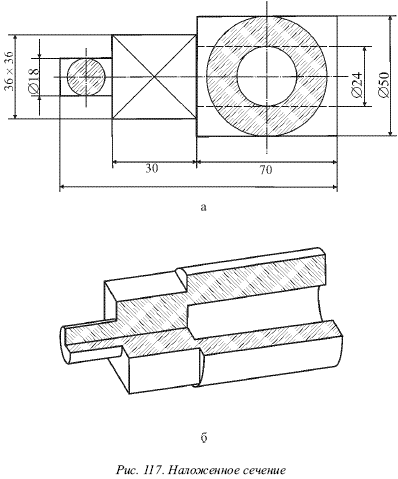
Сечения бывают вынесенными (рис. 116) и наложенными (рис. 117а). Рекомендуется выполнять вынесенные сечения, а наложенные не рекомендуются.

Контур вынесенного сечения и контур самой детали должны иметь одинаковую толщину b.

Вынесенные сечения должны располагаться на продолжении следа секущей плоскости (рис. 117а). Это сечение может быть расположено в разрыве между частями одного и того же вида. Данное сечение допускается располагать в произвольном месте чертежа (рис. 117б), тогда след секущей плоскости отмечается парой одинаковых букв русского алфавита, а над сечением ставится соответствующая надпись (рис. 117б). Если имеется нескольких сечений, то буквы следует брать в алфавитном порядке без повторений.

Для несимметричных сечений при совмещении их с плоскостью чертежа нужно:

1) вращать их слева направо, если след секущей плоскости находится вертикально (рис. 117а);

2) вращать их на себя, если след секущей плоскости размещен горизонтально.

Наложенные сечения (рис. 117) обводятся тонкими сплошными линиями, т. е. b/4 и менее, при этом толщина контура наложенного сечения примерно в четыре раза тоньше контура детали.

Определения и правила, которые относятся к разрезам.

Разрез – это такое условное изображение предмета, когда его часть, находящаяся между глазом наблюдателя и секущей плоскостью, мысленно удалена, и вычерчивается то, что находится в секущей плоскости и расположено за ней.

Площадь сечения должна покрываться штриховкой, которая при различных сечениях одного и того же тела выполняется одинаково, а наклон и расстояния между линиями остаются неизменными.

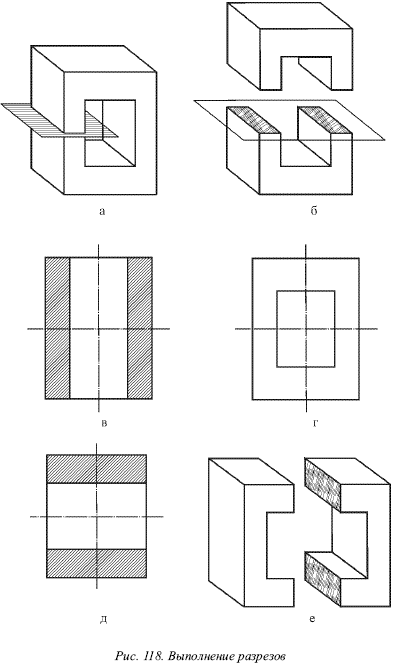
Классификация разрезов. В зависимости от положения секущей плоскости различают следующие разрезы (рис. 118):

1) вертикальные, если секущая плоскость вертикальна (вид слева, 118д);

2) горизонтальные, если секущая плоскость горизонтальна (план, 118в);

3) наклонные, если секущая плоскость наклонена к горизонтальной плоскости.

Вертикальные разрезы следует располагать соответственно на месте главного вида, вида слева и вида справа, а горизонтальные разрезы – на месте вида сверху и вида снизу (рис. 118).

Разрезы, выполняемые при изображении данного предмета, не зависят один от другого, все эти разрезы выполняются независимо друг от друга. Представляемые действия, которые мы выполняем для получения разреза на одной проекции, никак не отражаются на другой проекции.

Симметричные проекции. Если разрез является симметричной фигурой, то можно вместо целого разреза вычерчивать несколько более его половины. Если изображаемый предмет проецируется в виде симметричной фигуры, тогда вполне возможно соединить половину внешнего вида с половиной разреза. При этом разрез помещают справа от вертикальной оси симметрии или под горизонтальной осью.

Осевая линия должна служить разделом между половиной внешнего вида и половиной разреза. Если сделать ее сплошной это будет грубой ошибкой. Толщина штрихпунктирной линии должна составлять b/4 и менее.

Внутренние линии, выявленные на разрезе, не повторяют штриховой линией на симметричной половине проекции.

Также избегают лишние штриховые линии, не делают бесполезных разрезов.

В случае несимметричной проекции нельзя соединить половину внешнего вида с половиной разреза.

Несимметричные проекции. На несимметричных проекциях можно сделать полный разрез, тогда внешний вид тела будет отсутствовать.

След секущей плоскости. Когда следы секущей плоскости совмещаются с осями симметрии проекций, то нет необходимости в дополнительных обозначениях на чертежах. В случае если след секущей плоскости не совпадает с осью симметрии данного вида, тогда он должен отмечаться утолщенными штрихами в начале и в конце линии разреза. В этом случае штрихи, которые обозначают начало и конец линии разреза, должны заходить за линию контура на 2–3 мм. Штрихи должны обозначаться прописными буквами русского алфавита, и разрезом должна быть сделана соответствующая подпись. При этом буквы выбирают таким образом, что каждая секущая плоскость обозначалась одной и той же буквой у начала и у конца линии разреза.

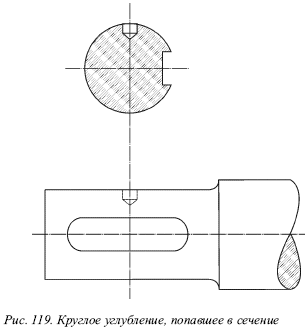
Сочетание сечения с разрезом. В случае если при выполнении сечения в секущую плоскость попадает цилиндрическое, коническое, шаровое и подобное круглое отверстие или углубление, то контур отверстия или углубления вычерчивается по типу разреза (рис. 119).

3. Частичный разрез или вырыв

Разрез называется полным, если изображаемый предмет рассекается целиком, остальные разрезы называются частичными, или вырывами. На рисунке 120 на виде слева и на плане сделаны полные разрезы. Причем на каждой проекции была соединена половина внешнего вида с половиной разреза. Нет смысла делать полный разрез на главном виде, поскольку нужно было бы напрасно разрезать толщину всего тела. Поэтому на главном виде был сделан частичный разрез (или вырыв). С его помощью стала видна находящаяся слева выемка. Благодаря этому освободилась большая часть проекции тела от ненужной штриховки. Следует иметь в виду, что границы вырыва указываются линией специального вида – линией вырыва, которая не должна совпадать с линией контура или быть ее продолжением.

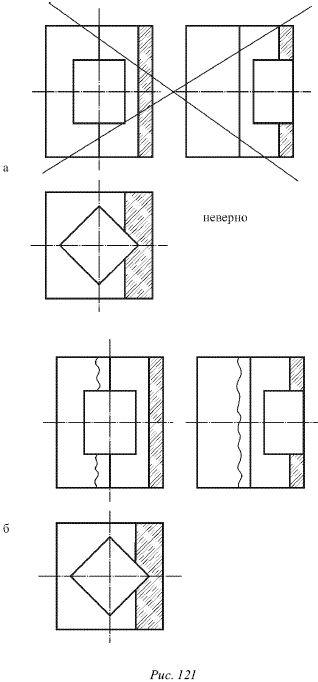
Частичный разрез симметричных фигур. В случае, если на оси симметрии проекции находится контурная линия, нельзя около этой оси симметрии соединять половину внешнего вида с половиной разреза (рис. 121а), тогда часть внешнего вида отделяется от разреза линией вырыва (рис. 121б).

Если соединить половину вида с половиной разреза (рис. 121а), то такой чертеж может привести к недоразумениям, поскольку непонятно, относится эта контурная линия к внешнему виду или к внутренней полости. Здесь нужно соединить часть вида с частичным разрезом (рис. 121б) или расположить разрезы на нижних половинах проекций.

На рисунке 121. Нельзя соединять половину внешнего вида с половиной разреза около оси симметрии, если на ней имеется контурная линия (а). В этом случае надо часть внешнего вида соединить с частичным разрезом (б).

Отсутствие линии вырыва. В отдельных случаях, при выполнении частичного разреза, можно не проводить линию вырыва, а ограничиться лишь штриховкой разрезанной части (рис. 123).

4. Простые и сложные разрезы

Разрезы различают в зависимости от числа секущих плоскостей, при помощи которых получается разрез на данной проекции. Они бывают:

1) простыми, когда имеется только одна секущая плоскость;

2) сложными, когда имеются две или более секущие плоскости, которые совмещаются с данной плоскостью проекций.

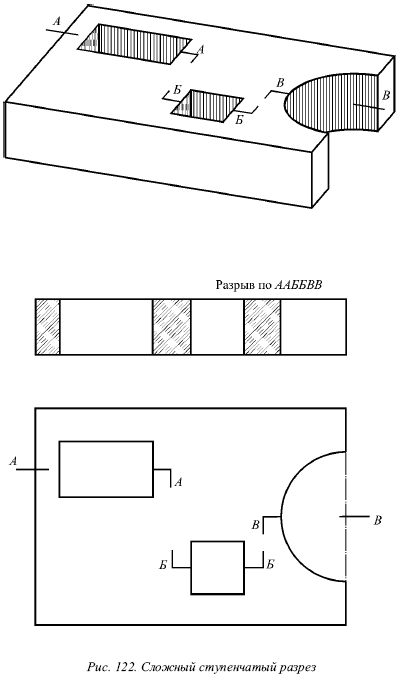
Ступенчатым называется разрез в том случае, если сложный разрез получается при помощи параллельных плоскостей.

На рисунке 122 сложный ступенчатый разрез показан при помощи трёх фронтальных плоскостей.

Линия разреза. Если след секущей плоскости на сложных разрезах не совпадает с осью симметрии проекции, то он отмечается штрихами в начале, в местах излома и в конце линии разреза (рис. 122). Буквы для обозначения разрезов берут в алфавитном порядке и не допускают их повторения на одном и том же чертеже.

Источник