Что такое сечение призмы плоскостью

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Сечения призмы (справочный материал).

Справочный материал по теме «Сечение призмы».

Просмотр содержимого документа
«Сечения призмы (справочный материал).»

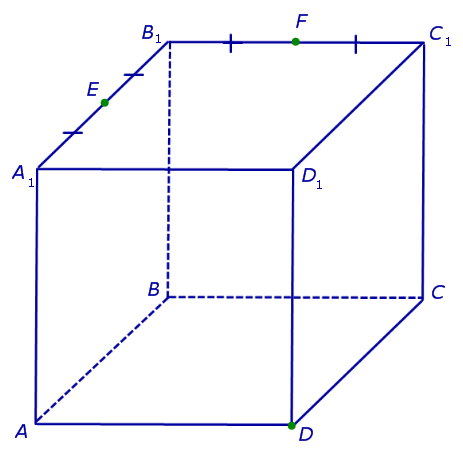
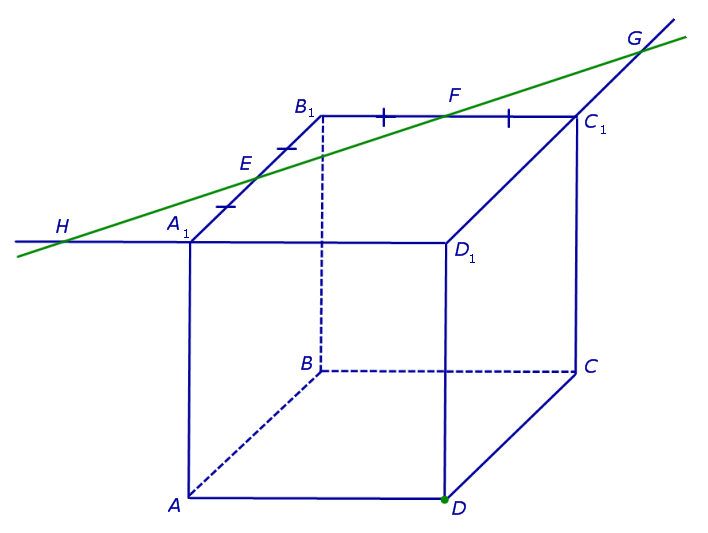
Определение 1. Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости α.

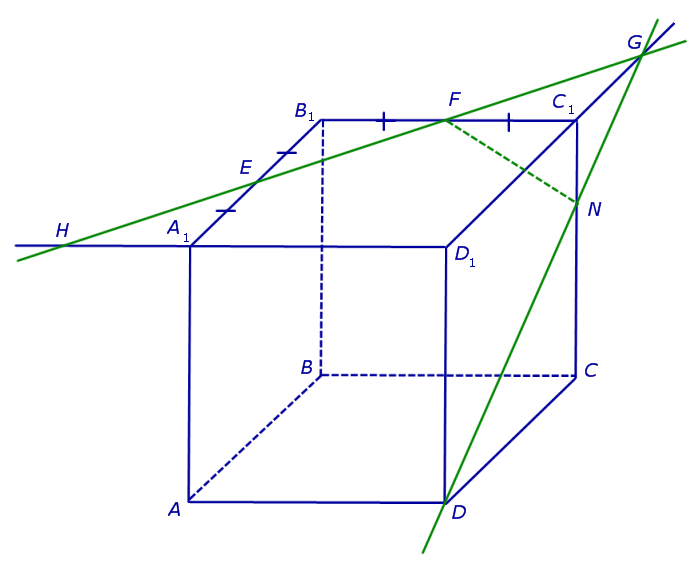
Точки G и D принадлежат плоскости сечения, а, значит, и вся прямая DG лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба DD₁C₁C. Значит, точка пересечения DG с ребром куба C₁C (точка N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения: FN и DN (рис. 3).

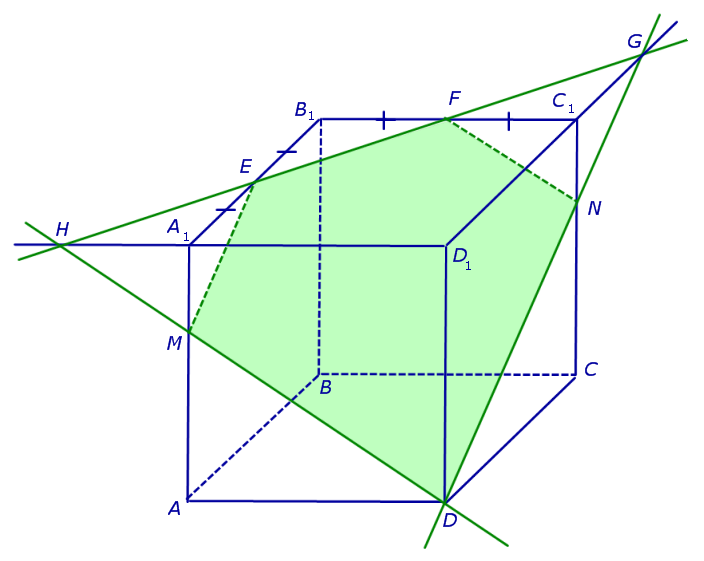
Теперь, действуя аналогичным образом, проводим прямую HD, обозначаем точку перечения этой прямой с ребром AA₁ буквой M и проводим линии сечения ME и MD в плоскостях граней AA₁B₁B и AA₁D₁D (рис. 4).

В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник DMEFN.

Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.

Задача. Наши площадь сечения DMEFN, если ребро куба равно 6.

Перпендикулярные сечения призмы

Определение 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.

На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник KLM. Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.

Источник

Сечения призмы (11 класс)

Описание презентации по отдельным слайдам:

Сечения призмы Подготовил учитель математики, МБОУ СОШ №12, города Воронежа, Кузнецова Светлана Владимировна

Для решения многих геометрических задач, необходимо уметь строить сечения призмы различными плоскостями

Плоская фигура, образовавшаяся при пересечении какой-либо плоскости с пространственной фигурой, называется плоским сечением или просто сечением этой фигуры.

Сечением призмы является многоугольник, вершины которого расположены на ребрах, а стороны целиком лежат на гранях.

Вид сечения зависит от расположения плоскости

Сечения призмы плоскостями, параллельными боковым ребрам, являются параллелограммами В частности параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими через два боковых ребра, не принадлежащей одной грани.

Что значит построить сечение? Построить сечение призмы плоскостью – означает: В плоскости каждой пересекаемой грани многогранника указать 2-е точки, принадлежащие сечению; Соединить их прямой; Найти точки пересечения прямой с ребрами призмы.

Методы построения сечений призм Метод следов Метод внутреннего проектирования или метод вспомогательных сечений Комбинированный метод

Метод следов Если плоскость пересекает плоскость по прямой S, то прямую S называют следом плоскости на плоскость

Метод следов Метод следов включает три важных пункта: Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника. Находим точки пересечения секущей плоскости с ребрами многогранника. Строим и заштриховываем сечение.

Задача для самостоятельного решения. Призма ABCDA1B1C1D1. Построить сечение, проходящее через точки M, N, L.

Куда еще можно обратиться, чтобы узнать больше об этом вопросе. Адрес ссылки Краткое содержание http://www.freeware.ru/program_prog_id_1536.html Программа 3D SecBuilder строит сечение основных пространственных тел. «СТЕРЕОМЕТРИЯ. Электронный учебник-справочник» серия»Домашний компьютер и школа»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-403713

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге школьникам разрешили уйти на каникулы с 25 декабря

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

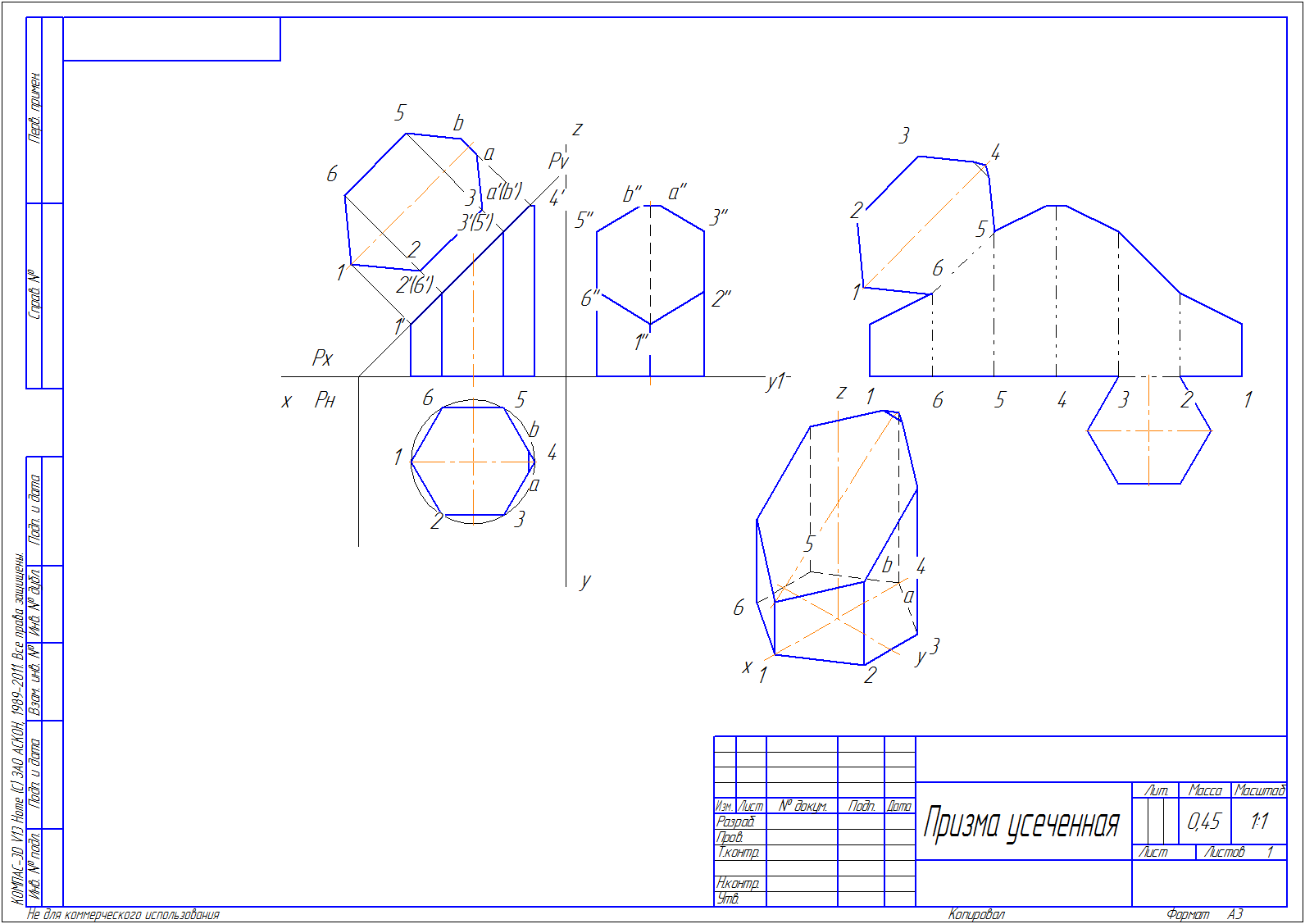
Урок 6. Сечение призмы плоскостью. Развертка усеченной призмы.

Здравствуйте! Сегодня мы коснемся такой темы, как сечение призмы плоскостью и построим развертку усеченной призмы в Компасе.

Последовательность построения чертежа усеченной призмы

1. Создаем чертеж, меняем формат на А3.

2. На компактной панели активируем инструментальную панель «Виды», выбираем «Стандартные виды».

4. Проводим осевые линии.

5. От центра симметрии призмы откладываем расстояние до следа секущей плоскости. В нашем примере это 37 мм. Из полученной точки проводим след секущей плоскости Pv под углом 45º

6. Обозначаем точки пересечения секущей плоскости с ребрами призмы на фронтальной проекции призмы и по линиям связи находим эти точки на оставшихся проекциях. Таким образом, получаем искаженные фигуры сечения призмы плоскостью в проекциях.

7. Но нам необходимо знать, как выглядит натуральный вид сечения призмы или действительная величина контура сечения. Строим его.

Построение натурального вида сечения призмы

8. Для построения из каждой точки фронтальной проекции поднимаем перпендикуляры.

9. Переносим соответствующие размеры с горизонтальной проекции призмы на новую горизонтальную проекцию (т. к. натуральный вид сечения мы строим способом перемены плоскостей проекций).

Развертка усеченной призмы

10. Развертку усеченной призмы будем строить на одной линии координатными осями проекций призмы. Так будет меньше вспомогательных построений.

11. Сначала строим отрезок длиной, равной длине всех 6 ребер призмы, получается 120 мм.

12. Делим этот отрезок на 6 частей, нумеруем.

13. При помощи вспомогательных линий переносим высоты ребер усеченной призмы, соединяем вершины отрезков.

14. Действительную фигуру сечения переносим на развертку путем копирования (ctrl+выделяем левой кнопкой мыши), достраиваем нижнее основание призмы. Линии сгиба обозначаем специальной линией, она в Компасе называется – пунктир 2.

Строим изометрию усеченной призмы

15. Изометрию будем строить вручную, т. е. все операции построения в точности повторяют черчение аксонометрии на бумаге.

16. Проводим две вспомогательные линии под углами 30 и 150 градусов, строим изометрию нижнего основания – шестиугольник, нумеруем их.

17. Затем из каждой вершины шестиугольника поднимаем отрезки, высотой, равной высоте соответствующих отрезков на фронтальной проекции призмы. Соединяем точки. Изометрия готова.

18. Теперь остается только оформить чертеж в соответствии с требованиями и заполнить основную надпись.

Весь процесс создания чертежа усеченной призмы подробно рассмотрен в небольшом видеоуроке.

Теперь вы без труда построите сечение призмы плоскостью и развертку усеченной призмы.

Источник

Сечение геометрических тел плоскостями и развертки их поверхностей с примерами и образцами выполнения

Содержание:

Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок. Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией.

Понятие о сечениях геометрических тел

Детали машин и приборов очень часто имеют формы, представляющие собой различные геомет­рические поверхности, рассеченные плоскостями (рис. 175). Кроме того, иногда необходимо выпо­лнить развертки поверхности полых деталей, усе­ченных плоскостью. Это применяется в раскрое листового материала, из которого изготовляются полые детали. Такие детали обычно представляют собой части всевозможных трубопроводов, венти­ляционных устройств, кожухов для закрытия механизмов, ограждения станков и т.п. (рис. 176)

Построения прямоугольных и аксонометричес­ких проекций усеченных тел, а также определе­ние истинного вида сечений и разверток повер­хностей геометрических тел часто используются на практике.

Рассекая геометрическое тело плоскостью, по­лучают сечение — ограниченную замкнутую линию. все точки которой принадлежат как секущей плоскости, так и поверхности тела.

При пересечении плоскостью многогранника (например, призмы, пирамиды) в сечении получа­ется многоугольник с вершинами, расположенны­ми на ребрах многогранника. При пересечении плоскостью тел вращения (например, цилиндра, конуса) фигура сечения часто ограничена кривой линией. Точки этой кривой находят с помощью вспомогательных линий — прямых или окружнос­тей, взятых на поверхности тела. Точки пересечения этих линий с секущей плоскостью будут искомыми точками контура криволинейного сече­ния.

Пример сечения плоскостью Р геометрического тела — куба, лежащего на горизонтальной плос­кости проекции Н, показан на рис. 177.

В первом случае (рис 177, а) куб усечен фронтально-проецирующей плоскостью Р. Фигурой сечения является прямоугольник.

При построении двух проекций такого сечения (рис. 177, б) следует иметь в виду, что фронталь­ная проекция фигуры сечения совпадает с фрон­тальным следом секущей плоскости Р_V.

Горизонтальная проекция фигуры сечения — прямоугольник.

Во втором случае (рис. 177, в) куб усечен горизонтально-проецирующей плоскостью Р. Фигура сечения — прямоугольник.

На рис. 177, г приведено построение проекции этого сечения. Горизонтальная проекция фигуры сечения совпадает с горизонтальным следом Р_Н секущей плоскости. Фронтальной проекцией сече­ния будет прямоугольник, одной стороной которо­го является линия пересечения плоскости Р с плоскостью передней грани куба.

Если куб пересечен плоскостью общего положе­ния (рис. 177, д, е), то полученная фигура сече­ния в данном случае (треугольник) проецируется на плоскости проекции V и H с искажением.

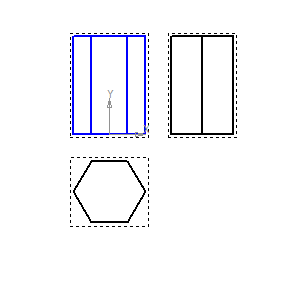
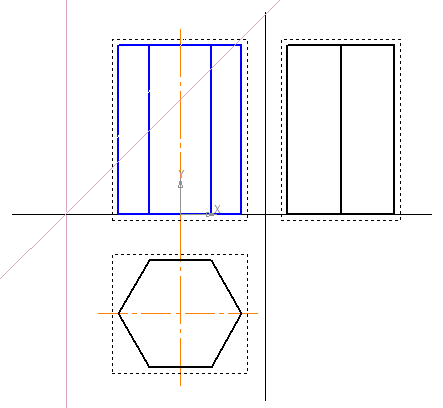
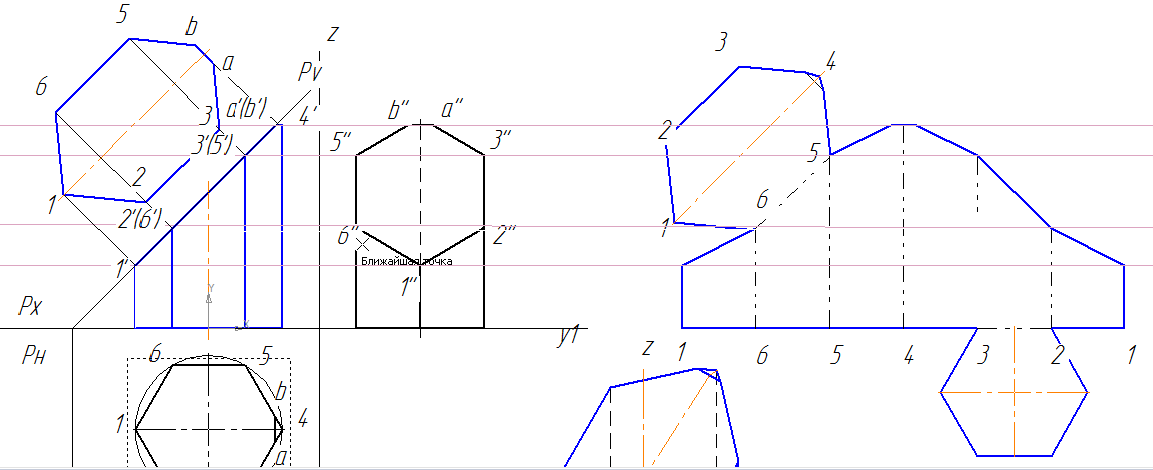
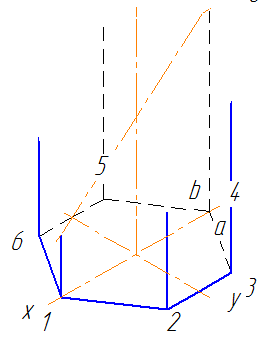
Сечение призмы плоскостью

Для построения проекций фигуры сечения на­ходят проекции точек пересечения плоскости Р с ребрами призмы и соединяют их прямыми линия­ми. Фронтальные проекции этих точек получают­ся при пересечении фронтальных проекций ребер призмы с фронтальным следом P_V секущей плос­кости Р (точки 1’. 5′).

Горизонтальные проекции точек пересечения 1. 5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1»…5». Полученные точки 1»…5» соединяют пря­мыми линиями и получают профильную проекцию фигуры сечения.

Действительный вид фигуры сечения можно определить любым из способов: вращения, совме­щения или перемены плоскостей проекций (см. гл. 15).

В данном примере (рис. 178, а) применен способ перемены плоскостей проекций. Гори­зонтальная плоскость проекций заменена но­вой Н₁, причем ось х₁ (для упрощения по­строений) совпадает с фронтальным следом плоскости Р.

Разверткой называется плоская фигура, полу­ченная при совмещении поверхности геометричес­кого тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Развертку боковой поверхности (рис. 178, б) с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на кото­рой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпен­дикуляры, на которых откладывают действитель­ные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции (рис. 178, а), получают развертку боковой повер­хности призмы.

К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод три­ангуляции (см. рис. 50, б) или метод координат, известный из геометрического черчения. На рис. 178, а показано построение вершины 5 метолом триангуляции. Линии сгиба по ГОСТ 2.303-68 показывают на развертке штрихпунктирной линией с двумя точками.

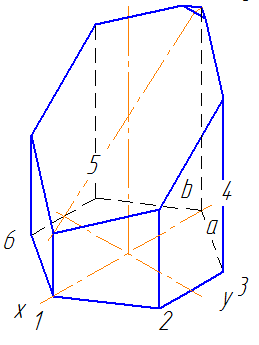
Для наглядности выполним построение усечен­ного тела в аксонометрической проекции. На рис. 178, в построена изометрическая проекция усеченной призмы. Порядок построения изометри­ческой проекции следующий. Строят изометричес­кую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на кото­рых от основания откладывают их действительные длины, взятые с фронтальной или профильной проекции призмы. Полученные точки сое­диняют прямыми линиями.

Сечение цилиндра плоскостью

Построение сечения прямого кругового цилин­дра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматри­вать как прямую призму с бесчисленным множес­твом ребер — образующих цилиндра (рис. 179, а).

Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равно­мерно расположенных образующих, в данном примере двенадцать. Для этого горизонтальную проекцию основания делят па 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рис. 179, а).

Из комплексного чертежа видно, что плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилин­дра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рис. 179, в).

Фронтальная проекция фигуры сечения совпа­дает с фронтальным сладом Р_V плоскости Р. Гори­зонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра.

Профильная проекция фигуры сечения пред­ставляет собой проекцию части эллипса и может быть построена по нескольким точкам, которые строятся с помощью линий связи по горизонталь­ной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.

Действительный вид фигуры сечения получен на рис. 179, а способом перемены плоскостей про­екций. Горизонтальная плоскость проекций заме­нена новой. Новая ось проекций x₁ может быть проведена параллельно следу Р_V на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с Р_V (аналогично рис 178). От оси x₁ откладывают отрезки 5’5₀ = 55_x, 4’4₀ = 44_x, т.е. отрезки т, п и т.д., так как расстояние от новой проекции этой точки до но­вой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекции.

Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения пока­зана на рис. 179, б.

Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания, равную πD и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку πD, на них откладыва­ют действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 1₁—9₁ соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой l₁9₁ (сегмент), а фигуру нижнего основания цилиндра (окружность) соеди­няют с нижней частью развертки.

Изометрическую проекцию усеченного цилин­дра строят следующим образом (рис. 179, в). Сна­чала строят изометрию нижнего основания (овал) и части верхнего основания — сегмента (часть овала). На диаметре окружности нижнего основа­ния от центра О’ откладывают отрезки а, b и т.д., взятые с горизонтальной проекции основания. Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересечения с осью эллипса.

Через полученные точки проводят прямые, параллельные оси у, и на них откладывают отрез­ки, взятые с действительного вида сечения. Полу­ченные точки соединяют но лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям — овалам.

Пылесборник машины для очистки литых дета­лей (рис. 179, г) представляет собой усеченный цилиндр. Форма крышки А трубы пылесборника является фигурой сечения прямого кругового ци­линдра и представляет собой эллипс.

Сечение пирамиды плоскостью

Правильная шестиугольная пирамида, пересе­ченная фронтально-проецирующей плоскостью Р, показана на рис 180.

Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным сле­дом Р_V плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, кото­рые являются точками пересечения плоскости Р с ребрами пирамиды.

Действительный вид фигуры сечения в этом примере определяется способом совмещения.

Развертка боковой поверхности усеченной пи­рамиды с фигурой сечения и фигурой основания приведена на рис. 180, б.

Сначала строят развертку неусеченной пирами­ды, все грани которой, имеющие форму треуголь­ника. одинаковы. На плоскости намечают точку s₁ (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s»e» или s»b», так как зги ребра парал­лельны плоскости W и изображаются на ней дей­ствительной длиной. Далее по дуге окружности от любой точки, например а₁, откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пира­миды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab).Точки а₁… f₁ соединяют прямыми с вершиной s₁. Затем от вершины а₁ на этих пря­мых откладывают действительные длины отрезков ребер до секущей плоскости.

На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — s»5 и s»2. Действительные длины ос­тальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину s. Например, повер­нув отрезок s»6« около оси до положения, парал­лельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6″ провести горизонтальную прямую до пересечения с действительной длиной ребра SE или SB. Отрезок s»6« ₀ (см. рис. 180).

Полученные точки 1₁, 2₁, 3₁ и т.д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.

Построение изометрической проекции усечен­ной пирамиды начинают с построения изометри­ческой проекции основания пирамиды по разме­рам, взятым с горизонтальной проекции комплек­сного чертежа. Затем на плоскости основания по координатам точек 1. 6 строят горизонтальную проекцию сечения (см. тонкие синие линии на рис. 180, а, в). Из вершин полученного шести­угольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фронтальной или профильной проекций призмы, на­пример, отрезки К₁ К₂, К₃ И т.д. Полученные точки I. 6 соединяем, получаем фигуру сечения. Соединив точки 1. 6 с вершинами шестиугольни­ка, основания пирамиды, получим изометричес­кую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.

Пример сечения треугольной неправильной пирамиды фронтально-проецируемой плоскостью показан на рис. 181.

Все ребра на трех плоскостях проекций изображены с искажением. Горизонтальная проекция основания представляет собой его действительный вид, так как основание пирамиды расположено на плоскости Н.

Действительный вид 1₀, 2₀, 3₀ фигуры сечения получен способом перемены плоскостей проекций. В данном примере горизонтальная плоскость про­екций Н заменена новой плоскостью, которая параллельна плоскости Р\ новая ось х₁ совмещена со следом (рис. 181, а).

Развертку поверхности пирамиды строят следу­ющим образом. Способом вращения находят дей­ствительную длину ребер пирамиды и их отрезков от основания до секущей плоскости Р.

Например, действительные длины ребра SC и его отрезка СЗ равна соответственно длине фрон­тальной проекции s’с’ ребра и отрезка с’₁ 3₁ после поворота.

Затем строят развертку треугольной неправиль­ной пирамиды (рис. 181, в). Для этого из произвольной точки S проводят прямую, на которой откладывают действительную длину ребра SA. Из точки s делают засечку радиусом R₁ равным действительной длине ребра SB ,а из точки А — засечку радиусом R₂, равным стороне основания пирамиды AB, в результате чего получают точку b₁ и грань s₁b₁а₁ пирамиды. Затем из точек s и b₁, как из центров, делают засечки радиусами, равными действительной длине ребра SC и его стороне ВС, и получают грань s₁b₁c₁ пирамиды. Также строится грань s₁с₁а_1.

Для построения изометрической проекции усе­ченной пирамиды (рис. 181. б) проводят изомет­рическую ось х. По координатам т и п строят основание пирамиды АВС. Сторона основания АС параллельна оси х или совпадает с осью х. Как и в предыдущем примере, строят изометрическую проекцию горизонтальной проекции фигуры сече­ния 1₂2₂3₂ (используя точки I, III и IV). Из этих точек проводят вертикальные прямые, на которых откладывают отрезки, взятые с фронтальной или профильной проекции призмы К₁, К₂ и К₃. Полу­ченные точки 1, 2. 3 соединяют прямыми между собой и с вершинами основания.

Сечение прямого кругового конуса плоскостью

В зависимости от расположения секцией плос­кости Р относительно оси прямого кругового кону­са получаются различные фигуры сечения, ограниченные кривыми линиями.

Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рис. 182. Основание конуса расположено на плос­кости Н. Фигура сечения в данном случае будет ограничена эллипсом.

Фронтальная проекция фигуры сечения распо­ложена на фронтальном следе плоскости Р (рис. 182. а).

Для построения горизонтальной проекции кон­тура фигуры сечения горизонтальную проекцию основания конуса (окружности) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях прово­дят вспомогательные образующие. Сначала нахо­дят фронтальные проекции точек сечения 1‘. 12’, лежащих на плоскости Р₁. Затем с по­мощью линии связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей s2, прое­цируется на горизонтальную проекцию этой же образующей в точку 2.

Найденные горизонтальные проекции точек контура сечения соединяют по лекалу. Действи­тельный вид фигуры сечения в данном примере найден способом перемены плоскости проекции. Плоскость H заменяется новой плоскостью проек­ции H₁.

На фронтальной плоскости проекции V фигура сечения — эллипс изображается в виде прямой 1’7′, совпадающей с фронтальной проекцией секущей плоскости Р. Эта прямая 1’7’ является большой осью эллипса. Малая ось эллипса а’Ь’ перпендикулярна к большой оси 1’7′ и проходит через ее середину. Чтобы найти малую ось сече­ния, через середину большой оси 1’7′ эллипса проводят горизонтальную плоскость N, которая рассечет конус по окружности, диаметр которой будет равняться малой оси эллипса (a₀b₀).

Построение развертки поверхности конуса (рис. 182, б) начинают с проведения дуги окружности радиусом, равным длине образующей кону­са из точки s₀. Длина дуги определяется углом α:

Дугу делят на 12 частей и полученные точки соединяют с вершиной s₀. От вершины откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.

Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проводящей через вер­шину конуса. Так, например, чтобы получить действительную длину отрезка S2, надо из 2‘ про­вести горизонтальную прямую до пересечения в точке Ь’ с контурной образующей конуса, являю­щейся действительной ее длиной.

К развертке конической поверхности пристраивают фигуры сечения и основания конуса.

Построение изометрической проекции усечен­ного конуса (рис. 182, в) начинают с построения основания—эллипса. Изометрическую проекцию любой точки кривой сечения находят с помощью трех координат, как показано на рис. 182, в.

На оси х откладывают точки I…VII, взятые с горизонтальной проекции конуса. Из полученных точек проводят вертикальные прямые, на которых откладывают координаты z, взятые с фронтальной проекции. Через полученные на наклонной оси эллипса точки проводят прямые, параллельные оси у, и на них откладывают отрезки 6₀8₀ и 4₀10_0, взятые на действительном виде сечения.

Найденные точки соединяют по лекалу. Край­ние очерковые образующие проводят по каса­тельной к контуру основания конуса и эллипса.

Пример сечения прямого кругового конуса при­веден на рис. 182, г. Колпак сепаратора представ­ляет собой сварную конструкцию из тонкой лис­товой стали и состоит из двух конусов.

Развертка сферической поверхности

Горизонтальную проекцию сферической поверхности делим горизонтально-проецирующими плоскостями на несколько равных частей (клинь­ев), например на 12 (рис. 183, а). Фронтальную проекцию сферы поверхности тоже делят на не­сколько равных частей (желательно на 12).

Через полученные точки деления II. VI прово­дят фронтально- проецирующие плоскости Р_V1… Р_V5 (рис. 183, а).

Для построения развертки сферической повер­хности на горизонтальной прямой откладывают длину окружности диаметра D, равную πD (рис. 183, б). Полученный отрезок делят на 12 равных частей.

Через середину каждого деления проводят пер­пендикуляр и откладывают на нем отрезок I—VII, равный 0.5 длине окружности диаметра D. Отрезок I—VII делят на 6 равных частей, через полу­ченные точки деления проводят горизонтальные прямые, на которых откладывают отрезки, равные 1/12 части окружности соответствующего радиуса, например, отрезок с₁с₂ соответствует 1/12 длине окружности радиуса I—II, взятого с горизонталь­ной проекции. Полученные точки соединяют по лекалу. Развертки остальных одиннадцати клинь­ев строят аналогично.

На рис. 184 и 185 приведены примеры исполь­зования развертки сферической поверхности.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник