Что такое сегмент окружности
Что такое сегмент окружности
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
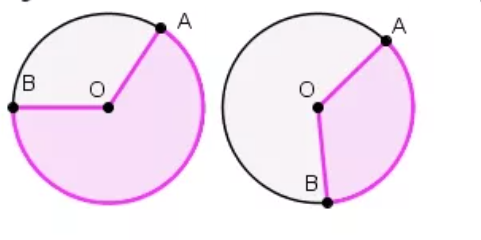
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
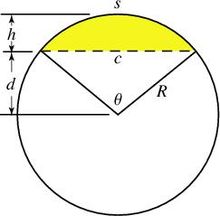
Нахождение площади сегмента круга
В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора). Также разберем примеры решения задач для демонстрации практического применения формул.
Определение сегмента круга
Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.
Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.
Формулы нахождения площади кругового сегмента
Через радиус и центральный угол в градусах
α° – угол в градусах.
Через радиус и угол сектора в радианах
αрад – угол в радианах.
Примеры задачи
Задание 1
Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.
Решение
Воспользуемся первой формулой, подставив в нее известные значения:
Решение
В данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:
Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
На рисунке центр окружности обозначен точкой О. 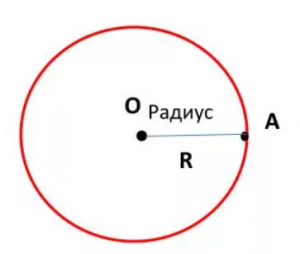
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.
Свойство хорд
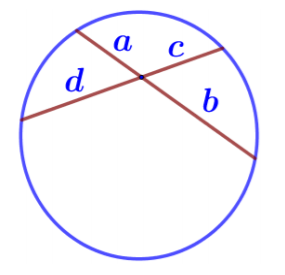
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.
Дуга, касательная, круг, сектор, сегмент
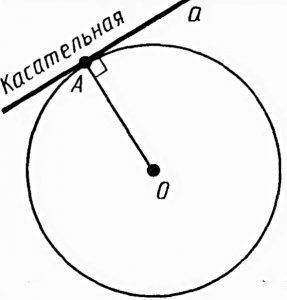
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
Свойства касательной
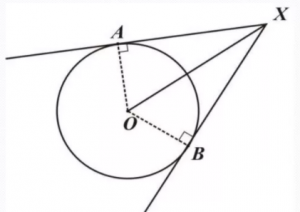
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
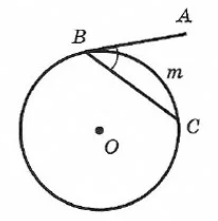
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
Сектор и его площадь
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
Площадь кругового сектора вычисляется по формуле:
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Теорема 4:
Равные хорды стягивают равные дуги.
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Сегмент (геометрия)
Сегмент — плоская фигура, заключённая между кривой и её хордой. Как частный случай, круговой сегмент: часть круга, ограниченная дугой окружности и её хордой или секущей.
Площадь кругового сегмента вычисляется по формуле:
где 
См. также
Полезное
Смотреть что такое «Сегмент (геометрия)» в других словарях:
Сегмент — (от лат. segmentum отрезок, полоса, от seco режу, рассекаю) часть чего либо. В математике Сегмент, или отрезок множество точек прямой, включающее свои концы. Сегмент (геометрия) плоская фигура, заключённая между … Википедия
Сектор (геометрия) — У этого термина существуют и другие значения, см. Сектор. Сектор круга закрашен зелёным Сектор в геометрии часть круга, ограниченная дугой и двумя ра … Википедия
НЕЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера
Жёсткость (геометрия) — У этого термина существуют и другие значения, см. Жёсткость (значения). Жёсткость свойство подмногообразия в евклидовом пространстве (или, более обще, в пространстве постоянной кривизны), заключающееся в том, что любая его изометрическая… … Википедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
Жесткость (геометрия) — Жёсткость свойство подмногообразия M в евклидовом пространстве (или, более обще, в пространстве постоянной кривизны), заключающееся в том, что любая его изометрическая вариация (бесконечно малое изгибание) является тривиальной, то есть… … Википедия
История математики — История науки … Википедия
Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия
Ford C-Max — Ford C Max … Википедия
Вавилонская математика — Данная статья часть обзора История математики. Вавилонская табличка с вычислением = 1.41421296. Вавилоняне писали … Википедия